К вопросу об эксперименте Эйнштейна – де Гааза 4 страница
Макроскопическая работа:
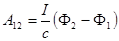 .
.
Работа, совершаемая магнитным полем над током 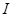 , равна приращению магнитного потока, умноженному на
, равна приращению магнитного потока, умноженному на 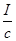 ( в СИ-на I)
( в СИ-на I)
Полученный результат справедлив при любом направлении магнитного поля.
Разложим поле на три составляющие: 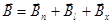 (
( 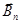 - производит работу, которую мы вычислили;
- производит работу, которую мы вычислили; 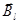 - параллельна току и не оказывает силового воздействия на мостик;
- параллельна току и не оказывает силового воздействия на мостик; 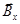 - создает силу, перпендикулярную перемещению, значит
- создает силу, перпендикулярную перемещению, значит 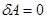 ).
).
Общий случай. Некоторый контур с током 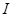 - величина тока не меняется в любом сечении проводника. Контур произвольно перемещается, это может быть связано с деформацией контура.
- величина тока не меняется в любом сечении проводника. Контур произвольно перемещается, это может быть связано с деформацией контура.
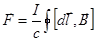 .
.
При перемещении контура на некоторую величину 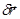 :
:
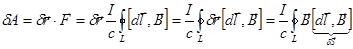 , где
, где 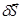 - элемент площади, описываемой контуром при его перемещении .
- элемент площади, описываемой контуром при его перемещении .
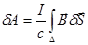 (интеграл – это поток вектора
(интеграл – это поток вектора 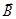 через изменение площади
через изменение площади 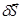 ).
).
Обозначаем: 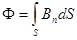 - магнитный поток через произвольную поверхность
- магнитный поток через произвольную поверхность 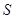 , опирающуюся на контур
, опирающуюся на контур 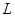 .
.
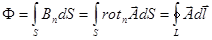 (по теореме Стокса).
(по теореме Стокса).
Магнитный поток через произвольную поверхность 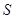 равен циркуляции вектор - потенциала по контуру, на который опирается
равен циркуляции вектор - потенциала по контуру, на который опирается 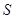 .
.
Работа, которую совершает магнитное поле над контуром с током, определяется изменением магнитного потока через этот контур.
22 ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
Фарадей (1831 г.):
При движении проволочного контура в постоянном магнитном поле в нем возбуждается электрический ток, прекращающийся, когда катушка останавливается.
Этот ток называется индукционным током, а само явление – электромагнитной индукцией.
Индукционный ток в проволочном контуре возникает при любом способе изменения магнитного потока через контур. Направление индукционного тока в контуре определяется правилом Ленца.
Э. Х. Ленц (1804 – 1865) – русский физик и электротехник, академик Петербургской академии наук (1830), ректор Санкт-Петербургского университета (с 1963).
Индукционный ток во всех случаях направлен таким образом, что его действие противоположно действию причины, вызвавшей этот ток.
Например, в замкнутом контуре направление индукционного тока таково, что 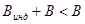 .
.
При размыкании цепи индукционный ток складывается с исходным: лампочка вспыхивает ярко; при замыкании цепи – вычитается: лампочка сначала горит тускло, затем накал нормализуется.
 |
РИС.22-1
Возбуждение тока при движении замкнутого проводящего контура во внешнем магнитном поле объясняется действием силы Лоренца.
 |
РИС.22-2
Проводник, замыкающий металлический контур, движется со скоростью 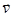 в постоянном магнитном поле
в постоянном магнитном поле 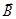 .
.
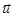 - дрейфовая скорость одного из электронов,
- дрейфовая скорость одного из электронов,
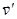 - скорость электрона относительно лабораторной системы отсчета:
- скорость электрона относительно лабораторной системы отсчета: 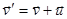 .
.
На электрон действует сила Лоренца:
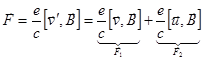
{ 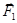 может ускорять электроны вдоль проводника, т.е. может возбуждать электрические токи;
может ускорять электроны вдоль проводника, т.е. может возбуждать электрические токи; 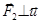 , поэтому дрейфовая скорость не будет меняться.
, поэтому дрейфовая скорость не будет меняться.
 |
(Может наблюдаться только искривление траекторий – эффект Холла)}.
РИС.22-3
На Рис. 22-3 представлен отрезок проводника. Лоренцова сила будет гнать электроны (отрицательно заряженные частицы) влево, техническое направление тока – вправо.
Возникновение индукционного электрического тока в цепи эквивалентно включению в эту цепь некоторого источника сторонней электродвижущей силы, создающего электрическое поле 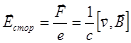 .
.
Сторонняя э.д.с. индукции 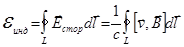 .
.
Воспользуемся векторным тождеством: 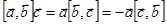 .
.
Отсюда мы сразу получим:
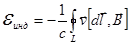 .
.
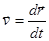 - перемещение некоторого элемента контура на расстояние
- перемещение некоторого элемента контура на расстояние 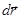 за время
за время 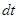 .
.
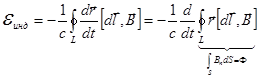 {
{ 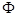 - поток вектора напряженности магнитного поля}.
- поток вектора напряженности магнитного поля}.
Получили 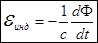 .
.
Э.д.с. индукции равна взятой с обратным знаком скорости изменения потока магнитного вектора через контур проводника.
Если поле 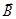 создается током, циркулирующим в контуре
создается током, циркулирующим в контуре 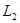 , а контур
, а контур 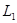 движется равномерно относительно
движется равномерно относительно 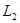 , то индуцированный ток будет равен тому, который будет в контуре
, то индуцированный ток будет равен тому, который будет в контуре 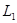 в том случае, если он неподвижен, а
в том случае, если он неподвижен, а 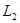 движется со скоростью
движется со скоростью 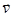 . – Это так, если система отсчета инерциальна и
. – Это так, если система отсчета инерциальна и 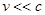 .
.
Если 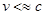 , то нужно пересчитывать по правилам, диктуемым СТО.
, то нужно пересчитывать по правилам, диктуемым СТО.
Обобщение
Э.д.с. индукции 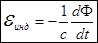 при любом равномерном движении контура
при любом равномерном движении контура  относительно тока
относительно тока 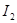 , возбуждающего магнитное поле
, возбуждающего магнитное поле 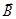 .
.
Опыт показывает также, что формула справедлива
- при неравномерном движении 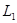 относительно инерциальной системы отсчета с током
относительно инерциальной системы отсчета с током 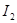 ,
,
- при изменении магнитного потока не только при движении контура 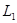 , но и при изменении силы тока в контуре
, но и при изменении силы тока в контуре 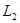 (размыкание-замыкание, переменный ток и т.п.).
(размыкание-замыкание, переменный ток и т.п.).
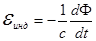 при любом способе изменения магнитного потока.
при любом способе изменения магнитного потока.
Если в контуре имеются какие-то другие источники э.д.с. 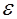 , то сила тока
, то сила тока 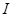 в контуре:
в контуре:
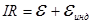 ;
; 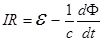 (знак «-», так как индуцированное поле стремится удержать постоянной величину магнитного потока).
(знак «-», так как индуцированное поле стремится удержать постоянной величину магнитного потока).
Максвелловская трактовка электромагнитной индукции
Когда проводник движется в постоянном магнитном поле, индукционный ток вызывается силой Лоренца 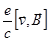 . Какая же сила возбуждает индукционный ток в неподвижном проводнике, находящемся в переменном магнитном поле?
. Какая же сила возбуждает индукционный ток в неподвижном проводнике, находящемся в переменном магнитном поле?
Максвелл: всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле.
Углубленная трактовка закона электромагнитной индукции
Следует говорить о возбуждении электрического поля. Тогда, вспоминая, что
э.д.с.= 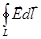 , мы запишем:
, мы запишем:
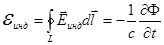 (частная производная, чтобы учесть неоднородное магнитное поле).
(частная производная, чтобы учесть неоднородное магнитное поле).
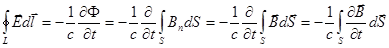 .
.
По теореме Стокса: 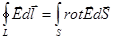 .
.
Приравнивая, находим:
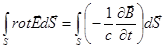 .
.
В силу произвольности поверхности 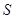 , опирающейся на контур
, опирающейся на контур 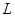 ,
,
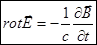 - уравнение Максвелла (2).
- уравнение Максвелла (2).
Это дифференциальная форма закона электромагнитной индукции; уравнение Максвелла (2).
Электрическое поле, возбуждаемое переменным магнитным полем, не является потенциальным, 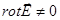 , это вихревое поле.
, это вихревое поле.
Вообще говоря, если проводник движется в переменном магнитном поле, то индукционный ток возбуждается как электрической составляющей, так и магнитной составляющей силы Лоренца:
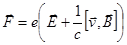 .
.
Какая часть индукционного тока связана с 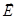 , какая с
, какая с 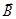 - зависит от выбора системы отсчета (мы об этом уже говорили): можно найти такую систему отсчета, в которой или электрическая, или магнитная составляющая силы Лоренца равна нулю. Могут быть некоторые ситуации, когда это сделать невозможно, так как скорость движения системы отсчета окажется
- зависит от выбора системы отсчета (мы об этом уже говорили): можно найти такую систему отсчета, в которой или электрическая, или магнитная составляющая силы Лоренца равна нулю. Могут быть некоторые ситуации, когда это сделать невозможно, так как скорость движения системы отсчета окажется 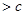 , что противоречит СТО.
, что противоречит СТО.
В движущейся системе отсчета
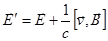 ,
,
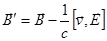 .
.
С какой скоростью нужно двигать систему 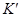 , чтобы поле в этой системе было чисто электрическим?
, чтобы поле в этой системе было чисто электрическим?
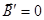 Þ
Þ 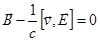 {в векторное произведение входит лишь компонента скорости
{в векторное произведение входит лишь компонента скорости 
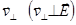 , компонента
, компонента 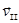 вклада не дает и остается неопределенной величиной}.
вклада не дает и остается неопределенной величиной}.
Итак: 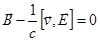 . Умножим слева векторно на
. Умножим слева векторно на 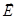 :
: 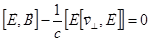 .
.
Двойное векторное произведение раскроем по правилу «бац минус цаб»:
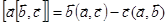 ,
,
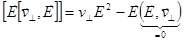 .
.
Отсюда получаем:
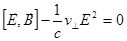 .
.
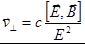
Если система  движется со скоростью
движется со скоростью 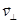 , то поле в этой системе не имеет магнитной составляющей.
, то поле в этой системе не имеет магнитной составляющей.
Дата добавления: 2016-02-24; просмотров: 729;
