К вопросу об эксперименте Эйнштейна – де Гааза 3 страница
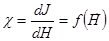 ;
; 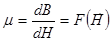 .
.
Природа сил взаимодействия между атомами ферромагнетика установлена в 1927 г.
Я.И. Френкелем и В. Гейзенбергом (Хайзенберг) -нобелевский лауреат 1932 г., на основе квантовой теории: это так называемые обменные силы, эти силы короткодействующие – действуют на расстояниях порядка атомных.
Ферромагнетик в целом – не намагничен при 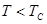 : ферромагнетик представляет собой конгломерат малых, но макроскопических областей (доменов), каждая из которых спонтанно намагничена, но тело в целом - нет, так как суммарные
: ферромагнетик представляет собой конгломерат малых, но макроскопических областей (доменов), каждая из которых спонтанно намагничена, но тело в целом - нет, так как суммарные 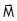 каждой из областей расположены хаотически в пространстве.
каждой из областей расположены хаотически в пространстве.
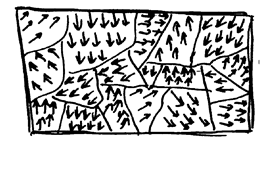 |
Домены:
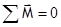 .
.
РИС.21-1
Границы доменов выявляются с помощью магнитного порошка Fe2O3 – оседает на границах, где максимальная неоднородность  .
.
Распад ферромагнетика на домены энергетически выгоден.
Если бы весь ферромагнетик был намагничен в одном направлении, то наблюдался бы минимум энергии обменного взаимодействия. При этом была бы достаточно большая энергия возбуждаемого им магнитного поля. При дроблении на домены магнитное поле, возбуждаемое ферромагнетиком, ослабляется. Уменьшается и соответствующая ему энергия. Энергия обменного взаимодействия (так как она обусловлена короткодействующими силами) не меняется, но только возрастает обменная энергия атомов, расположенных на границах, т.е. поверхностная энергия, пропорциональная полной площади поверхности границ доменов. Чем больше доменов, тем больше поверхностная энергия.
Размер доменов определяется условием
(обменная энергия)+(магнитная энергия)+(поверхностная энергия)=min.
Доказательство доменов - эффект Баркгаузена (1919 г.)
 |
РИС.21-2
Проявляется в виде скачков намагниченности при изменении магнитной индукции. Объясняется изменением границ доменов в магнитомягких материалах. Эффект дал размер доменов: 10-1-10-2см, объем 10-3-10-6см3.
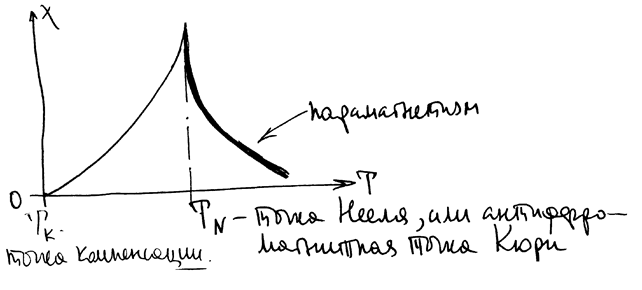 |
Антиферромагнетик: антипараллельная ориентация спинов соседних атомов (MnO, FeF2, Cr2O3 и др.). Две спиновые подрешетки, вставленные одна в другую. Если величина намагничения обеих подрешеток одинакова, то кристалл в целом не обладает магнитным моментом: антиферромагнетизм.
РИС.21-3
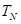 - точка Нееля, или антиферромагнитная точка Кюри.
- точка Нееля, или антиферромагнитная точка Кюри.
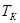 - точка компенсации.
- точка компенсации.
Ферримагнетизм–нескомпенсированный антиферромагнетизм. 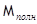 может быть значительным. По магнитным свойствам ферримагнетики аналогичны ферромагнетикам. Если ферримагнетик обладает еще и полупроводниковыми свойствами, то называется ферритом.
может быть значительным. По магнитным свойствам ферримагнетики аналогичны ферромагнетикам. Если ферримагнетик обладает еще и полупроводниковыми свойствами, то называется ферритом.
Краткие итоги: характерные особенности ферромагнетиков:
- нелинейная, неоднозначная связь 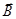 и
и 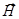 (при
(при 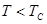 ),
),
- наличие спонтанной намагниченности (при 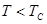 ),
),
- превращение их в парамагнетики при температуре ( 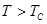 ).
).
Они объясняются на основе модели Вейсса (1907 г.) (с учетом показанного Я.И. Френкелем и В. Гейзенбергом сугубо квантового характера сил взаимодействия), основанной на спонтанном упорядочении ориентации элементарных магнитиков (несущих собственный, спиновый, магнитный момент электрона), так что при 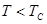 система является упорядоченной, а при
система является упорядоченной, а при 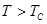 , когда энергии теплового движения атомов
, когда энергии теплового движения атомов 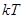 оказывается достаточно, чтобы разбросать магнитики, ферромагнетик превращается в парамагнетик (магнитное состояние неупорядоченное).
оказывается достаточно, чтобы разбросать магнитики, ферромагнетик превращается в парамагнетик (магнитное состояние неупорядоченное).
Отсутствие спонтанной намагниченности макроскопических ферромагнетиков объясняется существованием малых, но макроскопических областей – так называемых доменов – спонтанно намагниченных. Размеры доменов определяются из условия минимума полной энергии:
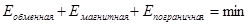 .
.
Размеры доменов 10-1-10-2см (объем 10-3-10-6см3).
Объяснение диамагнетизма ( 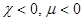 )
)
Наблюдается в веществах, атомы которых в отсутствие внешнего магнитного поля не обладают собственным магнитным моментом: орбитальные и собственные магнитные моменты электронов скомпенсированы, 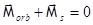 .
.
Между ядром и электронами действуют лишь кулоновские силы притяжения:
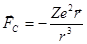 . Z – заряд ядра.
. Z – заряд ядра.
Включаем постоянное магнитное поле 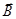 .
.
На электрон будет действовать дополнительно сила Лоренца:
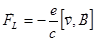 , где
, где 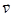 - скорость движения электрона.
- скорость движения электрона.
Следовало бы решать эту задачу квантовым способом, так как речь идет об электроне. Сейчас это невозможно, поэтому предлагается классический подход.
Определим, как изменится движение атома в стационарном состоянии.
Рассмотрим движение в системе отсчета, равномерно вращающейся с угловой скоростью 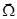 вокруг направления магнитного поля
вокруг направления магнитного поля 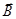 .
. 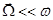 , где
, где 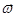 - угловая скорость вращения электрона вокруг ядра.
- угловая скорость вращения электрона вокруг ядра.
Во вращающейся системе отсчета к кулоновской силе и к силе Лоренца добавляются еще две: кориолисова сила 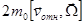 и центробежная сила, которой пренебрегаем, так как она ~
и центробежная сила, которой пренебрегаем, так как она ~ 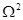 .
.
В выражении для силы Кориолиса относительную скорость электрона 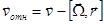 заменим опять же на его абсолютную скорость, так как при этом ошибка будет ~
заменим опять же на его абсолютную скорость, так как при этом ошибка будет ~ 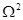 (изменение силы Кориолиса).
(изменение силы Кориолиса).
В состоянии равновесия сила Лоренца должна быть уравновешена силой Кориолиса:
 ,
, 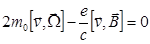 .
.
Равновесие реализуется лишь в том случае, если электронная система атома в целом приобретает угловое вращение с угловой скоростью:
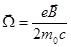 .
.
Теорема Лармора.
При наличии постоянного внешнего магнитного поля 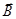 внутреннее движение электронов в атоме не изменяется, но электронная подсистема атома в целом получает дополнительное вращение с угловой скоростью
внутреннее движение электронов в атоме не изменяется, но электронная подсистема атома в целом получает дополнительное вращение с угловой скоростью 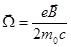 .
.
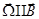 , но заряд электрона
, но заряд электрона 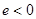 , поэтому магнитный момент, возникающий при ларморовой прецессии,
, поэтому магнитный момент, возникающий при ларморовой прецессии, 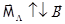 , значит
, значит 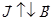 , т.е. диамагнетизм.
, т.е. диамагнетизм.
Дж. Лармор (1857-1942) – английский физик, член (с 1892 г.), секретарь (1901-1912), вице-президент (1912-1914) Лондонского Королевского общества. Окончил Кембриджский университет в 1879 г. В 1903 г. получил кафедру в Кембридже. Научные труды – по электронной теории, электродинамике движущихся сред и математической физике.
Ларморова прецессия – дополнительное вращение как целого (прецессия) устойчивой системы одинаковых заряженных частиц, например, электронов атома, возникающее при наложении на систему однородного постоянного магнитного поля, направление которого и служит осью вращения.
Согласно теореме Лармора при наложении однородного внешнего магнитного поля 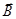 уравнения движения электронов сохраняют свою форму, если перейти к системе координат, равномерно вращающейся вокруг направления поля с угловой частотой
уравнения движения электронов сохраняют свою форму, если перейти к системе координат, равномерно вращающейся вокруг направления поля с угловой частотой 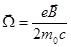 .
.
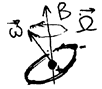 |
На языке полуклассической теории Бора: магнитное поле вызывает прецессию орбиты каждого электрона с частотой
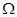 вокруг направления поля.
вокруг направления поля.
РИС.21-4
Теорема Лармора верна, если 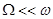 , где
, где 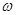 - собственная частота обращения частиц в отсутствие магнитного поля.
- собственная частота обращения частиц в отсутствие магнитного поля.
Для электронов при 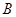 ~106 Э
~106 Э 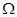 ~1013с-1, тогда как
~1013с-1, тогда как 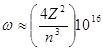 с-1, где
с-1, где 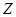 - заряд ядра,
- заряд ядра, 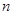 - главное квантовое число.
- главное квантовое число.
Теорема Лармора имеет очень широкую область применимости.
В результате дополнительного вращения системы электронов в магнитном поле возникает магнитный момент системы.
На основе представлений о ларморовой прецессии можно объяснить следующие явления:
- диамагнетизм,
- нормальный эффект Зеемана,
- магнитное вращение плоскости поляризации (эффект Фарадея).
Расчет магнитной восприимчивости диамагнетика
Момент количества движения электрона, вращающегося с угловой скоростью 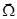 по окружности радиуса
по окружности радиуса 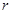 :
: 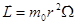 .
.
Его магнитный момент (с учетом 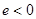 ):
):
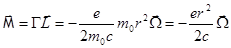 .
.
Подставляем 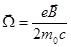 .
.
Тогда 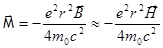 .
.
Чтобы найти магнитный момент атома, надо просуммировать магнитные моменты всех его электронов; если электронов 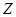 , то
, то
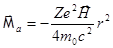 (
( 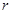 - нужно усреднить расстояние от ядра).
- нужно усреднить расстояние от ядра).
В диамагнетиках электроны в атомах (молекулах) расположены сферически симметрично, т.е.: 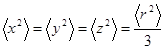 .
.
Если магнитное поле направлено по оси  , то
, то
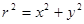
и средний магнитный момент атома:
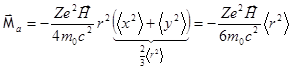 .
.
Вектор намагничивания среды:
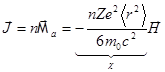 .
.
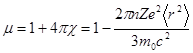 .
.
Поскольку энергия теплового движения мала и не может изменить внутреннее (квантованное) состояние атома, то в диамагнетиках 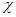 и
и 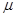 не должны зависеть от температуры, что и наблюдается на опыте.
не должны зависеть от температуры, что и наблюдается на опыте.
Видно также из формулы, что, измерив 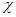 или
или 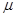 , можно определить величину
, можно определить величину 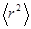 ,
, 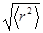 порядка размеров атома. Полученные таким способом значения согласуются с данными, полученными другими методами. Например для He r~0.63 Å, Ar r~0.67 Å.
порядка размеров атома. Полученные таким способом значения согласуются с данными, полученными другими методами. Например для He r~0.63 Å, Ar r~0.67 Å.
Примечание
Ларморовская прецессия возникает в момент включения внешнего магнитного поля и связана она с явлением электромагнитной индукции. Как следует из правила Ленца (реакция системы всегда направлена так, чтобы препятствовать внешнему воздействию), индуцированное магнитное поле 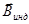 должно препятствовать всякому изменению внешнего магнитного поля
должно препятствовать всякому изменению внешнего магнитного поля 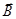 . Следовательно, диамагнетизм универсален, существует всегда. Однако он перекрывается во многих случаях более сильными эффектами – парамагнетизмом и ферромагнетизмом.
. Следовательно, диамагнетизм универсален, существует всегда. Однако он перекрывается во многих случаях более сильными эффектами – парамагнетизмом и ферромагнетизмом.
Объяснение парамагнетизма ( 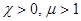 )
)
Парамагнетизм наблюдается у тех веществ, атомы (молекулы) которых обладают магнитными моментами в отсутствие внешнего магнитного поля.
Нет внешнего поля – атомы совершают беспорядочное тепловое движение, их магнитные моменты ориентированы в пространстве беспорядочно, тело не намагничено.
Включено поле – магнитные моменты ориентируются преимущественно в направлении поля: появляется намагничение и обусловленный им парамагнетизм.
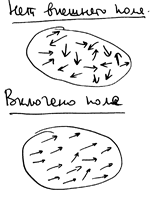 |
РИС.21-5
Излагаемая ниже теория парамагнетизма разработана Ланжевеном применительно к телам, для которых существенно мало взаимодействие между атомами: газы, жидкости или кристаллы, электронные оболочки атомов у которых более или менее свободно вращаются вокруг ядер (это атомы благородных газов или ионные кристаллы с полностью заполненными внешними электронными оболочками, электронные оболочки должны обладать сферической симметрией).
Классическое, т.е. неквантовое приближение
Рассмотрим поведение изолированного атома в магнитном поле 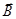 . Допустим, что магнетизм сугубо орбитальный (спины скомпенсированы). Пусть
. Допустим, что магнетизм сугубо орбитальный (спины скомпенсированы). Пусть 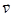 - скорость какого-либо электрона до внесения в магнитное поле.
- скорость какого-либо электрона до внесения в магнитное поле.
Скорость того же электрона в магнитном поле (согласно теореме Лармора): 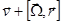 , где
, где 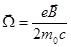 ; его кинетическая энергия:
; его кинетическая энергия: 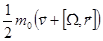 .
.
Пренебрегая квадратичными по 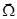 членами, получаем приращение кинетической энергии электрона, обусловленное наличием внешнего поля:
членами, получаем приращение кинетической энергии электрона, обусловленное наличием внешнего поля:
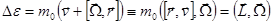 , где
, где 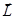 - момент количества движения данного электрона.
- момент количества движения данного электрона.
Эти же соображения можно применить ко всем электронам, тогда нужно полагать: 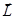 - момент количества движения электронной оболочки.
- момент количества движения электронной оболочки.
Вспоминая, что 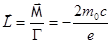 (знак минус-с учетом отрицательного знака заряда электрона),
(знак минус-с учетом отрицательного знака заряда электрона),
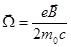 , получаем
, получаем 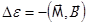 .
.
Такое же изменение энергии, но уже потенциальной, мы получили бы для витка с током, создающим магнитный момент 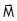 при внесении его в магнитное поле напряженностью
при внесении его в магнитное поле напряженностью 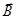 .
.
{ Аналогия 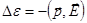 .}
.}
Эта формула 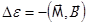 справедлива независимо от того, чем обусловлен магнитный момент, справедлива и для спиновых магнитных моментов.
справедлива независимо от того, чем обусловлен магнитный момент, справедлива и для спиновых магнитных моментов.
Классическая теория парамагнетизма не отличается от теории поляризации полярных диэлектриков Дебая, которую мы изучали раньше. Однако теория парамагнетизма была создана Ланжевеном раньше, чем теория поляризации диэлектриков, которая по сути копирует теорию Ланжевена.
Поль Ланжевен (1872-1946) – французский физик и общественный деятель, член Парижской АН (1934), почетный член АН СССР (1929), член Лондонского Королевского общества.
Как видно из формулы 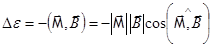 , энергия минимальна, когда
, энергия минимальна, когда 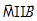 .
.
Поэтому в состоянии статистического равновесия больше моментов будет ориентировано по полю, чем в противоположном направлении, т.е. будет наблюдаться парамагнетизм.
Если выполнено условие 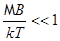 , то по аналогии с теорией поляризации диэлектриков можем сразу записать:
, то по аналогии с теорией поляризации диэлектриков можем сразу записать:
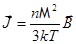 .
.
Воспользуемся соотношениями 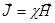 ,
, 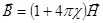 :
:
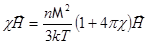 Þ
Þ 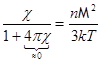 Þ
Þ
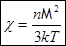
(обратно пропорционально температуре – закон Кюри).
В случае сильных магнитных полей или низких температур, когда условие 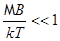 не выполняется, намагничение парамагнетика задается соотношением
не выполняется, намагничение парамагнетика задается соотношением 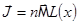 , где
, где 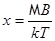 ,
,  - функция Ланжевена.
- функция Ланжевена.
Если  , то
, то 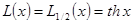 .
.
 |
В классическом пределе, когда возможны все ориентации магнитного момента,
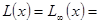 cthx – 1/x
cthx – 1/x
При 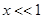
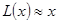 , что и было получено ранее.
, что и было получено ранее.
РИС.21-6
Краткие итоги
Разобрались со свойствами магнетиков.
Особенности сильномагнитныхвеществ (нелинейная, неоднозначная связь 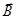 и
и 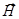 и наличие спонтанной намагниченности при
и наличие спонтанной намагниченности при 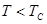 , превращение в парамагнетик при
, превращение в парамагнетик при 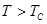 ) объясняются на основе модели Вейсса (1907 г.): ориентационная упорядоченность элементарных магнитиков (собственных) под действием сил обменного взаимодействия. Образование доменов объясняет отсутствие намагниченности макроскопических образцов. Размеры доменов определяются из условия минимума полной энергии ферромагнетика.
) объясняются на основе модели Вейсса (1907 г.): ориентационная упорядоченность элементарных магнитиков (собственных) под действием сил обменного взаимодействия. Образование доменов объясняет отсутствие намагниченности макроскопических образцов. Размеры доменов определяются из условия минимума полной энергии ферромагнетика.
В слабомагнитных веществах – диамагнетиках и парамагнетиках:
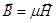 ;
; 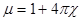 ;
; 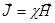 - связь намагниченности (или магнитного поля) со вспомогательным вектором
- связь намагниченности (или магнитного поля) со вспомогательным вектором 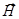 линейная, однозначная.
линейная, однозначная.
Диамагнетиками ( 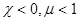 ) являются вещества, атомы (молекулы) которых не имеют собственного (нескомпенсированного) магнитного момента, т.е.
) являются вещества, атомы (молекулы) которых не имеют собственного (нескомпенсированного) магнитного момента, т.е. 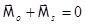 .
.
Во внешнем магнитном поле 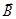 возникает прецессия электронного облака (электронной подсистемы) с ларморовой частотой
возникает прецессия электронного облака (электронной подсистемы) с ларморовой частотой 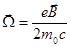 , в результате чего возникает магнетизм
, в результате чего возникает магнетизм 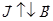 . Поскольку ни внешнее поле (пока и поскольку
. Поскольку ни внешнее поле (пока и поскольку 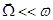 ), ни температура не могут изменить внутреннюю электронную структуру атома, диамагнетизм от температуры не зависит:
), ни температура не могут изменить внутреннюю электронную структуру атома, диамагнетизм от температуры не зависит:
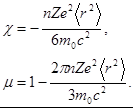
Одним из ярких доказательств справедливости данной теории диамагнетизма является совпадение средних размеров атома, определенных по измерениям магнитной восприимчивости (благородных газов, к которым наиболее полно применима данная теория), как с результатами, полученными другими методами, так и с теоретическими оценками.
Парамагнитными ( 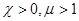 ) являются вещества, атомы (молекулы) которых обладают собственным (нескомпенсированным) магнитным моментом в отсутствие внешнего магнитного поля. Теория намагниченности парамагнетиков (П. Ланжевен) вполне аналогична теории поляризации полярных диэлектриков (П. Дебай).
) являются вещества, атомы (молекулы) которых обладают собственным (нескомпенсированным) магнитным моментом в отсутствие внешнего магнитного поля. Теория намагниченности парамагнетиков (П. Ланжевен) вполне аналогична теории поляризации полярных диэлектриков (П. Дебай).
В области слабых магнитных полей или достаточно высоких температур, когда выполняется условие 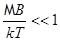 , получаем {поскольку энергия магнитного момента
, получаем {поскольку энергия магнитного момента 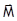 во внешнем магнитном поле
во внешнем магнитном поле 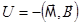 и, следовательно, минимальна, когда
и, следовательно, минимальна, когда 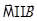 }
}
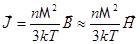 , т.е.
, т.е.
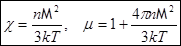
Если условие 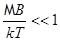 не выполняется (слишком низкие температуры, сильные поля), то
не выполняется (слишком низкие температуры, сильные поля), то 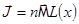 , где
, где 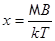 .
.
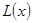 - функция Ланжевена; при
- функция Ланжевена; при 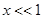
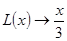 , что и было получено раньше.
, что и было получено раньше.
Диамагнетизм имеет общий характер, так как согласно правилу Ленца система реагирует на внешнее воздействие, чтобы уменьшить влияние этого воздействия на систему.
Однако слабый диамагнетизм перекрывается, как правило, более сильными эффектами – парамагнетизмом и ферромагнетизмом.
 |
Работа при перемещении витка с током в магнитном поле
РИС.21-7
Рассматриваем частный случай: параллельные провода, однородное поле 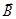 направлено на нас; проводящий мостик
направлено на нас; проводящий мостик 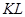 замыкает ток
замыкает ток 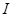 , текущий по проводам левее мостика.
, текущий по проводам левее мостика.
Магнитное поле действует на мостик с силой
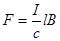 {Закон Ампера:
{Закон Ампера: 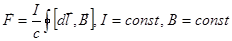 .}
.}
При перемещении мостика на расстояние 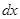 эта сила совершает работу:
эта сила совершает работу:
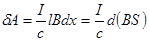 ;
;
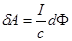 {
{ 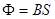 - поток магнитного поля через площадку
- поток магнитного поля через площадку 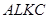 ,
,
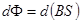 - изменение магнитного потока при перемещении на
- изменение магнитного потока при перемещении на 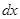 }.
}.
Дата добавления: 2016-02-24; просмотров: 680;
