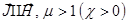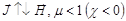К вопросу об эксперименте Эйнштейна – де Гааза 2 страница
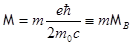 , где
, где 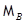 =9.27×10-21 эрг/Гс=5.78×10-13 эВ/Гс - магнетон Бора,
=9.27×10-21 эрг/Гс=5.78×10-13 эВ/Гс - магнетон Бора,
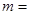 0,±1,±2…. – магнитное квантовое число.
0,±1,±2…. – магнитное квантовое число.
Магнитное квантовое число может принимать те или иные значения в зависимости от состояния, в котором находится атом, однако величина магнитного момента всегда будет целым кратным магнетона Бора.
Проекция механического момента на некоторое выделенное направление (ось 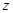 ):
):
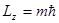 (где
(где 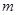 - то же самое магнитное квантовое число).
- то же самое магнитное квантовое число).
Отношение орбитального магнитного момента к механическому:
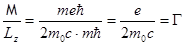 - гиромагнитное отношение; это универсальная постоянная, которую можно измерить.
- гиромагнитное отношение; это универсальная постоянная, которую можно измерить.
Как будет показано в квантовой физике, если атом находится в основном состоянии (наинизшем по энергии) 1S, то магнитное квантовое число может иметь только одно значение 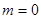 . Следовательно, магнитный момент атома в основном состоянии =0.
. Следовательно, магнитный момент атома в основном состоянии =0.
Опыт Штерна и Герлаха (1921 год)
(Определение магнитных моментов атомов и молекул)
Мы установили, что сила, действующая на магнитный диполь, 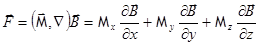 .
.
В однородном магнитном поле эта сила =0.
Чтобы определить величину магнитного момента, нужно пропустить пучок атомов через неоднородное магнитное поле и измерить отклонение. Очевидно, что магнитное поле должно быть неоднородным на расстояниях порядка размеров диполя (иначе будет только поворот в поле).
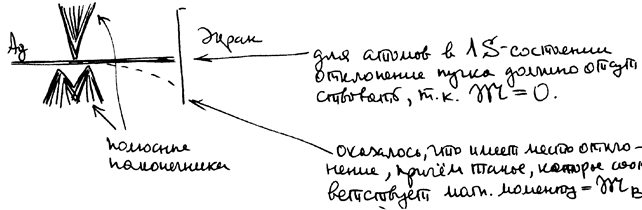
РИС.20-2
Для атомов в 1S-состоянии отклонение пучка на экране должно отсутствовать, так как 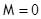 .
.
Оказалось, что имеет место отклонение, причем такое, которое соответствует магнитному моменту, равному 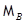 .
.
Собственный механический и магнитный момент электрона
Уленбек и Гаудсмит – спин. Это собственный момент количества движения электрона. Проекция собственного механического момента на произвольное выделенное направление (ось 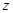 ):
): 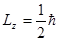 .
.
Получается гиромагнитное отношение другое:
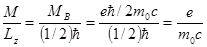 - спиновое гиромагнитное отношение вдвое больше орбитального!
- спиновое гиромагнитное отношение вдвое больше орбитального!
Значит, ели определить гиромагнитное отношение, то можно узнать, каково происхождение магнитного момента в веществе.
Опыт Эйнштейна – де Гааза (1915 г.)
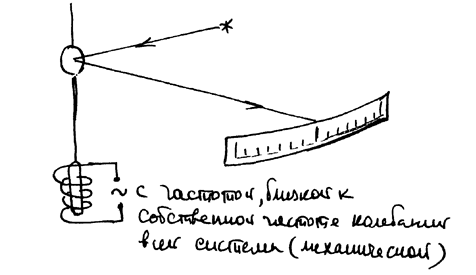 |
Существует жесткая связь между магнитным и механическим моментами. Значит, если мы тело намагнитим, т.е. ориентируем определенным образом магнитные моменты, то ориентируются определенным образом и механические моменты. Поскольку до намагничивания образец в целом момента количества движения не имел, то для выполнения закона сохранения момента количества движения образец должен закрутиться (как целое) в противоположном направлении. Это закручивание можно обнаружить и измерить.
РИС.20-3
Таким образом было установлено, например, что в ферромагнетиках их магнитные свойства обусловлены преимущественно спиновыми моментами (собственными).
Кроме магнитных моментов электронов – орбитальных и собственных (спиновых), вклад в магнитные свойства вещества дают также магнитные моменты ядер, которые, впрочем, много меньше электронных, так как масса ядер велика и скорости движения ядер малы.
Ядерный магнетизм обычно можно (удается) обнаружить лишь при температурах, близких к абсолютному нулю.
Ядерный магнетон Бора: 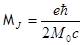 . Для протона масса
. Для протона масса 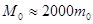 ; следовательно,
; следовательно, 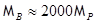 .
.
Итак, магнитные свойства вещества определяются орбитальными и собственными магнитными моментами электронов.
К вопросу об эксперименте Эйнштейна – де Гааза
Магнитный момент одного атома 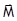 .
.
Момент количества движения одного атома относительно выделенной оси 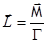 ,
,
где 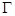 - гиромагнитное отношение.
- гиромагнитное отношение.
В результате намагничения тело в целом приобретет момент 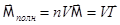 . V-объем.
. V-объем.
Поскольку все эти силы внутренние, то, если тело находилось в покое, оно должно придти во вращение с угловой скоростью 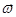 , определяемой из уравнения
, определяемой из уравнения
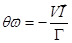 (вращение в обратную сторону).
(вращение в обратную сторону).
Отсюда можно найти 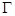 и определить природу магнетизма.
и определить природу магнетизма.
С точки зрения внешнего наблюдателя это соответствует протеканию в веществе токов намагничения.
В отсутствие внешнего магнитного поля – хаотическая ориентация элементарных магнитиков.
Включили поле – вещество намагничивается (упорядочиваются магнитики). Большинство веществ намагничиваются слабо. Сильно – только ферромагнетики. В подавляющем большинстве случаев снятие внешнего магнитного поля приводит к исчезновению намагниченности.
Токи намагничения
Микроскопическое магнитное поле возникает в результате движения элементарных частиц, это движение эквивалентно так называемым молекулярным токам.
Путем усреднения по физически малым объемам можно вычислить макроскопическое поле 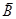 , которое возникает (формально) при протекании по веществу токов намагничения
, которое возникает (формально) при протекании по веществу токов намагничения 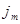 и
и 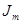 . Обычные токи назовем токами проводимости
. Обычные токи назовем токами проводимости 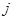 и
и 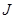 .
.
С учетом сказанного по теореме о циркуляции имеем:
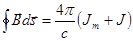 , что эквивалентно дифференциальному уравнению
, что эквивалентно дифференциальному уравнению
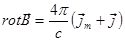 .
.
Этот подход, вообще говоря, - формальный. Обычно используется более физический подход.
Введем вектор намагничивания 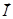 и определим его как сумму магнитных моментов частиц, содержащихся в единице объема:
и определим его как сумму магнитных моментов частиц, содержащихся в единице объема: 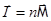 , где
, где 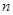 - концентрация частиц, имеющих магнитный момент
- концентрация частиц, имеющих магнитный момент 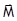 . Будем называть эти частицы молекулами.
. Будем называть эти частицы молекулами.
Теорема о циркуляции магнитного поля в веществе
 |
Мы определили вектор намагничивания
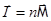 .
.
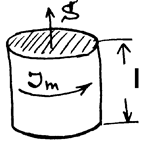
РИС.20-4
Если намагничиваемое нами вещество (магнетик) – это просто цилиндр, объемом 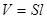 , то полный магнитный момент этого цилиндра =
, то полный магнитный момент этого цилиндра = 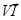 :
: 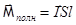 .
.
С другой стороны, такой же точно полный магнитный момент создается током намагничения. Поскольку все токи внутри цилиндра компенсируются взаимно целиком и полностью, остается только ток на поверхности цилиндра:
.
Поскольку вектор 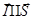 , то
, то 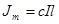 .
.
На единицу длины (высоты) цилиндра приходится ток намагничения 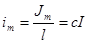 .
.
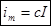 .
.
Для намагничиваемого вещества в произвольном объеме справедливо соотношение:
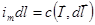 .
.
Полный ток намагничения:
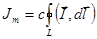 . Здесь
. Здесь 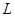 - произвольный замкнутый контур.
- произвольный замкнутый контур.
По теореме о циркуляции имеем:
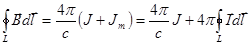 .
.
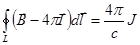 .
.
Дифференциальная форма записи этого соотношения:
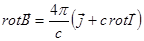 .
.
Сравнивая с уравнением 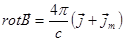 , находим:
, находим: 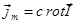 .
.
Если намагниченность однородна, т.е. 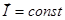 , то
, то 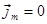 .
.
Если намагниченность неоднородна, т.е. зависит от координат - 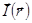 , то объемная плотность тока намагничения
, то объемная плотность тока намагничения 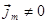 .
.
Введем вспомогательный вектор 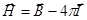 .
.
Получаем: 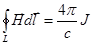 , где
, где 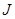 - это только ток проводимости.
- это только ток проводимости.
Дифференциальная форма:
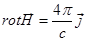 , где
, где 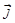 - плотность объемных токов проводимости.
- плотность объемных токов проводимости.
Смысл введения вектора 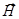 состоит только в том, чтобы убрать из соответствующих уравнений токи намагничивания и оставить только токи проводимости.
состоит только в том, чтобы убрать из соответствующих уравнений токи намагничивания и оставить только токи проводимости.
В учении о магнетизме вектор 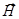 играет такую же вспомогательную роль, что и вектор
играет такую же вспомогательную роль, что и вектор 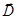 в учении об электростатических полях.
в учении об электростатических полях.
Размерность векторов 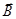 и
и 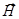 одинакова, в вакууме они тождественно совпадают. Обычно
одинакова, в вакууме они тождественно совпадают. Обычно 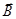 измеряют в Гс (Гаусс), а
измеряют в Гс (Гаусс), а 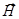 в Э (Эрстед), хотя между этими величинами нет никакой разницы.
в Э (Эрстед), хотя между этими величинами нет никакой разницы.
Граничные условия для векторов 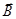 и
и 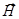
Все магнитные среды делятся на 3 категории:
-парамагнетики – в них вектор намагничивания параллелен внешнему магнитному полю, 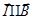 (O2, Al, Pt, FeCl3…);
(O2, Al, Pt, FeCl3…);
-диамагнетики – вектор 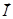 антипараллелен по отношению к внешнему магнитному полю (N2, CO2, H2O, Ag, Bi…);
антипараллелен по отношению к внешнему магнитному полю (N2, CO2, H2O, Ag, Bi…);
-ферромагнетики – сложная связь (нелинейная) между векторами 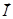 и
и 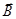 , имеется спонтанная намагниченность, гистерезис (Fe, Ni, Co, различные их сплавы).
, имеется спонтанная намагниченность, гистерезис (Fe, Ni, Co, различные их сплавы).
По историческим причинам пишут связь не между 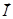 и
и 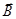 , а между
, а между 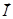 и
и 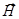 в типичной форме:
в типичной форме: 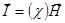 Þ {
Þ { 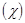 - тензор магнитной восприимчивости} Þ
- тензор магнитной восприимчивости} Þ
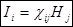 .
.
В приближении изотропной среды 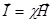 (
( 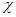 - магнитная восприимчивость).
- магнитная восприимчивость).
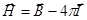 Þ
Þ 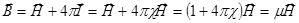 .
.
Магнитная проницаемость 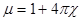 .
.
В парамагнетиках 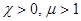 .
.
В диамагнетиках 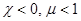 .
.
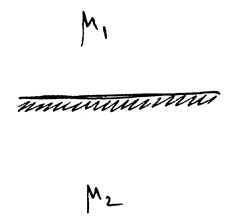 |
Рассмотрим границу раздела двух магнетиков и нормальную компоненту B.
РИС.20-5
Магнитных зарядов не существует, следовательно, 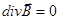 .
.
Отсюда 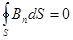 .
. 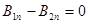 Þ
Þ 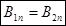 .
.
На границе раздела двух магнетиков нормальная компонента вектора 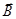 непрерывна.
непрерывна.
Рассмотрим тангенциальную компоненту B.
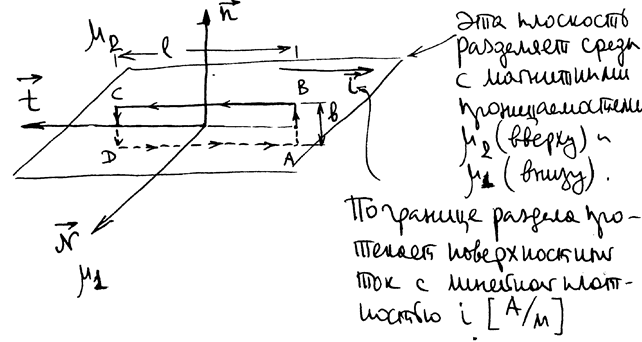
РИС.20-6
Теорему о циркуляции применяем к бесконечно малому прямоугольному контуру 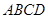
с длиной основания 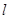 , высота b пренебрежимо мала по сравнению с
, высота b пренебрежимо мала по сравнению с 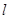 (
( 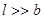 )
)
Пренебрегаем тогда вкладом в циркуляцию сторон 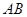 и
и 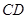 .
.
Циркуляция вектора 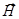 будет:
будет:
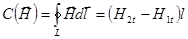 .
.
По теореме о циркуляции эта же величина 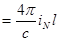 , где
, где 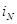 - слагающая поверхностного тока
- слагающая поверхностного тока 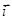 вдоль направления
вдоль направления 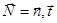 .
.
Приравнивая эти выражения, находим:
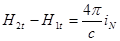 .
.
Это же выражение можно записать в векторной форме.
Правая сторона: 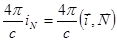 .
.
Левая сторона: 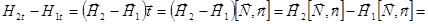
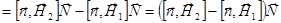 .
.
Приравнивая, находим:
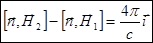 .
.
При отсутствии поверхностных токов (диэлектрические среды): 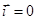 ,
, 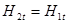 - тангенциальные компоненты вектора
- тангенциальные компоненты вектора 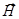 на границе раздела непрерывны.
на границе раздела непрерывны.
По магнитным свойствам все вещества можно разделить на:
|
| |||||||||||||||||||||||||||
 |  |  |  |  | ||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
Основные свойства сильномагнитных веществ:
- только твердые тела;
- необходимо (но недостаточно), чтобы в состав кристаллической решетки входили
атомы с недостроенными внутренними оболочками;
- обладают спонтанной намагниченностью (чем напоминают сегнетоэлектрики);
- сложная, нелинейная зависимость 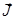 от
от 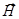 .
.
Ферромагнетиками являются:
Fe, Co, Ni и многие их сплавы,
Gd, Tb, Dy, Ho, Er, Tm – при низких температурах.
Экспериментально (А.Г. Столетов):
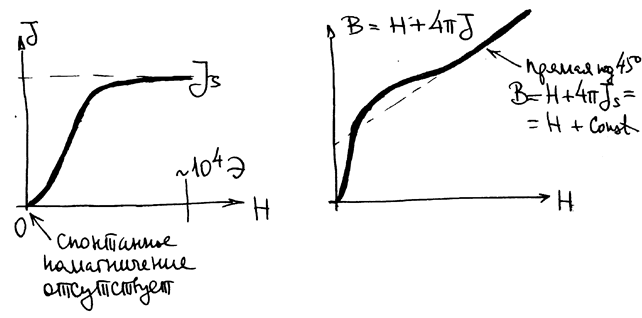
РИС.20-7
Ввиду нелинейной связи между 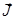 и
и 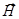 и между
и между 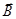 и
и 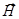 в ферромагнетиках нельзя, вообще говоря, ввести магнитную восприимчивость
в ферромагнетиках нельзя, вообще говоря, ввести магнитную восприимчивость 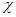 и магнитную проницаемость
и магнитную проницаемость 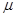 как определенные характеризующие вещество постоянные величины. Можно, конечно, записать
как определенные характеризующие вещество постоянные величины. Можно, конечно, записать 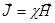 и
и 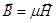 , но
, но 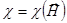 и
и 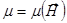 .
.
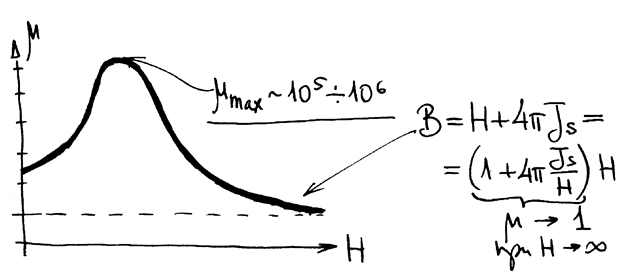
РИС.20-8
На больших значениях 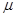 основаны практические применения ферромагнетиков: электромагниты, постоянные магниты для получения полей ~104 Э. Для получения более сильных полей применение ферромагнитных сердечников бессмысленно и вредно (возрастают потери энергии). Сильные и сверхсильные магнитные поля получают с помощью одних только катушек (из меди, сверхпроводников) с током (постоянным или импульсным).
основаны практические применения ферромагнетиков: электромагниты, постоянные магниты для получения полей ~104 Э. Для получения более сильных полей применение ферромагнитных сердечников бессмысленно и вредно (возрастают потери энергии). Сильные и сверхсильные магнитные поля получают с помощью одних только катушек (из меди, сверхпроводников) с током (постоянным или импульсным).
Особенность ферромагнетиков в том, что зависимость 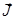 от
от 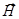 или
или 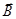 от
от 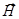 неоднозначна и зависит от предшествующей истории намагничивания образца (гистерезис).
неоднозначна и зависит от предшествующей истории намагничивания образца (гистерезис).
Петля гистерезиса узкая в магнитно-мягких материалах (сердечники для электромагнитов). Для материалов, идущих на изготовление постоянных магнитов, коэрцитивная сила велика, остаточное намагничивание велико, петля гистерезиса – широкая.
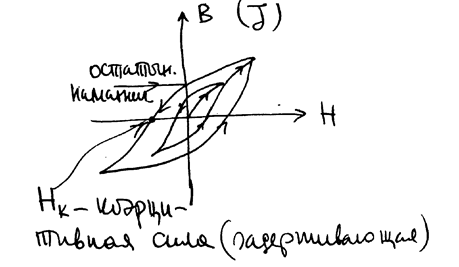 |
РИС.20-9
Вследствие наличия гистерезиса перемагничивание ферромагнетиков сопровождается выделением тепла, называемого теплом гистерезиса.
Для бесконечно малого квазистатического процесса:
тепло гистерезиса 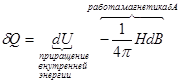 {напомним, что для диэлектрика (плоский конденсатор с диэлектриком)
{напомним, что для диэлектрика (плоский конденсатор с диэлектриком) 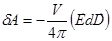 }.
}.
Если проинтегрировать выражение для 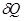 по одному циклу перемагничивания. т.е. по одной петле гистерезиса, получим:
по одному циклу перемагничивания. т.е. по одной петле гистерезиса, получим:
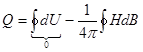 .
.
Видно, что тепло гистерезиса с точностью до 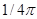 равно площади петли гистерезиса.
равно площади петли гистерезиса.
Пример: Стальной цилиндр нагревается внутри катушки, питаемой переменным током.
Медный – не нагревается.
При некоторой характерной температуре 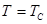 (точка Кюри) ферромагнетик превращается в парамагнетик (
(точка Кюри) ферромагнетик превращается в парамагнетик ( 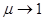 ).
).

РИС.20-10
21 Теория ферромагнетизма
Феноменологически теория ферромагнетизма была развита Вейссом в 1907 г. Он предположил, что атомы ферромагнетика обладают собственным магнитным моментом и взаимодействуют между собой так, чтобы магнитные моменты устанавливались параллельно друг другу. Поскольку ориентация атомов осуществляется внутренними силами, возникает спонтанное намагничение ферромагнетика (при температуре 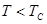 ). Состояние спонтанного намагничения энергетически выгодно. Сначала два магнитных момента выстаиваются параллельно (
). Состояние спонтанного намагничения энергетически выгодно. Сначала два магнитных момента выстаиваются параллельно ( 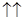 ) из-за флуктуации, затем – остальные. Насыщения не происходит, так как этому препятствует тепловое движение.
) из-за флуктуации, затем – остальные. Насыщения не происходит, так как этому препятствует тепловое движение.
С другой стороны, энергии теплового движения недостаточно для того, чтобы разрушить состояние спонтанного намагничения.
При температурах ниже 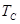 вещество находится в «упорядоченном состоянии», при
вещество находится в «упорядоченном состоянии», при 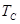 происходит переход в «неупорядоченное состояние», в котором спонтанное намагничение отсутствует.
происходит переход в «неупорядоченное состояние», в котором спонтанное намагничение отсутствует.
При 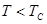 магнитная восприимчивость
магнитная восприимчивость 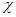 и магнитная проницаемость
и магнитная проницаемость 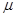 являются функциями магнитного вектора
являются функциями магнитного вектора 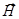 :
:
Дата добавления: 2016-02-24; просмотров: 1152;

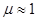
 (только твердые тела)
(только твердые тела)