РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ НА ПРОЛОГЕ
Целью всего предшествующего изложения была подготовка к данному разделу -решению содержательных логических задач на Прологе, т.е. задач невычислительного характера, в которых особенности Пролога и дескриптивной парадигмы программирования проявляются наиболее ярко.
Рассмотрим пример: нарисовать конверт, не отрывая карандаша от бумаги и не проводя два раза по одной и той же линии.
Введем обозначения, как показано на рис. 3.17. Ребра графа обозначены буквами а, б, в ... (литерные константы), вершины - цифрами 1, 2, 3 ... Опишем структуру графа предикатом вида «ребро (S, А, В)», что означает, что от вершины А к вершине В идет ребро S. Так как граф неориентированный, помимо предикатов вида «ребро (S, А, В)» нужны и предикаты «ребро (S, В, А)». Знания о структуре графа можно представить так, как это записано рядом с рис. 3.17.
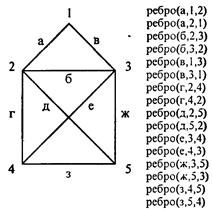
Рис. 3.17. Задача «конверт»
Решением задачи должен явиться список пройденных ребер графа, причем длина его должна быть равна 8 и в нем не должно быть повторяющихся ребер, что можно описать так:
путь(Т,П) : - длина(П,8), write_list(П),!.(1)
путь(Т,П) : - ребро(Р,Т,Н),не_принад(Р,П),путь(Н,[Р|П]).(2)
Переменная Т обозначает текущую вершину графа, а П - список пройденных ребер Правило 1 означает, что если длина списка П пройденных вершин становится равной 8, список П выводится на печать. Это правило ограничивает рекурсивный перебор вершин и ребер, проводимый правилом 2. Правило 2 является генератором перебора, оно перебирает предикаты «ребро()»и находит такое ребро Р из текущей вершины Т в новую Н, чтобы оно не принадлежало списку П, затем это ребро добавляется в качестве головы к списку П, и поиск дальнейшего пути производится уже из новой вершины Н.
Нам потребуется программа, определяющая длину списка,
длина ([],()).
длина ([А | В], N) :- длина (В, М), N is M+1.
а также программа вывода элементов списка на экран
write_list([]).
write_list([H | T]):-write(H),write_list(T).
Задание
?-путь(4,[]).
- искать путь, начиная с вершины 4 и пустого списка пройденных ребер.
Ответ: з, ж, в, а, б, д, г, е.
На вопрос ?-путь(1,[]) ответ-«НЕТ».
Аналогично решаются другие задачи, связанные с поиском пути в графе, удовлетворяющего каким-то дополнительным условиям, например задача о коммивояжере. Программа будет состоять
1) из базы знаний о структуре графа - вершинах и связывающихих ребрах(каждому ребру может сопоставляться набор весов);
2) из правил, выражающих дополнительные условия и ограничения на решения задачи и часто связанных с обработкой списков.
3) из рекурсивного правила - генератора перебора ребер и вершин с некоторым ограничивающим предложением, целевым условием;
4) из дополнительных процедур и промежуточных определений.
Интересно, что большинство задач, которые считаются логическими, сводятся к задаче поиска пути в некотором графе - графе состояний задачи. К этому типу задач можно отнести и разнообразные игры. Характерными особенностями многих задач являются следующие:
1) наличие неких дискретных состояний, число которых конечно, и одноиз них принимается за начальное, а другое (или несколько других) за конечное (искомое);
2) определены правила перехода между состояниями;
3) для каждого состояния заданы определенные условия допустимости (оценки) этого состояния.
При анализе предметной области задачи эти состояния, правила перехода и условия допустимости должны быть выявлены, получены соответствующие обозначения и затем записаны с помощью фраз Хорна.
Рассмотрим задачу: имеются два сосуда - на 3 и на 5 литров. Как отмерить с их помощью 4 литра воды ?
В этой задаче состояния связаны с определенным количеством воды V в первом сосуде и W во втором. Начальным состоянием является V=0, \V=0, а конечным V=0, W=4. Переходы между состояниями можно записать в виде правил:
сосуды(V1, W1):- сосуды(V2, W2).
Например, правило
сосуды(0, W) :- сосуды(V, W).
означает, что вся вода из первого сосуда вылита. Обратим внимание на слово «вода» в условии задачи. Для предметной области, связанной с водой, характерно то, что воду можно просто выливать, и данное правило перехода между состояниями допустимо. Если бы задача решалась для молока, то его выливать было бы нельзя, и такое правило было бы недопустимым !
Правило
сосуды(3, W) :- сосуды(V, W). означает, что первый сосуд заполнен полностью.
Не разливая, жидкость можно перелить из одного сосуда в другой только так, что один станет пустым, а другой наполнится. Это можно записать в виде правил
сосуды(3,W):- сосуды(V,W-V+3).
сосуды(V,0):- cocyды(V-W,W).
сосуды(V,5): - cocуды(V-W+5,W).
сосуды(0,W):- сосуды(V,W-V).
При решении данной задачи необходимо также избежать повторения одних и тех же состояний - «переливания из пустого в порожнее». Для этого в предикат «сосуды ( )» следует добавить 3-й аргумент - список пройденных состояний П. Элементы в него будут добавляться парами:
сосуды(V1,W1,[V1,W1|П]):- не_принад(V1,W1,П), сосуды(V2,W2,П).
Условие, ограничивающее рекурсию, должно иметь вид:
сосуды(_,4,П) :- write_list(П).
Контрольные вопросы и задания
1. В чем состоят принципиальные различие процедурных и декларативных языков программирования?
2. Каковы этапы программирования на Прологе?
3. Какие типы данных допускает Пролог?
4. В чем существо операции сопоставления?
5. Как реализуются вопросы к программе на Прологе?
6. Приведите примеры рекурсий, отличные от данных в тексте.
7. Для чего служит предикат отсечения?
8. Для чего служат списки и как они задаются?
9. Опишите на Прологе:
а) свою родословную, определите бабушек, дедушек, прабабушек, прадедушек и т.д.;
б) телефонную книгу;
в) районы вашего города, республики, области, укажите численность их на селения, местные достопримечательности;
г) европейские государства ( население, площадь и т.д.);
д) таблицу дат и событий русской истории;
е) небольшой словарь для перевода с русского языка на иностранный язык, который вы изучаете;
ж) ведомость зачета вашей группы;
з) успеваемость вашей группы (дайте определение «отличника»);
и) каталог книг в библиотеке.
10. Запишите на Прологе правила, являющиеся решением следующих заданий:
а) даны два числа а и b, получите их сумму, разность, произведение;
б) дана длина ребра куба, найдите объем куба и площадь его боковой поверхности;
в) дан радиус основания r и высота цилиндра h, найдите его объем и площадь боковой поверхности;
г) даны стороны а и b параллелограмма, а также угол между ними, найдите диагонали параллелограмма и его площадь;
11. Вычислите значения выражений:
а)2х+3у+4
б) (2х+8у+4)/2
в) у-х^2
г) x^2+xy+y^2
д) х/2+5у
е)x^2+3y^2
ж) 5(34х-у)
12. Напишите программы, выполняющие операции над списками:
а) объедините два списка, найдите МАХ и удалите его;
б) удалите из списка элемент, найдите длину оставшегося списка;
в) добавьте к списку элемент, вычислите среднее арифметическое его элементов;
г) обратите список, найдите последний и предпоследний элементы;
д) исключите из списка заданный элемент во всех вхождениях, кроме первого,
найдите длину оставшегося списка;
е) проверьте, имеются ли в списке повторяющиеся элементы, и все их удалите;
ж) удалите из списка все элементы, равные последнему, найдите длину оставшегося списка;
з) объедините два списка, найдите MIN и удалите его;
и) обратите список, найдите МАХ и удалите его;
к) к списку добавьте обращенный второй список, найдите длину результата;
л) отсортируйте список, используя метод пузырька.
13. Напишите программу, решающую задачу о волке, козе и капусте.
14. Напишите программу, решающую задачу, аналогичною задаче 13, о трех туземцах, трех миссионерах и двухместной лодке.
15. Напишите программу, решающею задачу об обходе препятствия.
16. Напишите программу, определяющую положение «шах королю».
17. Напишите программу, определяющую, как шахматному коню попасть с поля
А на поле В.
18. Напишите программу, определяющую, как разлить 10 л молока по 5 л, пользуясь бидонами на 3, 7 и 10 л.
19. Напишите программу, аналитически дифференцирующую элементарную
функцию.
20. Напишите программу, играющую в «крестики и нулики» на бесконечной
плоскости.
21. Напишите программу, вычисляющую интервал между двумя датами одного
года, например 7 марта и 9 сентября.
22. Напишите программу, решающую задачу о четырех ферзях на поле размером
4х4 клетки.
Дата добавления: 2016-02-20; просмотров: 781;
