Понятие алгоритма в информатике. Блок-схемы алгоритмов

Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от латинского написания имени Мухаммеда аль-Хорезми (787 – 850) выдающегося математика средневекового Востока. В своей книге «Об индийском счете» он сформулировал правила записи натуральных чисел с помощью арабских цифр и правила действий над ними столбиком. В дальнейшем алгоритмом стали называть точное предписание, определяющее последовательность действий, обеспечивающую получение требуемого результата из исходных данных. Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством. Создание алгоритма, пусть даже самого простого, – процесс творческий. Он доступен исключительно живым существам, а долгое время считалось, что только человеку. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами.

Данное выше определение алгоритма нельзя считать строгим – не вполне ясно, что такое «точное предписание» или «последовательность действий, обеспечивающая получение требуемого результата». Поэтому обычно формулируют несколько общих свойств алгоритмов, позволяющих отличать алгоритмы от других инструкций.

Такими свойствами являются:

• Дискретность – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.

• Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.

• Конечность – алгоритм должен приводить к решению задачи за конечное число шагов.

• Массовость – алгоритм решения задачи разрабатывается в общем виде, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.

На основании этих свойств алгоритм можно определить как последовательность математических, логических или вместе взятых операций, отличающихся однозначностью, массовостью, направленностью и приводящая к решению всех задач данного класса за конечное число шагов.

Есть разные способы задания алгоритма. Например, последовательность шагов решения можно записать на естественном (разговорном языке). Алгоритм нахождения наибольшего общего делителя (НОД), известный как алгоритм Евклида, состоит в следующем.

1. Большее число делим на меньшее.

2. Если делится без остатка, то меньшее число и есть НОД (конец алгоритма).

3. Если есть остаток, то большее число заменяем на остаток от деления.

4. Переходим к пункту 1.

Такое описание легко позволяет получить результат при расчетах «вручную», с помощью карандаша и бумаги. Однако для автоматизированных, машинных расчетов такой способ представления неудобен, алгоритм должен быть записан на особом, алгоритмическом языке, языке программирования.

Для наглядного представления алгоритма используется язык блок-схем, в котором порядок действий указывается с помощью графических элементов, некоторые из которых показаны в табл.1.

Таблица 1. Основные элементы блок-схемы алгоритмы.

Наименование	Обозначение	Функция
Блок начало-конец		Начало и конец алгоритма. Внутри фигуры записывается соответствующее действие
Блок вычислений		Выполнение одной или нескольких операций, обработка данных любого вида
Проверка условия		Отображает функцию переключательного типа с одним входом и двумя или более альтернативными выходами, из которых только один может быть выбран после вычисления условий, определенных внутри этого элемента.
Предопределенный процесс		Процесс, состоящий из одной или нескольких операций, определенных в другом месте программы (в подпрограмме, модуле).
Ввод/вывод данных		Ввод или вывод данных, имена переменных и вид действия указываются внутри фигуры
Граница цикла		Символ состоит из двух частей − начало и конец цикла − операции, выполняемые внутри цикла, размещаются между ними. Условия цикла и приращения записываются внутри символа начала или конца цикла − в зависимости от типа организации цикла.
Соединитель		Используется для обрыва линии и продолжения ее в другом месте
Комментарий		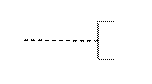Используется для более подробного описания шага, процесса или группы процессов. Описание помещается со стороны квадратной скобки.

Пример блок-схемы алгоритма вычисления факториала целого числа N приведен на рис.1.

Факториал

Ввод N

M : = 1

F : = 1

M : = M + 1 F : = F * M

нет

M = N

да

Вывод F

Конец

Рис.1. Блок-схема алгоритма вычисление факториала числа N

Примечание.Знак «: =»внутри блока вычислений означает операцию присвоения результата, а символ «=» (знак равенства) используется в блоках проверки условия.

Основные правила составления блок-схем:

1) в разветвляющихся процессах любой путь должен приводить к блоку окончания, не должно быть обрывающихся ветвей;

2) из прямоугольника может выходить только одна стрелка;

3) из блока проверки условия должны выходить две стрелки, одна со словом «да», другая – «нет»;

4) если выражение в блоке вычислений громоздкое, вместо него может быть указана ссылка на него, а само выражение приведено в комментарии;

5) если блок-схема велика и не умещается на одной странице, допускается продолжение ее на следующей странице, при этом соединительные линии разрываются с помощью кружочков, внутри которых ставятся одинаковые номера;

6) большие блок-схемы неудобны для использования, поэтому сложные алгоритмы разбивают на фрагменты, модули, которые изображаются на схеме с помощью графического элемента «предопределенный процесс».