Темпы прироста уровней
Если абсолютная скорость прироста уровней динамического ряда характеризуется величиной абсолютных приростов, то относительная скорость прироста уровней – темпами прироста.
Темп прироста представляет собой отношение абсолютного прироста к уровню, принятому за базу. Темпы прироста, как и темпы роста, могут быть выражены в форме коэффициентов и процентов. Коэффициент прироста показывает, на какую долю увеличился или уменьшился последующий уровень по сравнению с предыдущим, т.е.
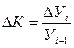 , (9.12)
, (9.12)
где ΔК – коэффициент прироста уровня, выраженный в долях; ΔУi – абсолютный прирост уровня; Уi-1 – предыдущий уровень.
Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился или уменьшился последующий уровень по сравнению с предыдущим, т.е.
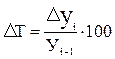 . (9.13)
. (9.13)
Пример. Валовой сбор семян многолетних трав во всех категориях хозяйств административного района составил: в 2009 г. – 45 т, в 2010 г. – 48 т. Необходимо найти темп прироста сбора семян в 2010 г. по сравнению с 2009 г. Для решения прежде всего найдем абсолютный прирост уровней: 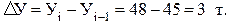 .Затем рассчитаем темп прироста:
.Затем рассчитаем темп прироста:
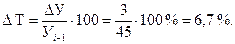
Темпы прироста также, как и темпы роста, могут быть рассчитаны базисным и цепным способами. Между темпами прироста и темпами роста существует непосредственная связь. Поэтому коэффициент (темп) прироста можно выразить через темп роста, т.е.
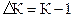 , или
, или 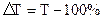 . (9.14)
. (9.14)
Это означает, что коэффициент прироста всегда на единицу меньше соответствующего коэффициента роста. Если же темп прироста выражен в процентах, то он на 100 процентных пунктов меньше темпов роста.
Допустим, если темп роста урожайности зерновых культур составил 118 %, то темп прироста составит:
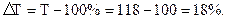
Отсюда следует, что при наличии темпа роста можно удобно и быстро определить темп прироста.
Темпы прироста могут быть выражены положительными (+) и отрицательными (-) значениями. При этом положительные значения темпа указывают на рост последующего уровня по сравнению с предыдущим; отрицательное же значение указывает на его снижение. В последнем случае говорят о темпе снижения.
Результаты исчисления базисных и цепных темпов прироста и снижения покажем на примере динамики реализованных фруктов специализированной сельскохозяйственной организацией (табл. 9.5).
Т а б л и ц а 9.5. Динамика реализации фруктов
| Годы | Реализовано, т | Темпы прироста, % | Темпы прироста (снижения), % | ||
| базисные (к 2007 г) | цепные (к предыдущему году) | базисные (к 2007 г.) | цепные (к предыдущему году) | ||
| 100,0 | 100,0 | 0,0 | 0,0 | ||
| 114,3 | 114,3 | 14,3 | 14,3 | ||
| 100,0 | 87,4 | 0,0 | -12,6 | ||
| 86,8 | 86,8 | 13,2 | -13,2 |
Как видно, темпы роста и темпы прироста в динамике снижаются. Это свидетельствует об убывающем характере динамики реализованной продукции.
Темпы прироста за весь изучаемый период в динамическом ряду могут быть охарактеризованы при помощи их среднего значения. При расчете среднего темпа прироста можно исходить из значения среднего темпа роста, т.е.
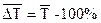 (9.15)
(9.15)
где 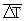 –– средний темп прироста;
–– средний темп прироста; 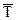 –– средний темп роста.
–– средний темп роста.
Допустим, необходимо определить среднегодовой темп прироста валового сбора картофеля в фермерском хозяйстве за период 2008 – 2010 гг., если в 2008 г. было произведено 120 т, в 2010 – 150 т картофеля.
Прежде всего рассчитаем средний темп валового сбора картофеля по формуле (9.11), т.е.,
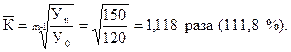
Затем находим средний темп прироста производства картофеля:
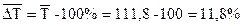
Значит, ежегодный прирост валового сбора картофеля в фермерском хозяйстве за период 2008 – 2010 гг. составил в среднем 11, 8%.
Дата добавления: 2016-02-20; просмотров: 886;
