Водородоподобный атом.
Напомним, что система, состоящая из неподвижного ядра и движущегося вокруг него электрона, называется водородоподобным атомом или водородоподобным ионом.
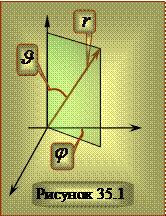Поле, в котором движется электрон, является центрально симметричным. Поэтому при решении уравнения Шрёдингенра в данном случае используют сферическую систему координат: 
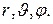Уравнение Шрёдингенра для электрона в центральном поле ядра с зарядом 
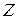имеет вид:
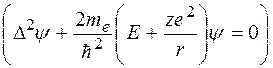(35.1)
Подставив в это уравнение оператор Лапласа в сферических координатах, получим:
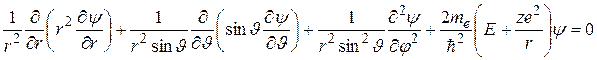(35.2)
Решения (35.2), удовлетворяющие стандартным условиям, получаются при любых положительных Е и при дискретных отрицательных значениях:
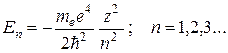(35.3)
Положительные значения энергии соответствуют электрону, пролетающему вблизи ядра и удаляющемуся на бесконечность. Такой электрон не связан с ядром, не образует атом (или ион) и интереса не представляет.
Электрону, связанному с ядром, соответствуют отрицательные значения энергии (35.3). Необходимо подчеркнуть, что эти значения соответствуют значениям, полученным в теории Бора, но в квантовой механике они являются следствием уравнения Шрёдингера, и дополнительных предположений в виде постулатов не требуется.
Собственные функции уравнения Шрёдингера содержат три целочисленных параметра: n, l, m:
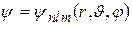
n – называется главным квантовым числом и совпадает с номером уровня энергии в (35.3).
l и m – азимутальное и магнитное квантовые числа, определяющие модуль и проекцию момента импульса на некоторое направление.
Решения, удовлетворяющие стандартным условиям, получаются лишь для значений l, не превышающих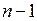 
. Следовательно, при заданном n, азимутальное квантовое число l может иметь значения
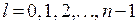(35.4)
При заданном l магнитное квантовое число m может принимать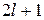 
различных значений:
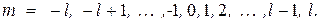(35.5)
Энергия электрона электрона в атоме водорода зависит только от n главного квантового числа (см. (35.3)), поэтому каждому уровню энергии соответствует несколько собственных функций, отличающихся значениями l и m. Таким образом, атом водорода может иметь одну и ту же энергию, находясь в состояниях, описываемых различными волновыми функциями. Энергетические состояния в таком случае называются вырожденными, а число различных состояний, соответствующих данной энергии – кратностью вырождения соответствующего энергетического уровня.
Кратность вырождения энергетических уровней водорода легко рассчитать. Каждому из n значений числа l соответствует 2l + 1 значение m. Таким образом, кратность вырождения можно рассчитать по формуле:
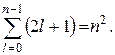
Напомним, что азимутальное квантовое число определяет значение момента импульса, и состояния электрона в атоме водорода с различными значениями азимутального квантового числа l отличаются величиной момента импульса. Электрон, находящийся в состоянии с
l = 0 – называют s-электроном (s состояние);
l = 1 – называют p-электроном (p состояние)
l = 2– называют d-электроном (d состояние)
l = 3 – называют f-электроном (f состояние) и т.д.
При обозначении состояния в котором находится электрон, принято значение главного квантового числа n указывать перед условным обозначением квантового числа l. Поэтому электрон с n = 3 при l = 1 обозначают символами 3p.
Поскольку l < n возможны следующие состояния:
1s
2s 2p
3s 3p 3d
4s 4p 4d 4f и т.д.
Как и в теории Бора, в квантовой механике предполагается, что испускание и поглощение света происходит при переходе электрона с одного уровня на другой. Однако фотон обладает собственным моментом импульса равным приблизительно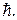 
Поэтому при испускании или поглощении фотона момент импульса атома должен обязательно измениться на 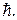Об этом говорят, что при переходах электрона между энергетическими уровнями в атоме должно выполняться правило отбора для азимутального квантового числа:
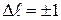(35.6)
Очевидно, что это правило есть просто следствие закона сохранения момента импульса.
Дата добавления: 2016-02-11; просмотров: 1675;