Составление маршрутов движения транспорта
Маршрут движения – это путь следования подвижного состава при выполнении перевозок от начального пункта до конечного.
Маршруты движения классифицируют на маятниковые и кольцевые.
Маятниковым называется такой маршрут, при котором путь следования подвижного состава в прямом и обратном направлениях проходит по одной и той же трассе.
Различают маятниковые маршруты:
- с обратным порожним пробегом, на котором один погрузочный и один разгрузочный пункт;
- с полным использованием пробега, на каждом грузовом пункте которого подвижной состав после разгрузки перемещается на этом же пункте под погрузку другим грузом;
- с неполным использованием пробега, на котором имеется по одному пункту погрузки и разгрузки и один совмещенный пункт, осуществляющий погрузку и разгрузку.
У маятникового маршрута с полным использованием пробега прямым называется направление, по которому следует больший грузопоток, обратным – меньший грузопоток.
Маршрут с обратным порожним пробегом носит название простого маятникового маршрута. Коэффициент использования пробега на нем равен 0,5.
Кольцевым маршрутом называется путь следования подвижного состава по замкнутому контуру, соединяющему несколько пунктов погрузки-разгрузки.
Разновидностью кольцевых маршрутов являются развозочный, сборный и сборно-развозочный.
Развозочным называется маршрут, на котором загруженный подвижной состав развозит груз по нескольким пунктам назначения и постепенно разгружается.
Сборным называется маршрут, на котором подвижной состав последовательно проходит несколько погрузочных пунктов, постепенно загружается и завозит груз в один пункт выгрузки.
Сборно-развозочным называется кольцевой маршрут, на котором одновременно развозится один груз и собирается другой (например, в магазины доставляется молочная продукция и собирается из них тара и поддоны, в которых эта продукция была доставлена накануне).
При составлении маршрутов определяются:
- пути следования автомобиля с грузом и без груза при выполнении сменного задания;
- последовательность объезда пунктов на маршруте;
- конкретизируется время прибытия в каждый из пунктов маршрута;
- при необходимости определяется время отдыха и обеденного перерыва.
Предъявляются жесткие требования не только к срокам, за которые должны быть разработаны маршруты, но и к результатам маршрутизации, так как качество составления маршрутов оказывает определяющее влияние на эффективность доставки
Маятниковым маршрутам с обратным груженым пробегом следует отдавать предпочтение, так как они обеспечивают более высокое значение коэффициента использования пробега, а организовать их проще, чем кольцевые маршруты. Проще осуществляется на маятниковых маршрутах и диспетчерское руководство.
При невозможности организовать маятниковые рациональные маршруты производится планирование кольцевых рациональных маршрутов.
При их организации важно выбрать начальный и конечный пункты маршрутов таким образом, чтобы обеспечить минимальные нулевые пробеги.
Для составления рациональных маршрутов рекомендуется применять математические методы оптимизации и электронно-вычислительную технику.
Составление маршрутов движения транспорта требует согласования пространственно-временных и экономических аспектов. В процессе принятия решений необходимо учитывать:
- характеристики транспортной системы: размещение объектов; производственный и распределительный потенциал; размер спроса; пропускную способность дорог и узлов (соответствующих источникам пополнения, транзитным пунктам и пунктам потребления);
- количественную, стоимостную и качественную характеристику перевозимых грузов;
- спецификацию располагаемых транспортных средств;
- имеющиеся ограничения;
- цели проектирования транспортной сети.
К типичным ограничениям принимаемого решения относятся следующие: ограниченные денежные средства; ограниченное время; ограниченная вместимость; ограниченная мощность; ограничения, накладываемые физико-химическими свойствами перемещаемых грузов.
К типичным целям составления маршрутов в транспортной сети можно отнести следующие: минимизация издержек; максимизация эффективности; максимизация прибыли; минимизация времени (эта цель влияет на минимизацию издержек), минимизация расстояния (эта цель влияет на минимизацию издержек).
Перемещение грузов, по крайней мере между двумя объектами, можно представить в виде сетевой модели. Сеть можно представить с помощью графа или в виде матрицы. На рисунке 5.1. представлен граф и соответствующие ему понятия, благодаря которым можно интерпретировать данную форму представления потока. Граф содержит дуги, которые могут быть как со стрелками, так и без стрелок. Граф, представленный на рисунке 5.1, является направленным, так как стрелки показывают направление потока грузов. Число дуг (представляющих потенциальные или фактические трассы) как выходящих из узла, так и входящих в узел характеризует уровень узла. Узел номер 1 на рисунке 5.1 является узлом 2 уровня, а узел номер 3 – узлом 3 уровня. Также можно утверждать, что граф на рисунке 5.1 не является полным, так как не все его вершины соединены между собой – отсутствует связь между узлами 3 и 5; 1 и 4; 4 и 2; 1 и 2.
| Стрелки называются дугами графа или отрезками |
| Пункты называются узлами или вершинами графа |
| Граф – это система пунктов на плоскости и стрелок, соединяющих некоторые из этих пунктов |
Под трассой понимается линия, по которой можно добраться от одной вершины к другой. Она может состоять из ряда следующих друг за другом дуг. Трасса, на которой ни один узел не встречается более одного раза, называется дорогой,а трасса, по которой можно вернуться к стартовому узлу, называется циклом.Граф также можно представить в виде матрицы. В таблице 5.1 представлена матрица, соответствующая графу, изображенному на рисунке 5.1.
Таблица 5.1. Матричная форма представления материального потока между отдельными поставщиками и потребителями
| Потребители | ||||
| X3 | X5 | Предложение | ||
| Поставщики | X1 | |||
| X4 | ||||
| X2 | ||||
| Спрос |
| А |
| F |
| E |
| B |
| C |
| D |
Далее если дугам или узлам графа придать определенные характеристики (например, пропускная способность, издержки и т.д.) в соответствующих единицах измерения, то получим модель сети (рис. 5.2).
Рис. 5.2. Графическая модель сети
Система распределения обычно включает несколько исходных пунктов и пунктов потребления. Иногда также встречаются транзитные пункты, которые влияют на форму и содержание проходящих через них грузопотоков, хотя преобразование грузов осуществляется в них не всегда. Исходный пункт - это пункт, в котором производятся (добываются) ресурсы и / или с которого начинается грузопоток. Пункт потребления – это место назначения грузопотока или пункт, в котором осуществляется потребление ресурсов. Основная проблема формирования системы распределения заключается в определении объема грузов, которые необходимо переместить из исходного пункта в пункт потребления, чтобы получить максимальную окупаемость и использование ресурсов с учетом существующих условий и ограничений.
Соединение всех пунктов потребления с исходными пунктами при помощи абстрактных звеньев отображает все связи сети. Такая абстрактная сеть описывает возможные пути перемещения грузов из исходных пунктов в пункты потребления.
Пример 5.1
В транспортной сети, модель которой представлена на рисунке 5.3, из узлов А и В, представляющих исходные пункты, необходимо доставить грузы в пункты H, I, F, представляющие пункты потребления с минимальными издержками. В таблице 5.2. представлены издержки на единицу груза на отдельных отрезках сети.
Таблица 5.2. Издержки на единицу груза сij
| Пункты потребления Исходные пункты | A | B | C | D | E | F | G | H | I |
| A | - | - | - | - | - | - | |||
| B | - | - | - | - | - | - | - | ||
| C | - | - | - | - | - | - | |||
| D | - | - | - | - | - | - | |||
| E | - | - | - | - | - | - | - | - | |
| F | - | - | - | - | - | - | - | ||
| G | - | - | - | - | - | - | - | ||
| H | - | - | - | - | - | - | - | - | |
| I | - | - | - | - | - | - | - | - | - |
| A |
| G |
| D |
| B |
| C |
| H |
| I |
| F |
| E |
Рис. 5.3. Модель транспортной сети
Анализ проблемы.
Необходимо принять следующие ограничения:
a) размер спроса должен быть меньше размера предложения, или:
A(+)+B(+) > F(-/+) + I(-) + H(-/+)
б) в сети существует 5 типов узлов:
- узел A является только источником и не может обеспечиваться из какого-либо другого узла. Для него будет верным следующее ограничение:
wAC + wAD + wab ≤ 400,
где wAC – объем груза, перемещаемого из пункта A в пункт С.
- узел I является только пунктом потребления. Для него будет верным следующее ограничение:
wFI + wGI + wHI = 690
- узел B является одновременно источником и транзитным пунктом,
wBD + wBE - wAB ≤ 670
- узлы F и H являются одновременно пунктами потребления и транзитными пунктами,
wEF + wDF -wFG -wFI = 130 для F
wCH + wGH –wHI = 140 для H
- узлы C, D, E, G являются транзитными узлами,
wAC – wCD – wCH – wCG = 0 для C
wAD + wBD + wCD – wDE – wDG – wDF = 0 для D
wBE + wDE – wEF = 0 для E
wCG + wDG + wFG – wGH – wGI = 0 для G
в) объем перемещаемого груза на каждом отрезке транспортной сети должен быть больше или равен нулю:
wij ≥0
г) целевая функция, выбирающая среди допустимых решений такое, которое характеризуется минимальными издержками, может быть записана следующим образом:
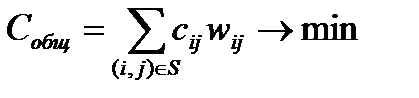
где
S – совокупность отрезков транспортной сети;
Собщ – общие издержки;
сij – издержки, связанные с доставкой единицы груза, относящиеся к данному отрезку;
wij – объем грузов, перевозимых на данном отрезке транспортной сети.
Решение
Необходимо подготовить описание проблемы в соответствии с ограничениями, указанными в пунктах а, б, в, г. Исходная таблица в Microsoft Excel будет выглядеть в виде, представленном на рисунке 5.4.
В ячейку D2 вписываем формулу = G2+G3+G4
В ячейку D3 вписываем формулу = G5+G6-G2
В ячейку D4 вписываем формулу = G3-G7-G8- G9
В ячейку D5 вписываем формулу = G4+G5-G7- G12- G10-G11
В ячейку D6 вписываем формулу = G6+G10-G13
В ячейку D7 вписываем формулу = G11+G13- G14-G15- G17
В ячейку D8 вписываем формулу = G8+G12+G14- G16-G17
В ячейку D9 вписываем формулу = G9+G16-G18
В ячейку D10 вписываем формулу = G15+G17+G18
В ячейки H2-H18 вписывем формулу = FX*GX
В ячейку H19 вписывем формулу = СУММ (H1:H18)
В ячейку H20 вписывем формулу = D2+D3
Ячейки G2-G18 будут заполнены с помощью инстумента «Поиск решения»
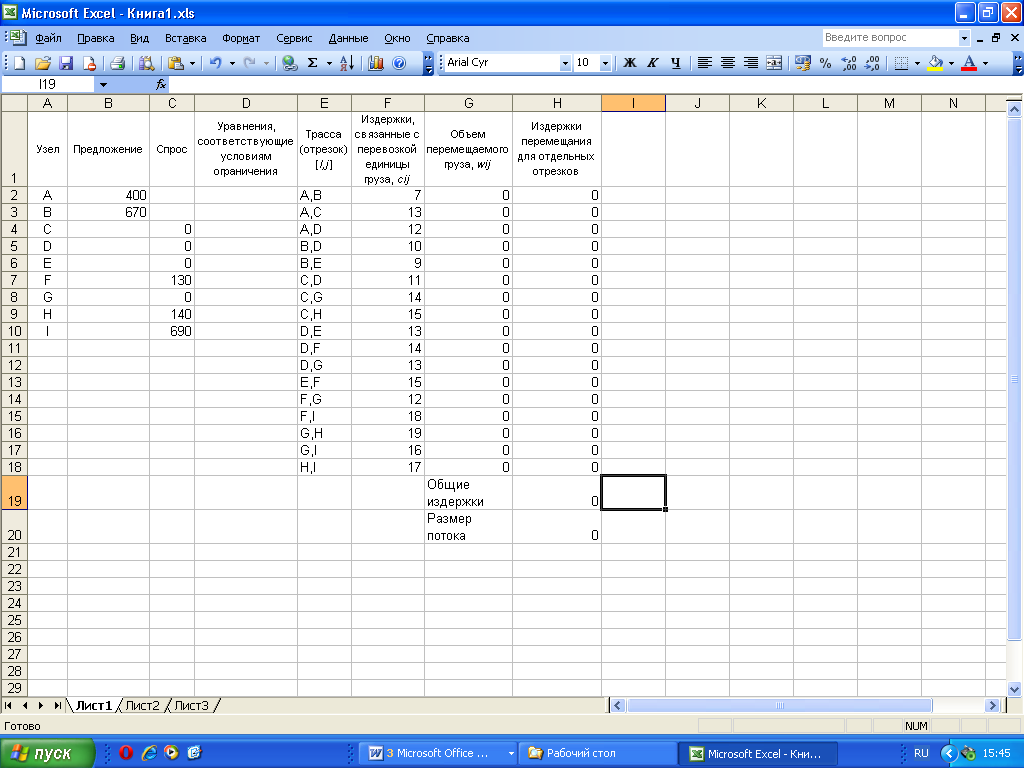
Рис. 5.4. Исходная таблица для решения задачи, изложенной в примере 5.1
Далее используем инструмент «Поиск решения» (рис. 5.5):
- Определение целевой ячейки, значение которой должно быть минимизировано.
- Определение совокупности ячеек, значение которых будет меняться до нахождения минимума целевой ячейки. В данном случае – это объем перевозимых грузов.
- Равенство $D$9= $C$9 является условием для узла H.
- Равенство $D$10= $C$10 является условием для узла I.
- Неравенство $D$2≤$B$2 является условием для узла A.
- Неравенство $D$3≤$B$3 является условием для узла B.
- Равенство $D$4:$D$6=$С$4:$С$6 является условием для узлов C, D, E.
- Неравенство $D$7≤$C$7 является условием для узла F.
- Неравенство $D$8≤$C$8 является условием для узла G.
- Условия, указанные в пунктах 3-9 добавляются с помощью опции «Добавить».
- Затем необходимо установить параметры поиска решения, открыв соответствующую панель.
- На панели «Параметры поиска решения» указываем – «Линейная модель»
- На панели «Параметры поиска решения» также указываем – «Неотрицательные значения».
- Нажимаем клавишу «Выполнить» и получаем решение задачи, изложенной в примере 1 (рис. 5.6).
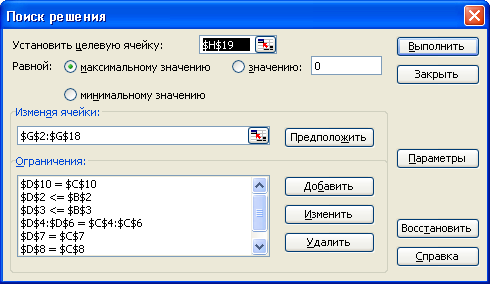
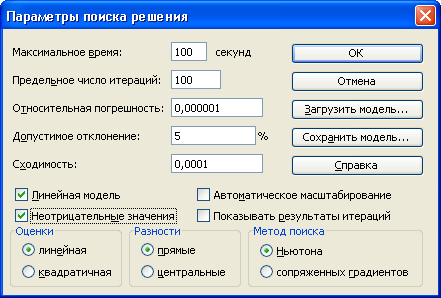
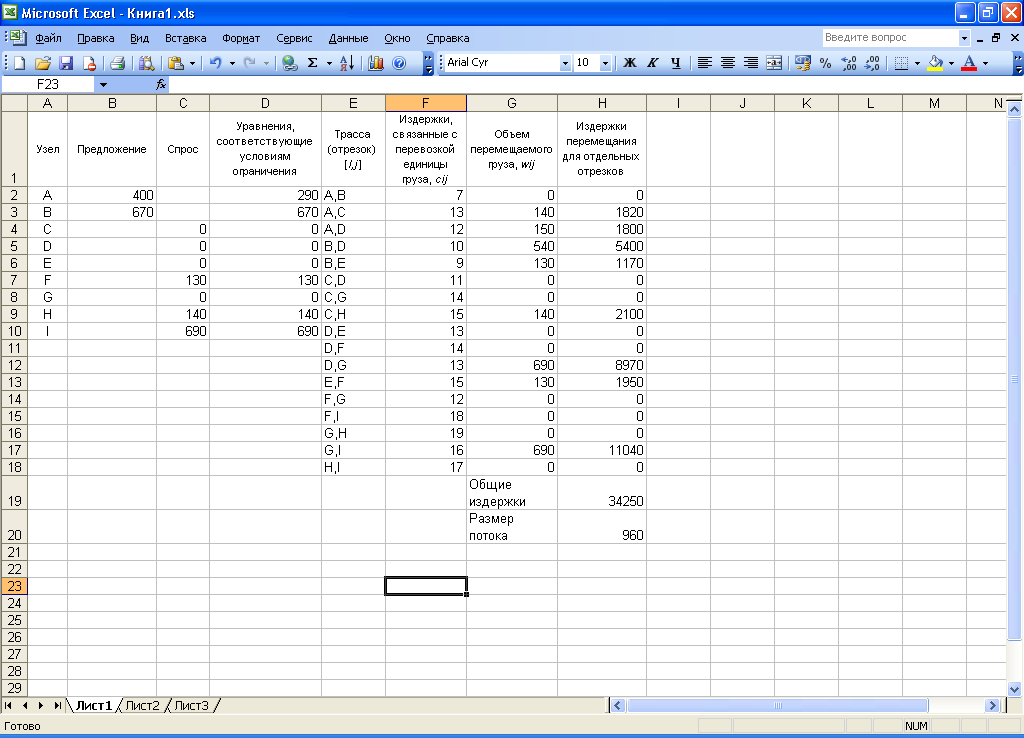
Рис. 5.5. Описание проблемы с помощью инструмента «Поиск решения»
Рис. 5.6. Решение задачи, изложенной в примере 5.1
| A |
| G |
| D |
| B |
| C |
| H |
| I |
| F |
| E |
Решение задачи в виде графика представлено на рисунке 5.7.
Рис. 5.7. Графическое представление решения задачи, изложенной в примере 5.1
В транспортной логистике часто приходится решать задачу поиска наиболее короткой дороги в транспортной сети из пункта A в пункт B. Решение данной задачи также может быть найдено с помощью инструмента «Поиск решения».
Пример 5.2
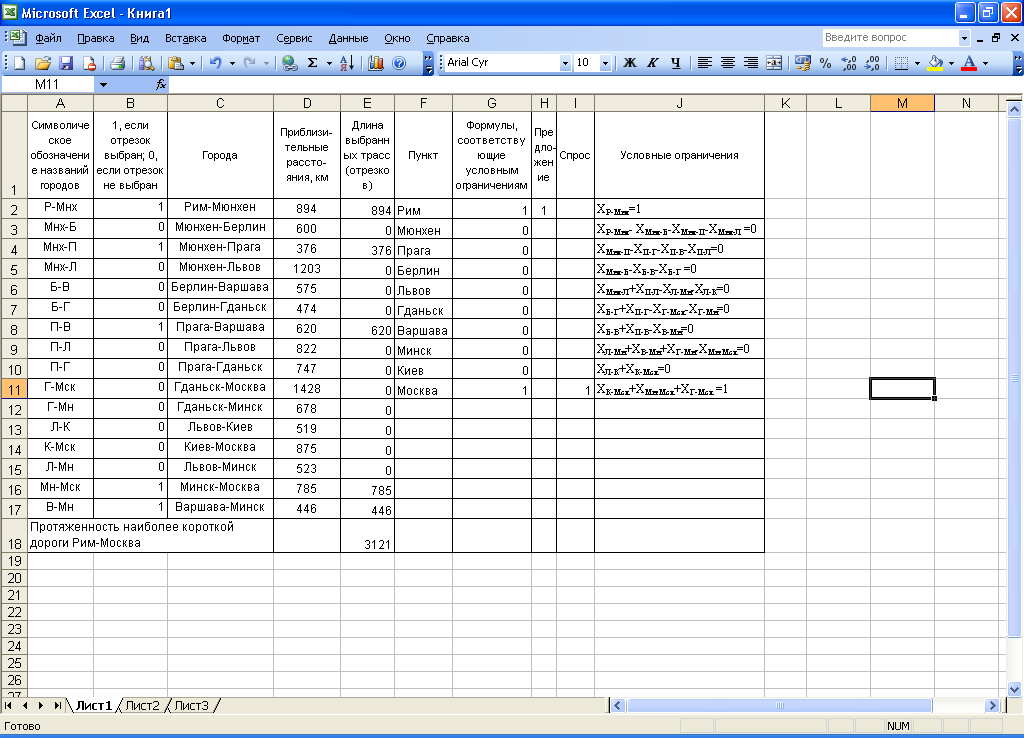
Необходимо довезти груз из Рима в Москву, используя трассы, представленные на рисунке 5.8. Необходимо найти наиболее короткий путь. Приблизительное расстояние между городами приводится ниже.
| Символическое обозначение названий городов | Города | Приблизительные расстояния, км |
| Р-Мнх | Рим-Мюнхен | |
| Мнх-Б | Мюнхен-Берлин | |
| Мнх-П | Мюнхен-Прага | |
| Мнх-Л | Мюнхен-Львов | |
| Б-В | Берлин-Варшава | |
| Б-Г | Берлин-Гданьск | |
| П-В | Прага-Варшава | |
| П-Л | Прага-Львов | |
| П-Г | Прага-Гданьск | |
| Г-Мск | Гданьск-Москва | |
| Г-Мн | Гданьск-Минск | |
| Л-К | Львов-Киев | |
| К-Мск | Киев-Москва | |
| Л-Мн | Львов-Минск | |
| Мн-Мск | Минск-Москва | |
| В-Мн | Варшава-Минск |
| Рим (Р) |
| Мюнхен (Мнх) |
| Берлин (Б) |
| Прага (П) |
| Львов (Л) |
| Варшава (В) |
| Гданьск (Г) |
| Минск (Мн) |
| Киев (К) |
| Москва (Мск) |
Рис. 5.8. Трассы из примера 5.2
Анализ проблемы
Условно принимаем, что Рим является пунктом поставки с потенциалом 1, а Москва – пунктом потребления с потребностью 1, остальные пункты являются транзитными. Необходимо минимизировать издержки по доставке груза из Рима в Москву. Будем считать, что носителем издержек является расстояние, и что издержки пропорциональны расстоянию. Может быть также построена модель, где вместо расстояний будут использоваться данные о времени, требуемом для проезда отдельных отрезков дороги.
Принимаем следующие ограничения:
XР-Мнх=1
XР-Мнх- XМнх-Б-XМнх-П-XМнх-Л =0
XМнх-Б-XБ-В-XБ-Г =0
XМнх-П-XП-Г-XП-В-XП-Л=0
XБ-Г+XП-Г-XГ-Мск-XГ-Мн=0
XБ-В+XП-В-XВ-Мн=0
XМнх-Л+XП-Л-XЛ-Мн-XЛ-К=0
XЛ-Мн+XВ-Мн+XГ-Мн-XМн-Мск=0
XЛ-Мн+XВ-Мн+XГ-Мн-XМн-Мск=0
XЛ-К+XК-Мск=0
XК-Мск+XМн-Мск+XГ-Мск =1
Последовательность решения задачи с использованием инструмента «Поиск решения» представлена на рисунках 5.9-5.11.
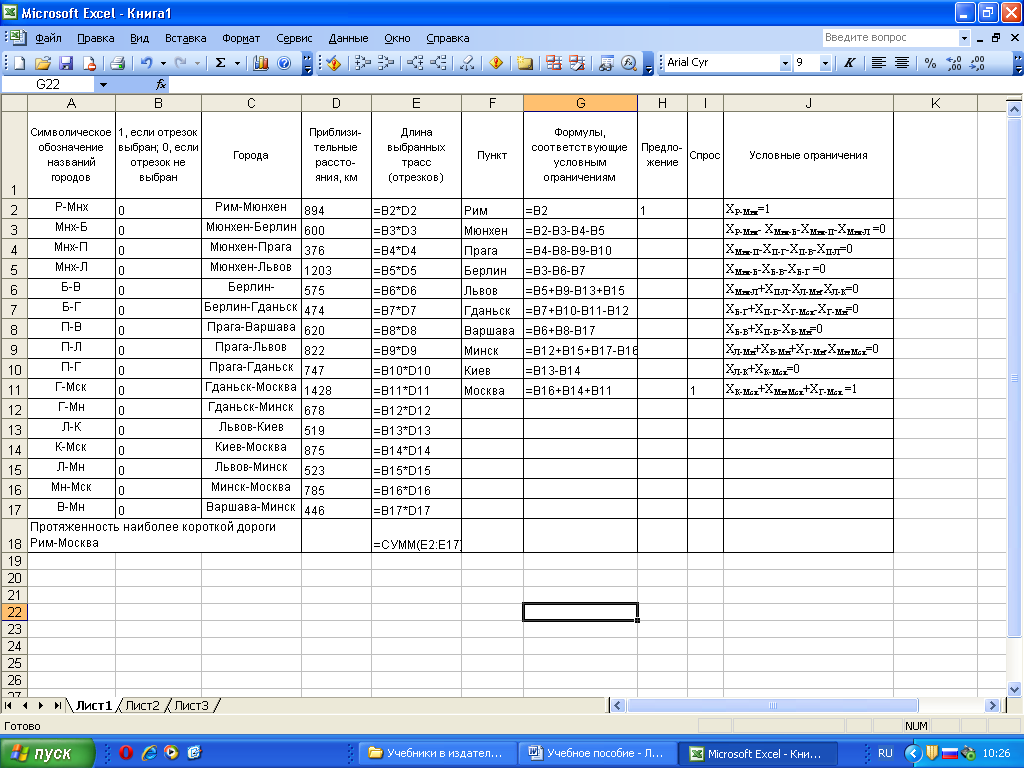
Рис. 5.9. Исходная таблица для решения задачи, изложенной в примере 5.2
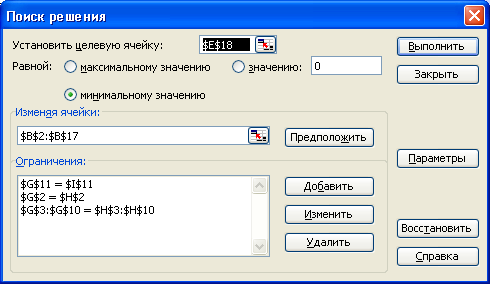
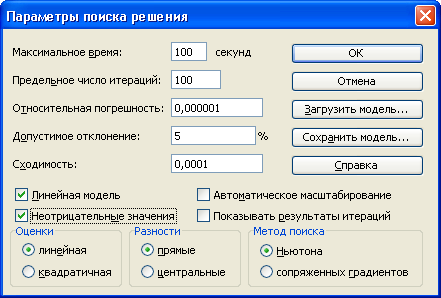
Рис. 5.10. Параметры поиска решения задачи из примера 5.2
Рис. 5.11. Решение задачи из примера 5.2
Дата добавления: 2016-02-20; просмотров: 20040;
