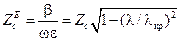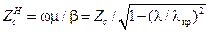Система координат для прямоугольного волновода
Т. к. поперечные составляющие векторов поля выражаются через продольные (см. 13.2), достаточно решить уравнения Гельмгольца относительно последних:
 , ,
| (13.2.8) |
при соответствующих граничных условиях. Как видим, это две скалярные краевые задачи на собственные значения и на собственные функции (собственные волны) поперечного оператора Лапласа. Их решения стандартным методом разделения переменных имеют вид [13.1]:
а) для 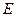 -волн:
-волн:
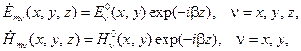
| (13.7.1) |
где для 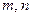 -ой моды (
-ой моды ( 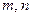 =1, 2, …):
=1, 2, …):
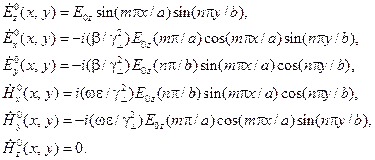
| (13.7.2) |
б) для 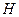 -волн:
-волн:
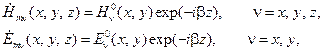
| (13.7.3) |
где для 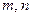 -ой моды (
-ой моды ( 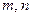 =0, 1, 2, … , кроме одновременного
=0, 1, 2, … , кроме одновременного 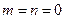 ):
):
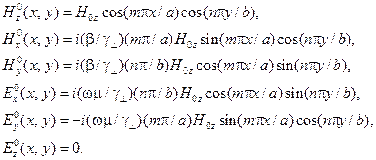
| (13.7.4) |
Как для 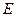 -волны, так и для
-волны, так и для 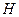 -волны постоянная
-волны постоянная 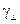 для
для 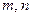 -ой моды находится из соотношения:
-ой моды находится из соотношения:
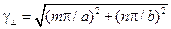 , ,
| (13.7.5) |
а зная ее, из (13.3.5) находится критическая длина волны:
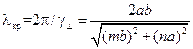 , ,
| (13.7.6) |
длина волны в волноводе:
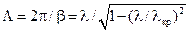 , ,
| (13.3.8) |
и фазовая скорость этой волны:
Характеристическое сопротивление для
|
Заметим, что для 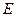 -волны определены все параметры, кроме
-волны определены все параметры, кроме 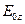 , а для
, а для 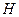 -волны – все параметры, кроме
-волны – все параметры, кроме 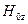 . Для определения этих параметров нужны дополнительные данные, например, мощность источника.
. Для определения этих параметров нужны дополнительные данные, например, мощность источника.
Соотношения (13.7.1), (13.7.2), (13.7.3), (13.7.4) показывают, что в волноводе могут существовать различные моды 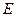 -волн и
-волн и 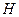 -волн, структура поля и параметры которых зависят от двумерного номера
-волн, структура поля и параметры которых зависят от двумерного номера 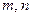 . Эти моды принято обозначать
. Эти моды принято обозначать 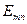 и
и 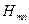 , причем у
, причем у 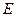 -волн
-волн 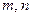 пробегают значения 1, 2, …, а у
пробегают значения 1, 2, …, а у 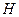 -волн один из индексов (но не оба) может равняться нулю.
-волн один из индексов (но не оба) может равняться нулю.
Чтобы понять смысл номеров 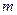 и
и 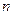 , заметим, что структура поля в поперечном сечении волновода (т. е. при фиксированном значении координаты
, заметим, что структура поля в поперечном сечении волновода (т. е. при фиксированном значении координаты 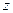 ) аналогична структуре стоячей волны, которую можно характеризовать «длинами волн»
) аналогична структуре стоячей волны, которую можно характеризовать «длинами волн» 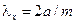 и
и 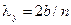 в направлениях осей
в направлениях осей  и
и  соответственно. Таким образом, номер
соответственно. Таким образом, номер 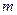 есть число «полуволн» (
есть число «полуволн» (  ), укладывающихся на поперечном размере
), укладывающихся на поперечном размере 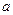 стенки, параллельной оси
стенки, параллельной оси  , а номер
, а номер 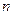 есть число «полуволн» (
есть число «полуволн» ( 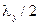 ), укладывающихся на поперечном размере
), укладывающихся на поперечном размере  стенки, параллельной оси
стенки, параллельной оси  . Равенство нулю одного из номеров означает, что поле рассматриваемой волны не зависит от соответствующей координаты (при
. Равенство нулю одного из номеров означает, что поле рассматриваемой волны не зависит от соответствующей координаты (при 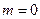 – от координаты
– от координаты 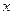 , а при
, а при 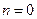 – от координаты
– от координаты 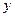 ). Изменение всех составляющих комплексных амплитуд векторов
). Изменение всех составляющих комплексных амплитуд векторов  и
и  вдоль оси
вдоль оси  описывается множителем
описывается множителем  . В волноводе без потерь распространение волны происходит только при
. В волноводе без потерь распространение волны происходит только при 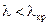 , а критическая длина волны
, а критическая длина волны  зависит, в силу (13.7.6), от размеров
зависит, в силу (13.7.6), от размеров 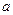 и
и  , от номеров
, от номеров 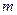 и
и 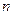 моды. При фиксированных размерах
моды. При фиксированных размерах 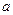 и
и  волновода с увеличением номеров
волновода с увеличением номеров 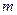 и (или)
и (или) 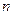 значение
значение  уменьшается.
уменьшается.
Наибольшую  среди всех возможных волн при
среди всех возможных волн при 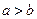 имеет волна
имеет волна 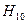 с
с 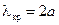 . При
. При 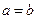 наибольшую
наибольшую  имеют две волны
имеют две волны 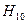 и
и 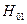 . Волну, имеющую наибольшую
. Волну, имеющую наибольшую  , называют основной волной ЛП (или волной низшего типа). Таким образом, при
, называют основной волной ЛП (или волной низшего типа). Таким образом, при 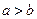 основной волной прямоугольного волновода является волна
основной волной прямоугольного волновода является волна 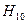 .
.
Волны, у которых 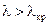 , не распространяются: образуется стоячая волна, в которой
, не распространяются: образуется стоячая волна, в которой 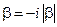 и амплитуды составляющих векторов
и амплитуды составляющих векторов  и
и  экспоненциально убывают вдоль оси
экспоненциально убывают вдоль оси  пропорционально фактору
пропорционально фактору
 , ,
| (13.7.7) |
но это не связано с потерями на поглощение, они по-прежнему предполагаются отсутствующими.
Дата добавления: 2016-02-20; просмотров: 911;

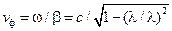 .
.