Виды сечений диэлектрических ЛП

Продолжим классификацию ЛП по конструктивному признаку, перечислив наиболее часто применяемые виды ЛП. Проволочная ЛП – комплекс из двух или четырех проводников, иногда покрытых диэлектриком (рис. 13.1.1). Волноводная ЛП имеет одну замкнутую проводящую поверхность, имеющую вид цилиндра (трубы) прямоугольного, круглого или эллиптического сечения. (рис. 13.1.2). Полосковые ЛП – симметричная, несимметричная, щелевая, копланарная, микрополосковая (рис. 13.1.3). Последняя отличается тем, что ее диэлектрическая подложка имеет большую относительную диэлектрическую проницаемость 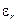(более 10) и малые потери, вследствие чего геометрические размеры устройств, выполненных на основе таких линий, уменьшаются в 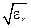раз. Материалом диэлектрической подложки в таких линиях служат поликор, ситалл, кремний, сапфир и др. Если для уменьшения потерь в качестве диэлектрика в полосковой линии используется воздух, то такая линия называется воздушной. Коаксиальная ЛП – двухсвязная линия, жесткая или гибкая, имеющая два проводника прямоугольного или круглого сечения – внутренний и внешний, разделенных диэлектриком или воздухом (в последнем случае линия называется воздушной) (рис. 13.1.4). Диэлектрические ЛП подразделяются по форме поперечного сечения(рис. 13.1.5). Зеркальные диэлектрические ЛП имеют металлический экран.

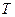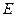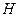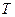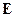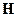Волны, распространяющиеся посредством ЛП, называются направляемыми, в отличие от свободных волн. По своей структуре направляемые волны делятся на поперечные, или -волны (от английского transverse – поперечный); электрические, или -волны; магнитные, или -волны; гибридные. В -волнах векторы и не имеют продольных составляющих, т. е. 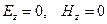. В -в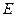олнах вектор 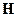не имеет продольной составляющей, т. е. 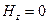, а вектор 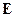имеет как поперечные, так и продольную составляющие. В 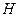-волнах вектор 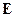не имеет продольной составляющей, т. е. 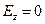, а вектор 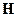имеет как поперечные, так и продольную составляющие. В гибридных, или смешанных волнах и вектор 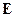, и вектор 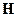наряду с поперечными составляющими имеют и продольные составляющие.

Направляющая система

Рассмотрим произвольную бесконечно протяженную однородную направляющую систему, ориентированную вдоль оси 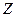. Будем считать, что она состоит из однородных изотропных материалов, не вносит потерь, в ней возбуждены только монохроматические волны одной частоты и сторонние источники отсутствуют. В этих условиях уравнения Максвелла для комплексных амплитуд векторов 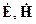имеют вид:

,

(13.2.1)

они сводятся к векторным однородным уравнениям Гельмгольца

(13.2.2)

Для произвольной 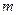-ой моды волн, бегущих вдоль ЛП, зависимость комплексных амплитуд 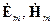от 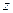имеет вид:

,

(13.2.3)

где 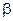=const – коэффициент фазы, 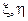-координаты в поперечном сечении ЛП, знак «минус» в показателе экспоненты соответствует, бегущей в положительном направлении оси 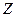, знак «плюс» – бегущей в обратном направлении; пока для определенности рассматриваем волну, бегущую в положительном направлении. С учетом этих выражений, уравнения Гельмгольца примут вид

,

(13.2.4)

где

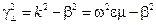
(13.2.5)

– квадрат поперечного волнового числа,

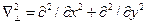
(13.2.6)

– дифференциальный оператор Лапласа в поперечном сечении.

Если вектор 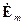и (или) вектор 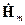имеют продольные составляющие (т. е. если волна в ЛП электрическая, магнитная или гибридная), то нет необходимости решать уравнения Гельмгольца для всех шести составляющих этих векторов 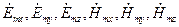, т. к. в этом случае существуют соотношения между поперечными и продольными составляющими этих векторов:

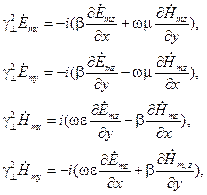
(13.2.7)

и остается только решить скалярные уравнения для продольных составляющих:

,

(13.2.8)

с учетом краевых условий, соответствующих рассматриваемой направляющей системе, а затем найти поперечные составляющие из приведенных равенств.

Электрические и магнитные волны

При решении краевой задачи (13.2.8) одновременно определяется поперечное волновое число 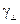, отличное от нуля, если волна электрическая, магнитная или гибридная. Постоянная 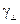зависит от формы и размеров поперечного сечения ЛП и от типа распространяющейся волны, но не зависит от частоты. Из (13.2.5) следует, что

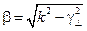
(13.3.1)

и

.

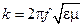(13.3.2)

В зависимости от частоты 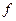подкоренное выражение в (13.3.1) может быть положительным (при 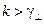), равным нулю (при 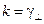) или отрицательным (при 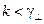). В первом случае параметр 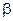– действительное число, фазы составляющих векторов поля в фиксированный момент времени линейно зависят от координаты 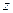, волна распространяется вдоль оси 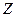с постоянной фазовой скоростью 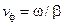и переносит энергию.

В третьем случае 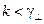параметр 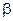чисто мнимый: 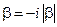, множитель в (13.2.3):

,

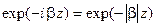(13.3.3)

амплитуды составляющих векторов поля экспоненциально убывают вдоль оси 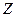, а фазы этих векторов не зависят от координат, т. е. поле имеет характер стоячей волны, экспоненциально убывает вдоль ЛП (что в данном случае не означает потерь энергии), переноса энергии не происходит.

Во втором случае параметр 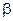=0, частота, соответствующая условию 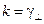, равная

,

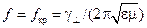(13.3.4)

и отвечающая ей длина волны

,

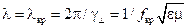(13.3.5)

называются критическими. Выясним смысл этого термина: выражая 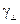из (13.3.5) и подставляя в (13.3.1), получаем:

,

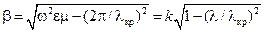(13.3.6)

т. е. коэффициент фазы 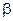действителен, а поле представляет собой распространяющуюся волну, переносящую энергию, только при условии

,

(13.3.7)

называемом условием распространения волны в ЛП; в противном случае энергия не переносится, а поле в форме стоячей волны быстро затухает вдоль 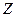. Отметим, что значение 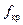(также как соответствующее ему значение 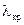) зависит от формы и размеров поперечного сечения ЛП и типа волны (моды).

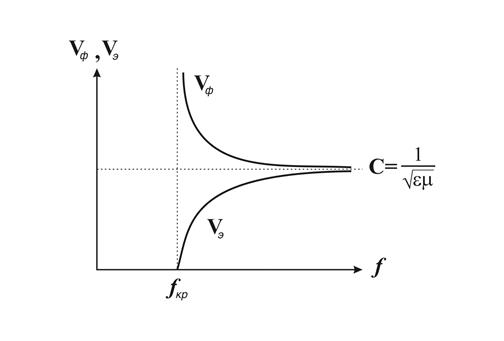
Поскольку длина волны и фазовая скорость в направляющей системе отличаются от соответствующих величин в вакууме, необходимо получить выражения для них. Длиной направляемой волны 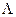называют расстояние между двумя поперечными сечениями ЛП, в которых в один момент времени фазы составляющих вектора 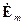отличаются на 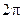, или, то же самое, расстояние, на которое поверхность равной фазы перемещается за период. С учетом экспоненциальной зависимости (13.2.3) всех составляющих векторов 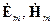поля, это определение приводит к соотношениям:

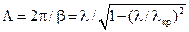
	(13.3.8)
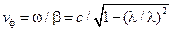
	(13.3.9)

Поскольку длина волны и фазовая скорость свободно распространяющейся волны в безграничной однородной среде без потерь с параметрами 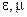равны

,

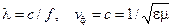(13.3.10)

то сравнение с (13.3.8), (13.3.9) показывает, что эти величины в ЛП больше в 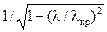раз (см. рис. 13.3.1), причем этот множитель неограниченно возрастает при приближении 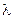к 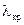слева. Само по себе явление зависимости фазовой скорости волны от частоты называется дисперсией и служит причиной различия фазовой и групповой скоростей, а также искажения формы немонохроматического сигнала при распространении в среде.