Потенциальная яма. Туннельный эффект.
Рассмотрим одномерную бесконечно глубокую потенциальную яму. Потенциал определяется как  для
для 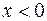 ,
,  для
для  ,
, 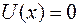 для
для  .
.
Уравнение Шредингера
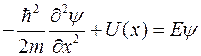 ,
,
Решение с учетом граничных условий
 ,
,  .
.
Энергия стационарного состояния равна
 .
. 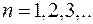
Видим, что энергетический спектр дискретный. Т.о. энергия квантуется. Энергия уровней растет квадратично с ростом 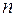 . Число
. Число 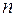 определяет состояние частицы в потенциальной яме. Его называют квантовым числом. Это число не может равняться нулю, ибо это соответствует отсутствию частицы.
определяет состояние частицы в потенциальной яме. Его называют квантовым числом. Это число не может равняться нулю, ибо это соответствует отсутствию частицы.
Туннельный эффект.
Рассмотрим прохождение через потенциальный барьер конечной высоты. Потенциальная энергия в уравнении Шредингера имеет вид
1) 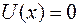 для
для 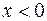 ,
,
2)  для
для  ,
,
3) 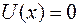 для
для  .
.
В общем виде уравнение Шредингера для всех областей запишется

Его решение 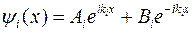
Где для области 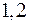 :
:  ,
,
для области  :
: 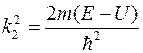 .
.
Рассмотрим случай  . Тогда
. Тогда  и
и  .
.
Волновая функция имеет вид
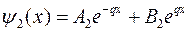 ,
,
Поскольку волновая функция ограничена, то  . Тогда
. Тогда

Рассматривается движение частицы слева направо через барьер. Поскольку квадраты волновой функции определяют плотности вероятности обнаружения частицы в соответствующей области, можно ввести коэффициент прозрачности  .
.
В силу непрерывности волновых функций сшиваем их на границах барьера и получим следующее выражение для коэффициента прозрачности
 .
.
Постоянную  можно положить равной единице. Для потенциальной ямы произвольной формы
можно положить равной единице. Для потенциальной ямы произвольной формы 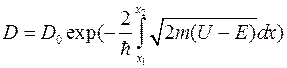 .
.
Таким образом, получили, что частица может оказаться по другую сторону потенциального барьера, высота которого превышает энергию частицы. Вероятность встретить частицу по другую сторону барьера определяется коэффициентом прозрачности. Это явление называется туннельным эффектом. Подобная ситуация никогда не может встретиться в классической физике и в макромире. Туннельный эффект активно используется при создании устройств. На его основе был объяснен 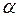 - распад ядер.
- распад ядер.
Дата добавления: 2016-02-20; просмотров: 1141;
