Уравнение баланса мощностей и уравнения напряжения в простейшей электрической цепи.

рис 2.1

Задача: произвести анализ, т.е связать между собой ток, напряжение с параметрами цепи, для этого основополагающим является закон сохранения энергии. Закон сохранения энергии для электрической цепи может быть записан в виде баланса мощностей уравнении равновесия напряжения.

Возможны два события электрической цепи:

-1-режим вынужденных колебаний, когда подключен внешний источник

-2-режим свободных колебаний, когда u(t) отсутствует колебания, возникают за счет энергии накопления в реактивных элементах.

Рассмотрим первый режим - режим свободных колебаний.

Ток цепи, возникающий при свободных колебаниях в ней при u(t)=0 должен подключаться закону сохранения энергии, из которого следует, что убыль запаса электромагнитной энергии в цепи за единицу времени равна тепловой энергии, выделяющейся в сопротивлении за то же время.

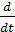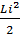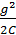- ( + ) = ri²

(2.1)

- уравнение баланса мощностей простейшей схемы в режиме свободных колебаний. Произведем дифференцирование и сокращения, придем к следующему уравнению

- L 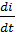+ + 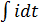ri=0

(2.2 а)

Уравнение равновесия напряжении в режиме свободных колебаний.

u_L+u_C+ u_R=0

т.к при выводе уравнения (2.2) предполагалось, что энергия сосредоточена в отдельных её элементах , где

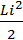- запас энергии в магнитном поле, связанном с катушкой индуктивности;

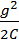- запас энергии в электрическом поле, связанном с конденсатором;

ri^{2 –} количество тепловой энергии

то уравнение (2.2) характерно для последовательной цепи с сосредоточенными параметрами .

При наличии приложенного к цепи внешнего напряжения уравнение баланса мощностей будет:

ri^{2 -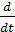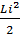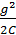} ( + )= ui (2.3)

u i – мощность, поступающая от внешнего источника.

Упростим (2.3) получим

L 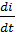+ + 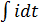ri = u(t) (2.4) - уравнение равновесия напряжения.

Режим вынужденных колебаний:

u_L+u_C+ u_R= u(t) (2.5)

L 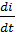+ + 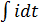ri = u(t)

(2.4) - уравнения равновесия напряжений

Баланс мощностей :

- u - 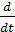( 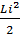+ 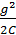) = R i²

Пример: аналогично решается задача о распределение тока в цепи из параллельно соединенных r, L,С

Свободные колебания – когда 1и 1’ разомкнуты , такую цепь удобно анализировать, подключая источник тока.

Уравнения равновесия токов

-режим свободных колебаний

* i_L+i_C+ i_R=0 (2.6)

-режим вынужденных колебаний

* i_L+i_C+ i_R=i(t) (2.7)

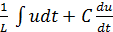+ gu=i(t) (2.8)

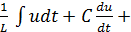gu=0 (2.8a)

(2.8) и (2.2) - баланс мощностей

Для расчета электрических цепей существует также операторный метод.

Замечание:

В сх. 2.1, чтобы был режим свободных колебании , необходимо короткое замыкание зажимов 1-1’.

В сх. 2.2 для свободных колебании нужно осуществить режим холостого хода.

i_с+i_L+ i_r=0 (2.9) - уравнение равновесия токов, где

i_с - ток в ветви с конденсатором;

i_{L - ток в ветви с индуктивностью,}

_т.к u = L 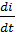→ i_L

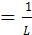
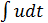
i_r ток в ветви с резистором

i_r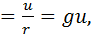

где g - активная проводимость.

Запишем в раскрытом виде:

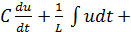gu=0 (2.10)

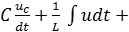gu = i(t) (2.11)