История, предмет, структура информатики 2 страница
3. Формализация – получение знаний о целом или его частях с помощью языков искусственного происхождения (формальное описание, представление).
4. Аксиоматизация – получение знаний о целом или его частях с помощью некоторых аксиом (не доказываемых в данной теории утверждений) и правил получения из них (и из ранее полученных утверждений) новых верных утверждений.
5. Виртуализация – получение знаний о целом или его частях с помощью искусственной среды, ситуации.
Пример. Для построения модели планирования и управления производством в рамках страны, региона или крупной отрасли нужно решить следующие проблемы:
1. определить структурные связи, уровни управления и принятия решений, ресурсы; при этом чаще используются методы наблюдения, сравнения, измерения, эксперимента, анализа и синтеза, дедукции и индукции, эвристический, исторический и логический методы, макетирование и др.;
2. определить гипотезы, цели, возможные проблемы планирования; наиболее используемые методы – наблюдение, сравнение, эксперимент, абстрагирование, анализ, синтез, дедукция, индукция, эвристический, исторический, логический и др.;
3. конструирование эмпирических моделей; наиболее используемые методы – абстрагирование, анализ, синтез, индукция, дедукция, формализация, идеализация и др.;
4. поиск решения проблемы планирования и просчет различных вариантов, директив планирования, поиск оптимального решения; используемые чаще методы – измерение, сравнение, эксперимент, анализ, синтез, индукция, дедукция, актуализация, макетирование, визуализация, виртуализация и др.
Суть задачи управления системой – отделение ценной информации от "шумов" (бесполезного, иногда даже вредного для системы возмущения информации) и выделение информации, которая позволяет этой системе существовать и развиваться.
Информационная система – это система, в которой элементы, структура, цель, ресурсы рассматриваются на информационном уровне (хотя, естественно, имеются и другие уровни рассмотрения).
Информационная среда – это среда (система и ее окружение) из взаимодействующих информационных систем, включая и информацию, актуализируемую в этих системах.
Установление отношений и связей, описание их формальными средствами, языками, разработка соответствующих описаниям моделей, методов, алгоритмов, создание и актуализация технологий, поддерживающих эти модели и методы, и составляет основную задачу информатики как науки, образовательной области, сферы человеческой деятельности.
Информатику можно определить как науку, изучающую неизменные сущности (инварианты) информационных процессов, которые протекают в различных предметных областях, в обществе, в познании, в природе.
3 Лекция: Кодирование и шифрование информации
Рассматриваются основные понятия кодирования и шифрования информации, защиты информации и антивирусной защиты.

В современном обществе успех любого вида деятельности сильно зависит от обладания определенными сведениями (информацией) и от отсутствия их (ее) у конкурентов. Чем сильней проявляется указанный эффект, тем больше потенциальные убытки от злоупотреблений в информационной сфере и тем больше потребность в защите информации. Одним словом, возникновение индустрии обработки информации привело к возникновению индустрии средств ее защиты и к актуализации самой проблемы защиты информации, проблемы информационной безопасности.
Одна из наиболее важных задач (всего общества) – задача кодирования сообщений и шифрования информации.
Вопросами защиты и скрытия информации занимается наука кpиптология (криптос – тайный, логос – наука). Кpиптология имеет два основных напpавления – кpиптогpафию и кpиптоанализ. Цели этих направлений пpотивоположны. Кpиптогpафия занимается построением и исследованием математических методов пpеобpазования инфоpмации, а кpиптоанализ – исследованием возможности pасшифpовки инфоpмации без ключа. Термин "криптография" происходит от двух греческих слов: криптоc и грофейн – писать. Таким образом, это тайнопись, система перекодировки сообщения с целью сделать его непонятным для непосвященных лиц и дисциплина, изучающая общие свойства и принципы систем тайнописи.
Введем некоторые основные понятия кодирования и шифрования.
Код – правило соответствия набора знаков одного множества Х знакам другого множества Y. Если каждому символу Х при кодировании соответствует отдельный знак Y, то это кодирование. Если для каждого символа из Y однозначно отыщется по некоторому правилу его прообраз в X, то это правило называется декодированием.
Кодирование – процесс преобразования букв (слов) алфавита Х в буквы (слова) алфавита Y.
При представлении сообщений в ЭВМ все символы кодируются байтами.
Пример. Если каждый цвет кодировать двумя битами, то можно закодировать не более 22 = 4 цветов, тремя – 23 = 8 цветов, восемью битами (байтом) – 256 цветов.
Сообщение, которое мы хотим передать адресату, назовем открытым сообщением. Оно, естественно, определено над некоторым алфавитом.
Зашифрованное сообщение может быть построено над другим алфавитом. Назовем его закрытым сообщением. Процесс преобразования открытого сообщения в закрытое сообщение и есть шифрование.
Если А – открытое сообщение, В – закрытое сообщение (шифр), f – правило шифрования, то f(A) = B.
Правила шифрования должны быть выбраны так, чтобы зашифрованное сообщение можно было расшифровать. Однотипные правила (например, все шифры типа шифра Цезаря, по которому каждый символ алфавита кодируется отстоящим от него на k позиций символом) объединяются в классы, и внутри класса определяется некоторый параметр (числовой, символьный табличный и т.д.), позволяющий перебирать (варьировать) все правила. Такой параметр называется шифровальным ключом. Он, как правило, секретный и сообщается лишь тому, кто должен прочесть зашифрованное сообщение (обладателю ключа).
При кодировании нет такого секретного ключа, так как кодирование ставит целью лишь более сжатое, компактное представление сообщения.
Если k – ключ, то можно записать f(k(A)) = B. Для каждого ключа k, преобразование f(k) должно быть обратимым, то есть f(k(B)) = A. Совокупность преобразования f(k) и соответствия множества k называется шифром.
Имеются две большие группы шифров: шифры перестановки и шифры замены.
Шифр перестановки изменяет только порядок следования символов исходного сообщения. Это такие шифры, преобразования которых приводят к изменению только следования символов открытого, исходного сообщения.
Шифр замены заменяет каждый символ кодируемого сообщения на другой(ие) символ(ы), не изменяя порядок их следования. Это такие шифры, преобразования которых приводят к замене каждого символа открытого сообщения на другие символы, причем порядок следования символов закрытого сообщения совпадает с порядком следования соответствующих символов открытого сообщения.
Под надежностью понимается способность противостоять взлому шифра. При дешифровке сообщения может быть известно все, кроме ключа, то есть надежность шифра определяется секретностью ключа, а также числом его ключей. Применяется даже открытая криптография, которая использует различные ключи для шифрования, а сам ключ может быть общедоступным, опубликованным. Число ключей при этом может достигать сотни триллионов.
Пример. Один из лучших примеров алгоритма шифрования – принятый в 1977 году Национальным бюро стандартов США алгоритм стандарта шифрования данных DES (Data Encrypted Standard). Исследования алгоритма специалистами показали, что пока нет уязвимых мест, на основе которых можно было бы предложить метод криптоанализа, существенно лучший, чем полный перебор ключей. В июле 1991 года введен в действие аналогичный отечественный криптоалгоритм (стандарта ГОСТ 28147-89), который превосходит DES по надежности.
Криптогpафическая система – семейство Х преобразований открытых текстов. Члены этого семейства индексируются, обозначаются символом k; параметр k является ключом. Множество ключей K – это набор возможных значений ключа k. Обычно ключ представляет собой последовательный ряд букв алфавита.
Открытый текст обычно имеет произвольную длину. Если текст большой и не может быть обработан шифратором (компьютером) целиком, то он разбивается на блоки фиксированной длины, а каждый блок шифруется отдельно, независимо от его положения во входной последовательности. Такие криптосистемы называются системами блочного шифрования.
Криптосистемы разделяются на симметричные с открытым ключом и системы электронной подписи.
В симметричных криптосистемах, как для шифрования, так и для дешифрования, используется один и тот же ключ.
В системах с открытым ключом используются два ключа – открытый и закрытый, которые математически (алгоритмически) связаны друг с другом. Информация шифруется с помощью открытого ключа, который доступен всем желающим, а расшифровывается лишь с помощью закрытого ключа, который известен только получателю сообщения.
Электронной (цифровой) подписью (ЭЦП) называется присоединяемое к тексту его криптографическое преобразование, которое позволяет при получении текста другим пользователем проверить авторство и подлинность сообщения. К ЭЦП предъявляются два основных требования: легкость проверки подлинности подписи; высокая сложность подделки подписи.
Криптография изучает, кроме криптосистем (симметричных, с открытым ключом, электронной подписи), еще и системы управления ключами.
Системы управления ключами – это информационные системы, целью которых является составление и распределение ключей между пользователями информационной системы.
Разработка ключевой, парольной информации является типовой задачей администратора безопасности системы. Ключ может быть сгенерирован как массив нужного размера статистически независимых и равновероятно распределенных на двоичном множестве {0, 1} элементов.
Пример. Для таких целей можно использовать программу, которая вырабатывает ключ по принципу "электронной рулетки". Когда число пользователей, то есть объем необходимой ключевой информации, очень большой, используют чаще аппаратные датчики случайных (псевдослучайных) чисел. Пароли также необходимо менять. Например, известный вирус Морриса пытается войти в систему, последовательно пробуя пароли из своего внутреннего эвристически составленного списка в несколько сотен процедур, имитирующих "сочинение" паролей человеком.
Пароли должен генерировать и раздавать пользователям системный администратор по безопасности, исходя из основного принципа: обеспечения равной вероятности появления каждого из символов алфавита в пароле.
В процессе шифрования, чтобы ключ был использован полностью, необходимо многократно выполнять процедуру кодировки с различными элементами. Базовые циклы заключаются в многократном применении разных элементов ключа и отличаются друг от друга только числом повторения и порядком использования ключевых элементов.
Пример. В банковских системах первоначальный обмен ключами между клиентом и банком осуществляется на магнитных носителях без передачи ключей через открытые компьютерные сети. Секретный ключ клиента хранится на сервере сертификации банка и закрыт для доступа. Для осуществления всех операций с ЭЦП на компьютер клиента устанавливается программное обеспечение, которое предоставляет банк, а все необходимые данные для клиента – открытый, закрытый ключ, логин, пароль и др. — обычно хранятся на отдельной дискете или на специальном устройстве, подключаемом к компьютеру клиента.
Все современные криптосистемы построены по принципу Кирхгоффа: секретность зашифрованных сообщений определяется секретностью ключа.
Это означает, что если даже алгоритм шифрования будет известен криптоаналитику, тот, тем не менее, не в состоянии будет расшифровать закрытое сообщение, если не располагает соответствующим ключом. Все классические шифры соответствуют этому принципу и спроектированы таким образом, чтобы не было пути вскрыть их более эффективным способом, чем полный перебор по всему ключевому пространству, то есть перебор всех возможных значений ключа. Ясно, что стойкость таких шифров определяется размером используемого в них ключа.
Пример. В российских шифрах часто используется 256-битовый ключ, а объем ключевого пространства составляет 2256. Ни на одном реально существующем или возможном в недалеком будущем компьютере нельзя подобрать ключ (полным перебором) за время, меньшее многих сотен лет. Российский криптоалгоритм проектировался с большим запасом надежности, стойкости.
Информационная безопасность информационной системы – защищенность информации, обрабатываемой компьютерной системой, от внутренних (внутрисистемных) или внешних угроз, то есть состояние защищенности информационных ресурсов системы, обеспечивающее устойчивое функционирование, целостность и эволюцию системы. К защищаемой информации (информационным ресурсам системы) относятся электронные документы и спецификации, программное обеспечение, структуры и базы данных и др.
Оценка безопасности компьютерных систем базируется на различных классах защиты систем:
- класс систем минимальной защищенности (класс D);
- класс систем с защитой по усмотрению пользователя (класс C);
- класс систем с обязательной защитой (класс B);
- класс систем с гарантированной защитой (класс A).
Эти классы имеют и подклассы, но мы их не будем здесь детализировать.
Основными типами средств воздействия на компьютерные сети и системы являются компьютерные вирусы, логические бомбы и мины (закладки, жучки), внедрение в информационный обмен.
Пример. Многократно разославшая свой код в 2000 году вирусная программа в Интернете могла при открытии приложения к тексту письма с интригующим заголовком (ILoveYou – ЯТебяЛюблю) рассылать свой код по всем адресам, зафиксированным в адресной книге данного получателя вируса, что приводило к веерному размножению вируса по Интернету, ибо адресная книга каждого пользователя может содержать десятки и сотни адресов.
Компьютерный вирус – специальная программа, которая составлена кем-то со злым умыслом или для демонстрации честолюбивых, в плохом смысле, интересов, способная к воспроизводству своего кода и к переходу от программы к программе (инфицирование). Вирус подобен инфекции, проникающей в кровяные тельца и путешествующей по всему организму человека. Перехватывая управление (прерывания), вирус подключается к работающей программе или к другим программам и затем дает команду компьютеру для записи зараженной версии программы, а затем возвращает управление программе, как ни в чем не бывало. Далее или сразу же этот вирус может заработать (перехватив управление от программы).
По мере появления новых компьютерных вирусов разработчики антивирусных программ пишут вакцину против нее – так называемую антивирусную программу, которая, анализируя файлы, может распознать в них скрытый код вируса и либо удалить этот код (вылечить), либо удалить зараженный файл. Базы антивирусных программ обновляются часто.
Пример. Известная антивирусная программа AVP лаборатории Касперского содержит в своей базе данные о нескольких десятках тысяч вирусах, вылечиваемых программой, и обновляется ежедневно.
Вирусы бывают следующих основных видов:
- загрузочные – заражающие стартовые секторы дисков, где находится самая важная информация о структуре и файлах диска (служебные области диска, так называемые boot-сектора);
- аппаратно-вредные – приводящие к нарушению работы, а то и вовсе к разрушению аппаратуры, например, к резонансному воздействию на винчестер, к "пробою" точки на экране дисплея;
- программные – заражающие исполняемые файлы (например, exe-файлы с непосредственно запускаемыми программами);
- полиморфные – которые претерпевают изменения (мутации) от заражения к заражению, от носителя к носителю;
- стелс-вирусы – маскирующиеся, незаметные (не определяющие себя ни размером, ни прямым действием);
- макровирусы – заражающие документы и шаблоны текстовых редакторов, используемые при их создании;
- многоцелевые вирусы.
Особенно опасны вирусы в компьютерных сетях, так как они могут парализовать работу всей сети.
Вирусы могут проникать в сеть, например:
- с внешних носителей информации (из копируемых файлов, с дискет);
- через электронную почту (из присоединенных к письму файлов);
- через Интернет (из загружаемых файлов).
Существуют различные методы и пакеты программ для борьбы с вирусами (антивирусные пакеты).
При выборе антивирусных средств необходимо придерживаться следующих простых принципов (аналогичных противогриппозной профилактике):
- если используются в системе различные платформы, операционные среды, то антивирусный пакет должен поддерживать все эти платформы;
- антивирусный пакет должен быть простым и понятным, дружественным в использовании, позволяющим выбирать опции однозначно и определенно на каждом шаге работы, иметь развитую систему понятных и информативных подсказок;
- антивирусный пакет должен обнаруживать – скажем, с помощью различных эвристических процедур – новые неизвестные вирусы и иметь пополняемую и обновляемую регулярно базу данных о вирусах;
- антивирусный пакет должен быть лицензионным, от надежного известного поставщика и производителя, который регулярно обновляет базу данных, а сам поставщик должен иметь свой антивирусный центр – сервер, откуда можно получить необходимую срочную помощь, информацию.
Пример. Исследования свидетельствуют, что, если половина компьютеров в мире будет иметь постоянную, эффективную антивирусную защиту, то компьютерные вирусы лишатся возможности размножаться.
4 Лекция: Системы счисления и действия в них:
Рассматриваются основные понятия числовых систем, правила их построения, выполнение действий в них.

Алфавит Х из р символов и правила записи (изображения) и обработки чисел с помощью символов этого алфавита называются системой счисления (нумерацией) с основанием р. Число х в системе с основанием р обозначается как (х)р или хр.
Любая система счисления – это система кодирования числовых величин (количеств), позволяющая выполнять операции кодирования и декодирования, то есть по любой количественной величине однозначно находить его кодовое представление и по любой кодовой записи – восстанавливать соответствующую ей числовую величину.
Все системы счисления строятся по общему принципу: определяется величина р – основание системы, а любое число х записывается в виде комбинации степеней веса р от 0-й до n-й степени следующим образом:
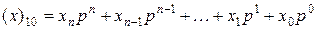 .
.
Наиболее используемые в информатике системы счисления, кроме, естественно, десятичной, – это:
1) двоичная, над алфавитом Х = {0,1};
2) восьмеричная, над Х = {0,1,2,3,4,5,6,7};
3) шестнадцатеричная, над Х = {0,1,2,3,4,5,6,7,8,9,А,В,С,D,Е,F}, где символы А, В, С, D, Е, F имеют, соответственно, десятичные веса 10, 11, 12, 13, 14, 15.
Пример. 11012 = 1 × 23 + 1 × 22 + 0 × 21 + 1 × 20 = 8 + 4 + 1 = 1310 ,
1578 = 1 × 82 + 5 × 81 + 7 × 80 = 64 + 40 + 7 = 11110 ,
A6F16 = 10 × 256 + 6 × 16 + 15 × 1 = 267110 .
В большинстве систем счисления вес цифры (или символа алфавита) зависит от ее места в записи числа или слова. Такая система счисления называется позиционной; в противном случае система называется непозиционной.
Пример. Непозиционная система – древняя римская система записи чисел с алфавитом вида Х={I (1), V (5), Х (10), L (50), С (100), D (500), М (1000)}, где в скобках указаны веса символов (не зависящие от позиции символа). Примеры римских чисел (в скобках – обычные десятичные эквиваленты): III (3), IV (4), V (5), VI (6), IX (9), XI (11), DCL (650). Запись числа в этой системе получается двусторонней конкатенацией, причем правая конкатенация ассоциируется с добавлением, а левая конкатенация – с убавлением (например, IV и VI). Поразрядное же выполнение арифметических операций не имеет места (например, XIV + IV ≠XVIII ).
Для изображения десятичных дробей используется подобная формула разложения по степеням основания.
Пример. 110,0012 = 1×22 + 1×21 + 0×20 + 0×2-1 + 0×2-2 + 1×2-3 = 6,12510;
A,B16 = A×160 + B×16-1 = 10×1 + 11×0,0625 = 10,687510 .
Процедура перевода десятичных чисел в р-ную систему счисления:
1. перевести отдельно целую часть числа х, для чего последовательно делить сперва целую часть [х]10 , а затем все частные (получаемые при делении) на р до тех пор, пока не получим в очередном частном число меньшее р; изображение [х]p получается последовательным приписыванием к последнему частному остатков от деления – от последнего до первого;
2. перевести отдельно дробную часть (мантиссу) числа, то есть {x}10 , для чего последовательно умножать сперва исходную мантиссу, а затем мантиссы получаемых чисел на р до тех пор, пока не получим мантиссу, равную нулю, или нужное количество цифр в {х}p; изображение {х}p получается приписыванием к целой части первого произведения второй такой же цифры и т.д., до последней цифры целой части;
3. результат будет иметь вид (х)р = [х]p,{х}p .
Пример. Найти: 12,810 = ?2 . Решение:
1. Переводим целую часть: 1210 =11002;
2. Переводим дробную часть:
0,8×2 = 1,6; 0,6×2 = 1,2; 0,2×2 = 0,4; 0,4×2 = 0,8; 0,810 = 0,11001100...2;
3. результат перевода: 12,810 = 1100,11001100...2 .
Пример. Найдем 29,2510 = ?8 . Решение имеет вид:
1. 2910 = 358;
2. 0,2510 = 0,28;
3. 29,2510 = 35,28.
Пример. Найдем 79,2610 = ?16 . Решение:
1. 7910 = 4F16 ;
2. 0,2610 = 0,4016 ;
3. 79,2610 = 4F,416 .
При переводе дробной части мы ограничились нахождением двух значащих цифр после запятой, ибо перевод точно сделать невозможно.
Для перевода из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной в 16-ную и обратно, используется таблица следующего вида:
| ОСНОВАНИЕ СИСТЕМЫ | |||
| — | |||
| — | |||
| — | |||
| — | |||
| — | |||
| — | |||
| — | — | ||
| — | — | ||
| — | — | ||
| — | — | ||
| — | — | ||
| — | — | ||
| — | — | ||
| — | — |
При переводе в 8-ную систему или из нее необходимо группировать в тройки биты, а при переводе в 16-ную или из нее – группировать их в четверки битов. Можно добавлять, если нужно, незначащие нули (слева от целой части и справа от мантиссы) или отбрасывать их.
Пример. Рассмотрим переводы в смешанных системах.
1. Из 2-ной системы в 8-ную (двоично-восьмеричное изображение):
| 101,101112= | 101, | |||
| 58 | 58 | 68 | =5,568 |
2. Из 8-ной системы в 2-ную (восьмерично-двоичное изображение):
| 6,248= | 6, | |||
| 1102 | 0102 | 1002 | =110,01012 |
3. Из 2-ной системы в 16-ную (двоично-шестнадцатеричное изображение):
| 101,101112= | 0101, | |||
| 516 | 11(B)16 | 816 | =5,B816 |
4. Из 16-ной системы в 2-ную (шестнадцатерично-двоичное изображение):
| 1A,F316= | A, | F | |||
| 00012 | 10102 | 11112 | 00113 | =11010,111100112 |
Арифметические операции в двоичной системе осуществляются согласно нижеприведенной таблице:
| x | y | x+y | x–y | x×y | x/y |
| – | |||||
| 1* | |||||
| – | |||||
*При вычитании из 0 происходит заем единицы их старшего разряда, т.е. 0–1=10–1=1.
Обратным кодом числа в системе с основанием р называется число в этой системе, получаемое заменой цифры(символа) в каждом разряде числа на его дополнение до максимальной цифры в системе (т.е. до р–1).
Дополнительный код получается путем добавления к младшему разряду обратного кода единицы.
Пример.
1. Для двоичного числа 10011 обратный код 01100, дополнительный 01101;
2. Для восьмеричного числа 457 обратный код 320, дополнительный – 321;
3. Для шестнадцатеричного числа А9 обратный код 56, дополнительный – 57.
Использование дополнительного кода позволяет свести операцию вычитания к операции сложения. Алгоритм вычитания с помощью дополнительного кода:
- найти дополнительный код вычитаемого такой же разрядности, как и уменьшаемое,
- сложить этот код с уменьшаемым.
Результатом вычитания будет полученная сумма без учета старшего разряда (отбрасывается).
Пример. Выполним вычитание напрямую и через сложение (через дополнительный код):
1101102 1101102
-101012 + 10112 дополнительный код
1000012 11000012 сумма
отбрасываемая единица
Целые числа в математике и их аналоги в n-разрядных арифметиках тождественны (по количеству) в рамках их представления с этой разрядностью. При этом можно отметить основные отличия представления чисел в поле памяти человека и в поле памяти n-разрядной арифметики:
1. Бесконечное и счетное множество целых чисел представляется отрезком [–N; +N], где N – максимальное число, представимое в этой арифметике (многоточие – общее число единиц, равное n): N = (111…1)2;
2. Бесконечное и несчетное множество действительных чисел 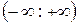 , располагающееся на числовой оси равномерно и плотно, представляется в n-разрядной арифметике множеством с неравномерной плотностью (сгущение у нуля и сжатость со стороны меньших чисел);
, располагающееся на числовой оси равномерно и плотно, представляется в n-разрядной арифметике множеством с неравномерной плотностью (сгущение у нуля и сжатость со стороны меньших чисел);
Дата добавления: 2016-02-09; просмотров: 676;
