Смеси идеальных газов

Для всей смеси в целом основное уравнение кинетической теории газов

,

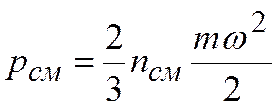где 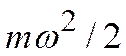– средняя кинетическая энергия молекул для всей смеси в целом, может быть представлено в виде формулы

.

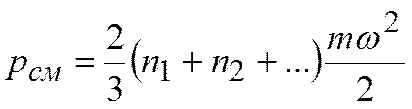Учитывая, что все компоненты находятся при одной и той же температуре, из уравнения Больцмана имеем:

,

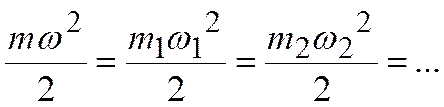откуда следует закон Дальтона:

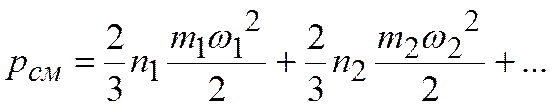
Из закона Бойля – Мариотта:

,

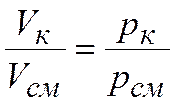где V_к – приведенный объем, который занял бы компонент, находясь отдельно от других компонентов при давлении и температуре смеси.

Последнее выражение можно записать в таком виде

.

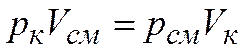Составляя такие выражения для каждого из компонентов, а затем складывая их левые и правые части, получаем

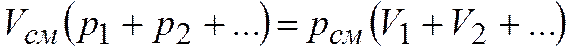
и, производя сокращение на основании закона Дальтона, находим окончательно

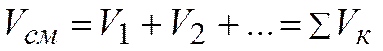
т.е. объем газовой смеси равен сумме приведенных объемов ее компонентов.

Газовая смесь характеризуется своим мольным (Z_к), объемным (r_к) или массовым составом (m_к).

Для пересчета объемного состава в массовый и наоборот введено понятие о средней (кажущейся) молекулярной массе смеси m_см .

Общая масса смеси идеальных газов

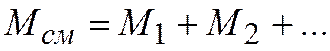
Масса компонента смеси ,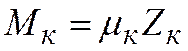

Для однородного газа .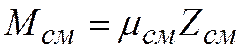

Отсюда ,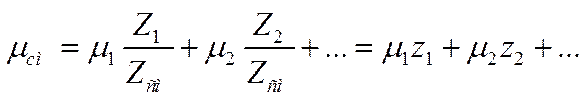

где z₁, z₂ … – мольные доли компонентов смеси.

Также, среднюю молекулярную массу смеси можно выразить через молекулярные массы компонентов и их объемные доли:

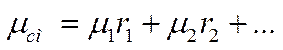
Пересчет объемного состава на массовый и наоборот производится на основе следующих соотношений между объемными и массовыми долями компонентов:

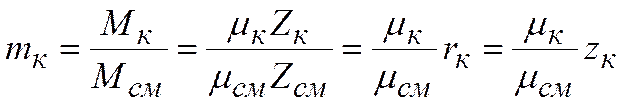
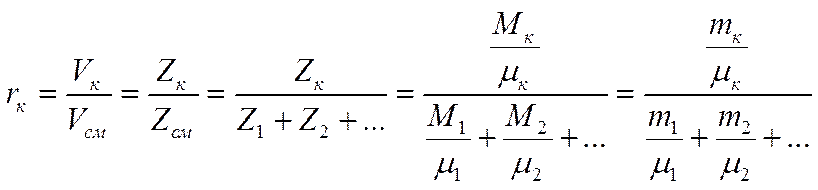
Уравнение состояния для всей смеси в целом имеет вид

,

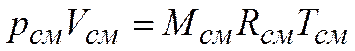а для каждого из компонентов может быть записано так:

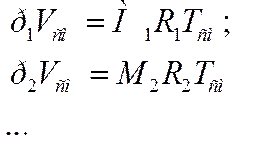
Учитывая, что ,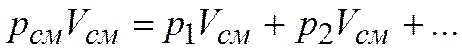

получаем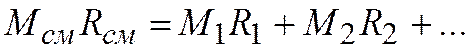

или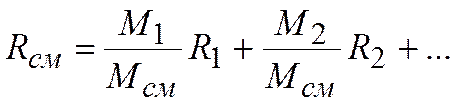

и окончательно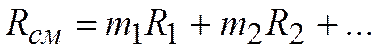

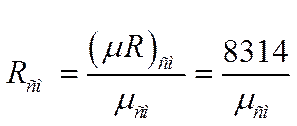, Дж/(кг×град)