Лекция 2. Понятие как форма мысли.

Предмет и значение логики. Основные законы логики.

Термин «логика» происходит от греческого слова «logos», что значит «мысль», «слово», «разум», и используется для обозначения как совокупности правил, которым подчиняется процесс мышления, так и науки о правилах мышления и о тех формах, в которых оно осуществляется. Мышление изучается не только логикой, но и рядом других наук, при этом каждая из них изучает мышление в определенном, присущем ей аспекте. Логика исследует мышление как средство познания объективного мира, исследует прежде всего его формы и законы, изучает мышление в его неразрывной связи с языком. Поскольку процессы познания мира в полном объёме изучаются философией, логика является философской наукой.

Логической формой конкретной мысли является строение этой мысли, способ связи элементов её содержания. Структуру мысли, т.е. её логическую форму можно выразить при помощи символов - логических постоянных и логических переменных. Формализация является одним из важнейших методов логического исследования. Основными формами абстрактного мышления являются понятия, суждения и умозаключения. Знание логики повышает культуру мышления, способствует четкости, последовательности, доказательности рассуждения, усиливает эффективность и убедительность речи.

II

Логика одна из древнейших наук. В Европе она начинает формироваться приблизительно в V-IV веках до н.э. Логические проблемы решали Сократ, Протагор, Демокрит, Платон, первое систематическое изложение логики дал Аристотель. [U1] Он видел в логике прежде всего орудие, или метод исследования. Основным содержанием аристотелевской логики является терия дедукции (силлогистика), она оказала огромное влияние на всё последующее развитие логического знания. Английский философ Фрэнсис Бэкон [U2] разработал основы индуктивной логики, методы определения причинной связи между явлениями. Далее, в XIX веке, разработка вопросов научной индукции была продолжена Дж.Ст.Миллем и другими логиками.

Немецкий философ и математик Г.В.Лейбниц [Д3] по праву считается основоположником математической логики, он первым применил математические методы для исследования форм мысли, пытался создать универсальный язык, с помощью которого споры между людьми можно было бы разрешать посредством вычисления. Лейбниц полагал, что математику можно свести к логике (логицизм), а логику считал априоной наукой. Интенсивное развитие математическая логика получила в работах Д.Буля, Э.Шрёдера, С.Джевонса, Г.Фреге, Б.Рассела. Сегодня невозможно представить себе прогресс логического знания без математических логик. Союз логики и математики оказался удивительно продуктивным как для логики, так и для математики. Одним из результатов этого союза стало появление информатики и вычислительной техники.

III

Закон мышления – это необходимая, существенная, устойчивая связь между мыслями. Наиболее простые и необходимые связи между мыслями выражаются законами тождества, непротиворечия, исключенного третьего, достаточного основания.Эти законы лежат в основе различных логических операций с понятиями и суждениями, используются в ходе умозаключений и доказательств. Законы логики имеют общечеловеческий характер: они едины для всех культур. Эти законы сложились в результате многовековой практики человечества, но они являются законами мышления, а не законами самих вещей и явлений мира. Первые три закона были сформулированы Аристотелем, четвертый закон был сформулирован Лейбницем. Аристотелевы законы логически связаны: каждый последующий вытекает из предыдущего. Четвёртый закон имеет самостоятельное значение. Кроме этих четырёх постулатов существует много других формально-логических законов (каждая формула, каждое правило логики – это логический закон), которым должно подчиняться правильное мышление.

Закон тождества формулируется так: любая мысль должна оставаться тождественной себе в процессе всего рассуждения. Тождественность себе означает неизменность. Математическое выражение закона тождества:а=а. Логическая константа, присутствующая в этой формуле, называется эквиваленцией. В мышлении закон тождества выступает в качестве нормативного правила. Оно означает, что нельзя подменять одно суждение (либо понятие) другим. Нельзя тождественные мысли выдавать за различные, а различные – за тождественные. Нарушения закона тождества делятся на две разновидности: софизм [U4] (умышленное нарушение закона тождества) и паралогизм [U5] (неумышленное нарушение). Вариантами нарушения закона тождества являются такие распространенные логическиие ошибки как подмена понятия и подмена тезиса.

Закон непротиворечия: два противоположных суждения не могут быть истинными в одно и то же время и в одном и том же отношении. Этот закон является запретом на формально-логические противоречия, как на признаки путаного, неправильного рассуждения. Математическое выражение закона непротиворечия: ┐(а & ┐а). Логическая постоянная, присутствующая в этой формуле, называется конъюнкцией. Формально-логическое противоречие возникает тогда, когда пытаются считать истинными суждения, не совместимые между собой, либо одновременно утверждается и отрицается одно и то же суждение. Подобные логические затруднения называются «сведением к абсурду». [U6] Закон непротиворечия не исключает одновременной ложности противоположных (контрарных) суждений.

Закон исключенного третьего формулируется так: из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано. Математическое выражение третьего закона логики: а v ┐а. Логическая константа, присутствующая в этой формуле, называется дизъюнкцией. Противоречащими суждениями (контрадикторными, взаимноотрицающими) являются следующие пары простых суждений:

1. «Данное S есть P» и «Данное S не есть P» (единичные суждения)

2. «Все S есть P» и «Некоторые S не есть P» (суждения А и О)

3. «Ни одно S не есть P» и «Некоторые S есть P» (суждения Е и I)

Закон исключенного третьего предполагает чёткий выбор одной из двух взаимоисключающих альтернатив. Третий закон логики позволяет строить особый тип доказательства – доказательство от противного.

Закон достаточного основания гласит: всякая истинная мысль должна быть достаточно обоснована. Формулы для этого закона нет, так как он имеет содержательный характер: обоснованность либо необоснованность тезиса определяются прежде всего содержанием аргументов. Четвёртый закон логики является требованием доказательности познающего мир мышления. В то же время закон этот является требованием понимания, знания причин исследуемых явлений.

Лекция 2. Понятие как форма мысли.

ПЛАН

1. Общая логическая характеристика понятия. Содержание и объем понятия.Закон обратного отношения содержания и объёма.

2. Виды понятий по объёму и содержанию.

3. Отношения между понятиями. Типы совместимости и типы несовметимости.

Понятие – это форма мысли, в которой фиксируются общие и существенные признаки класса или единичного предмета. Признаки – это то, чем предметы сходны друг с другом, или отличны друг от друга. Признаками являются свойства и отношения. Существенные признаки – это те из них, каждый их которых необходим, а все вместе взятые достаточны, чтобы с их помощью можно было выделить данный класс (предмет) из всех остальных, либо обобщить однородные предметы в класс.

В языке понятия выражаются словами или словосочетаниями. Но понятие и слово не тождественны: понятие – это смысл слова, а слово – имя понятия. Свидетельством этому является множество языков, соотвествующих единому процессу мышления, наличие в одном и том же языке слов-синонимов и слов-омонимов.

Основными логическими приёмами формирования понятий являются анализ, синтез, сравнение, абстрагирование, обобщение.Для выделения существенных признаков необходимо абстрагироваться (отвлечься) от несущественных признаков, которых в любом предмете очень много. Этому помогает сравнение, сопоставление предметов. Для выделения ряда признаков требуется произвести анализ, т.е. мысленно расчленить целый предмет на его составные части, элементы, стороны, отдельные признаки. Обратная операция – синтез (мысленное объединение) частей предмета, отдельных признаков в единое целое. Понятие формируется на основе обобщения существенных признаков, присущих ряду однородных предметов.

Всякое понятие имеет содержание и объём.Содержанием понятия называется совокупность существенных признаков одноэлементного класса или класса однородных предметов, отраженных в этом понятии. Содержание – это качественная, смысловая сторона понятия.Объёмом понятия называется совокупность (класс) предметов (элементов), которая мыслится в понятии. Объём – количественная, измеряемая сторона понятия. Объёмы понятий деляться на конечные (регистрируемые) и бесконечные (нерегистрируемые). Закон обратного отношения содержания понятия и его объёма гласит: чем богаче содержание понятия, тем меньше его объём; чем беднее содержание, тем больше, обширнее объём понятия. В этом законе речь идёт о понятиях, находящихся в родо-видовых отношениях: содержание видового понятия богаче признаками, чем содержание родового понятия. Действие этого закона удобно проиллюстрировать графически. На схемах объёмы понятий символизируются площадями кругов (круги Эйлера).

Понятия классифицируются по объёму и по содержанию. По объему всё множество понятий делится на три класса: единичное понятие, общее понятие и пустое понятие. Единичное понятие содержит в своём объёме один единственный уникальный объект (например: «Эльбрус», «Пушкин»). Общее понятие содержит в объёме некоторое множество элементов («человек», «поэт»). Общие понятия деляться на регистрируемые и нерегистрируемые множества. Среди нерегистрируемых множеств выделяют особую группу понятий - категории (универсалии) – понятия предельной степени общности (например: «число», «материя», «время»). В процессе рассуждения общие понятия могут употребляться в собирательном и разделительном (несобирательном) смыслах. Если понятие относится ко всему классу предметов, взятых в их единстве, и неприложимо к каждому элементу класса в отдельности, то такое употребление понятия называется собирательным (например: библиотека как собрание книг, парламент как сборище депутатов). Если содержание понятия относится к каждому элементу класса в отдельности, то такое его употребление называется несобирательным (например: книга, студент). Пустое понятие – это понятие в объёме которого отсутствуют элементы («вечный двигатель», «кентавр»).

По содержанию понятия делятся дихотомически, т.е. - на пары. Выделяют три пары видов понятий по содержанию.

Конкретные и абстрактные понятия. Понятия, в которых обобщаются конкретные предметы, явления, события по тем или иным признакам, называются конкретными («книга», «растение»). Понятия, в которых мысляться свойства предметов или отношения между ними, называются абстрактными («красота», «смелость», «скорость»).

Положительные и отрицательные понятия. Понятия, в которых отражаются присущие предметам признаки (не обязательно хорошие), называются положительными («грамотный человек», «порядок», «грубиян»). Понятия, в которых признаки, составляющие содержание понятия, отрицаются, называются отрицательными («неграмотный», «беспорядок»). В языке отрицательные понятия выражаются обычно словами с отрицающими частицами, но, если в процессе языковой эволюции отрицающая частица слилась со значимой частью слова, то понятие считается положительным («неурядица», «негодяй»).

Относительные и безотносительные (абсолютные) понятия. Относительные (парные) понятия настолько содержательно связаны друг с другом, что сохраняют смыслы только в парах («левое направление и правое направление», «причина и следствие»). Безотносительными (абсолютными) понятиями называются те из них, которые существуют самостоятельно и не нуждаются в четко фиксированных парах ( «человек», «число»).

Определить к каким видам относится то или иное понятие – значит дать ему логическую характеристику. Логическая характеристика понятия уточняет его смысл, который не всегда раскрывается в именующем его слове.

Далёкие друг от друга по содержанию понятия называются несравнимыми. Считается, что несравнимые понятия не могут соединяться в одном контексте, не могут вступать в логические отношения. Понятия, имеющие нечто общее в содержаниях, называются сравнимыми.Такие понятия вступают в логические отношения. Логические отношения – это отношения между объёмами сравнимых понятий. Эти отношения являются необходимым фундаментом мышления: понятия существуют в мышлении не изолированно, они постоянно соотносятся, образуя более сложные формы – суждения, логические выводы. Логические отношения между понятиями делятся на отношения совместимости и отношенитя несовместимости.

Отношения совместимости – это отношения между понятиями, объёмы которых совпадают полностью или частично. Типы совметимости – это отношение равнозначности, отношение подчинения и отношение пересечения. Отношение равнозначности (тождества) возникает между понятиями, которые имеют различные содержания, но один и тот же объём (например: «равносторонний треугольник – равноугольный треугольник»). Отношение подчинения (субординация) характеризуется тем, что объём одного понятия полностью входит в объём другого, но не исчерпывает его («цветок – роза»). Понятия, объёмы которых совпадают частично, т.е. содержат общие элементы, находятся в отношении пересечения (например: «горожанин – садовод»). Отношения между понятиями изображаются обычно с помощью круговых схем Эйлера.

Отношение равнозначности Отношение подчинения

А, В А

В

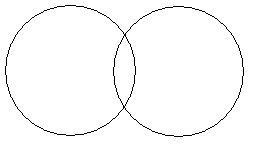
А В

Отношение пересечения

Отношения несовметимости – это отношения между понятиями, объёмы которых не совпадают ни в одном элементе. Типы несовместимости – это отношение соподчинения (координация), отношение противоположности (контрарность) и отношение противоречия (контрадикция).Соподчинение (координация) – это отношение между понятиями, исключающими друг друга, но принадлежащими некоторому более общему понятию. Соподчинение – это отношение между видами рода в тех случаях, когда у видов нет общих элементов («пианино, скрипка, виолончель»). В отношении противоположности (контрарности) находятся объёмы таких двух понятий, которые являются видами одного рода, и притом одно из них содержит какие-то признаки, а другое – заменяет эти признаки исключающими, противоположными признаками («лёд и пламень»). В отношении противоречия (контрадикции) находятся такие два понятия, которые являются видами одного рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, не заменяя их никакими другими. Два контрадикторных вида в совокупности исчерпывают объём рода. Противоречащие друг другу виды обычно бывают положительным и отрицательным понятиями («чётное число, нечётное число»).

Отношение соподчинения Отношение контрарности

А В А В

А не-А

Отношение контрадикции