Гипотезы применяемы при расчете пластин

Основные понятия.

Пластинка – это призматическая или цилиндрическое тело высота (толщина) которого мала по сравнению с размерами в плане.

Срединнаяплоскость – плоскость, которая делит пластину пополам по толщине. При изгибе пластинки, срединная плоскость превращается в изогнутую срединную поверхность пластинки.

Линейныйэлемент – отрезок прямой, соединяющий внешние поверхности пластины перпендикулярно к срединной плоскости. Длина линейного элемента равна толщине пластины.

Контурпластинки – это линия пересечения боковой поверхности пластинки со срединной плоскостью.

В инженерной практике чаще всего встречаются прямоугольные и круглые пластинки (Рисунок.1.)

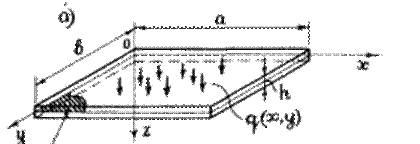
Рис.1. Прямоугольная (а) и круглая (б) пластинки

Условие закрепления пластинки:

· Закрепление по контур;

· Промежуточные опоры;

· Свободные края от закрепления;

Пластины могут быть постоянной и переменной толщины. В зависимости от соотношения между основными размерами пластины и её прогиба различают категории:

Толстые плиты – это пластины, у которых 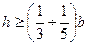, где b – минимальный размер в плане. Толстые плиты применяются в качестве фундаментов зданий, гидротехнических сооружений, опорных частей станков и машин. Расчет производится на основании уравнений пространственной задачи теории упругости;

Тонкие пластины – пластины, у которых 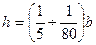где b – наименьший размер в плане. Прогиб составляет не более 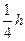. Тонкие пластинки применяются в строительстве в качестве железобетонных плит и панелей жилых и промышленных зданий, металлических настилов, днищ резервуаров;

Гибкие пластины – это пластины, у которых прогибы соизмеримы с толщиной. Гибкие пластины применяются в приборостроение и авиастроение. Расчет производится, учитывая геометрическую нелинейность. Изгиб пластины вызывается действием поперечных нагрузок перпендикулярных к срединной плоскости. Абсолютно гибкая пластина (мембрана) это пластина, у которой прогибы значительно превосходят толщину. Такие пластинки обладают малой жесткостью на изгиб и в основном работают на растяжение в срединной плоскости. При расчете гибких пластин учитывают работу на изгиб на растяжение и сжатие в срединной плоскости.

Жесткая пластина – это пластина, у которой прогибы малы по сравнению с толщиной. 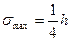. При расчете жестких пластин учитывается только работа на изгиб.

Гипотезы применяемы при расчете пластин

1) Гипотеза прямых нормалей.

Любой линейный элемент при изгибе остается прямым и перпендикулярным к срединной поверхности пластины после деформации. Исходя из этого следует что сдвиги в поперечных плоскостях отсутствуют. 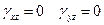.Длина линейного элемента не изменяется следовательно линейная деформация в направлении Z отсутствует: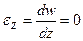

2) Гипотеза о нерастежимости срединной плоскости

В срединной плоскости отсутствует деформация растяжения сжатия и сдвига следовательно срединная плоскость является нейтральной. 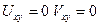. Давление между слоями отсутствует. Сигма=0

3)Гипотеза об отсутствии давления между слоями пластинки

Перемещение и деформации в пластине при изгибе.

Рассмотрим изгиб пластинки под действием поперечной нагрузки. При соотношения Коши с учетом гипотез, получаем:

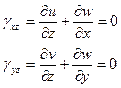
Откуда:

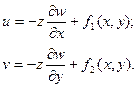
С учетом 2-й гипотезы, получаем:

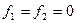
Тогда перемещения равно:

(*)

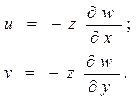Линейное и угловое дифференцирование из формы Коши, равна:

(**)

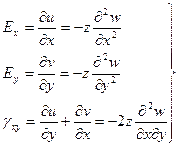Напряжение в пластинах при изгибе

Из формул обобщенного закона Гука с учетом гипотез и формулы (**) получаем:

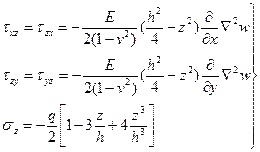
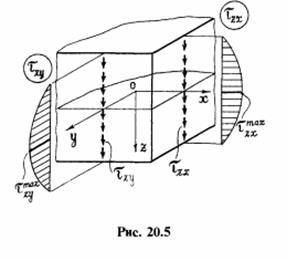
Полученное напряжение изменяется по толщине пластинки по линейному закону(Рисунок 2)

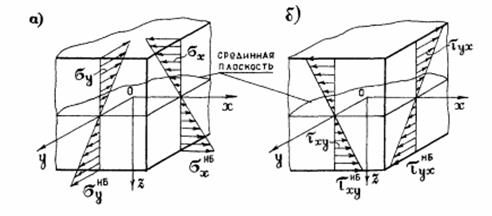
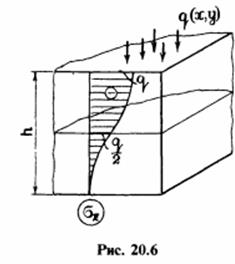
Усилия в пластинках. Дифференциальные уравнения изогнутой срединной поверхности пластинки (Уравнение Софьи Жермен)

Формула(***)Вписать в нее(20.7)(20.9)

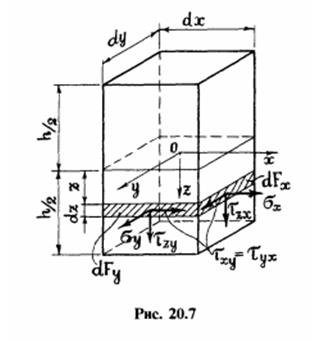
Тогда внутренние силовые факторы (погонные усилия – изгибающие моменты и поперечные силы, крутящий момент) с учетом граничных условий и с учетом (***) в сечениях пластинки перпендикулярных к её срединной плоскости под действием поперечной нагрузки равны:

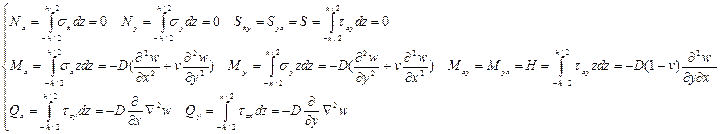
Где D(формула 20.11) цилиндрическая жесткость пластинки.

Граничные условия

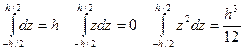
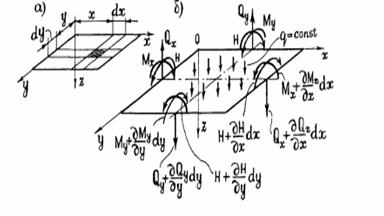
Под действием внешней нагрузки на гранях элемента пластинки возникают внутренние усилия (Рисунок.4.)(20.9)

Из условия равновесия выделенного элемента получаем

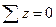
(20.15 первое уравнение)

Сумма моментов относительно X=0 есть (20.15 3 выражение)

Сумма моментов относительно Y=0 есть (20.15 2 выражение)

А)

Б)

С)

Подставим Б и С в А, ис учетом 4тогда получим дифференциальное уравнение изогнутой срединной поверхности пластинки (Уравнение Софьи Жермэн):

(Самуль 8.15 и 8.16 переписать)