Шифрование перестановкой
При этом методе открытый текст разбивается на группы определенной длины. Ключом задается порядок перестановки букв в группе.
При перестановке (транспозиции) буквы исходного открытого текста в сообщении не заменяются другими буквами алфавита, как в классических шифрах, а просто переставляются. Например, слово “THINK” после перестановки может выглядеть как шифрованный текст HKTNI. На рис. 9.5 приведен пример бинарной перестановки данных (линейная операция). Видно, что входные данные просто перемешиваются или переставляются. Преобразование выполняется с помощью блока перестановки (permutation block, P-блок). Технология, используемая сама по себе, имеет один основной недостаток: она уязвима по отношению к обманным сообщениям. Обманное сообщение изображено на рисунке 9.5. Подача на вход единственной 1 (при остальных 0) позволяет обнаружить одну из внутренних связей. Если криптоаналитику необходимо выполнить криптоанализ такой системы с помощью атаки открытого текста , он отправит последовательность таких обманных сообщений, при каждой передаче смещая единственную 1 на одну позицию. Таким образом, обнаруживаются все связи входа и выхода. Данный пример показывает, почему защищенность системы не должна зависеть от ее архитектуры.
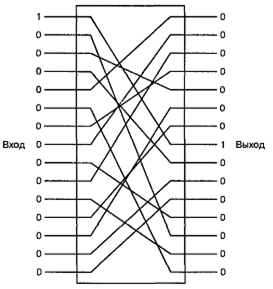
Рисунок 9.5 – Блок перестановки
Пример 9.9.Открытый текст «СДАЧА ЗАЧЕТА ПО ТЕЛЕМЕХАНИКЕ» правила перестановки группы из семи букв с порядковыми номерами
1 – 2 – 3 – 4 – 5 – 6 – 7 переставить в порядок – 7 – 1 – 5 – 3 – 6 – 4 – 2.
Шифртекст (криптограмма) «ЗСАА□ЧДПААЕ□ТЧМОЛТЕЕ□ЕЕИАКНХ».
Можно использовать и усложненную перестановку. Для этого открытый текст записывается в матрицу по определенному ключу К1. Шифртекст образуется при считывании из этой матрицы по ключу К2.
Пример 9.10.Открытый текст «ШИФРОВАНИЕ ПЕРЕСТАНОВКОЙ».
Матрица из четырех столбцов приведена в таблице 9.11, где запись по строкам в соответствии с ключом K1: 5 – 3 – 1 – 2 – 4 – 6, а чтение по столбцам в соответствии с ключом К2: 4–2–3–1
Таблица 9.11 - Матрица алфавита с перестановкой из четырех столбцов
| И | Е | □ | П | |
| Е | Р | Е | с | |
| В | А | Н | ||
| Т | А | Н | о | |
| ш | И | Ф | Р | |
| в | К | О | й | |
| K1/K2 |
Шифртекст «ПСНОРЙЕРВАИК□ЕАНФОИЕОТШВ».
Наиболее сложные перестановки осуществляются по гамильтоновым путям, которых в графе может быть несколько.
Пример 9.11. Открытый текст «ШИФРОВАНИЕ ПЕРЕСТАНОВКОЙ» Ключ – гамильтонов путь на графе (рисунок 9.6).
 |
Рисунок 9.6 – Гамильтонов путь на графе
Шифртекст «ШАОНИРФВИЕЕСЕП□РТОВЙАОНК»
Чтение криптограммы (1 – 7 – 5 – 8 – 2 – 4 – 3 – 6).
Запись открытого текста (1 – 2 – 3 – 4 – 5 – 6 – 7 – 8).
Необходимо отметить, что для данного графа из восьми вершин можно предложить несколько маршрутов записи открытого текста и несколько гамильтоновых путей для чтения криптограмм.
В 1991 г. В.М. Кузьмич предложил схему перестановки, основанную на кубике Рубика. Согласно этой схеме открытый текст записывается в ячейки граней куба по строкам. После осуществления заданного числа заданных поворотов слоев куба считывание шифртекста осуществляется по столбцам. Сложность расшифрования в этом случае определяется числом ячеек на гранях куба и сложностью выполненных поворотов слоев. Перестановка, основанная на кубике Рубика, получила название объемной (многомерной) перестановки [12].
В 1992-1994 гг. идея применения объемной перестановки для шифрования открытого текста получила дальнейшее развитие. Усовершенствованная схема перестановок по принципу кубика Рубика, в которой наряду с открытым текстом перестановке подвергаются и функциональные элементы самого алгоритма шифрования легла в основу секретной системы «Рубикон». В качестве прообразов пространственных многомерных структур, на основании объемных преобразований которых осуществляются перестановки, в системе «Рубикон» используются трехмерный куб и тетраэдр.
Дата добавления: 2016-02-04; просмотров: 1554;
