Качество процесса управления САУ в установившемся режиме

Для большей наглядности мы будем рассматривать структурную схему одноконтурной системы, представленную на рисунке 82.

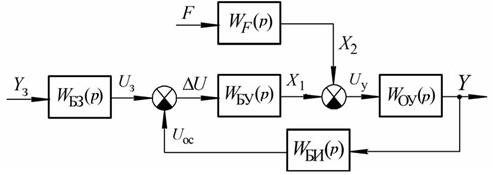
Рис.82. Структурная схема одноконтурной САУ

Упростим структурную схему, преобразовав ее в соответствии с правилами преобразования, к следующему виду:

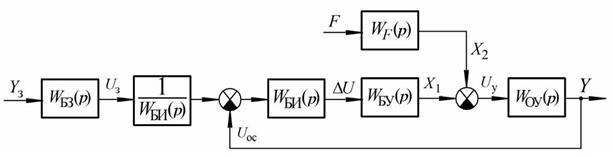
Рис.83. Упрощенная структурная схема одноконтурной САУ

Для того, чтобы согласовать сигналы u_з(t) и u_ос(t), необходимо подобрать одинаковые передаточные функции W_БЗ (р) и W_БИ(р), поэтому должно выполняться равенство

W_БЗ (р) = W_БИ(р). С учетом этого условия структурную схему системы можно будет представить в виде, изображенном на рисунке 84, где ошибку регулирования δ (t), можно выразить в тех же единицах измерения, что и значения задающего параметра y_з(t) и выходного параметра y(t).

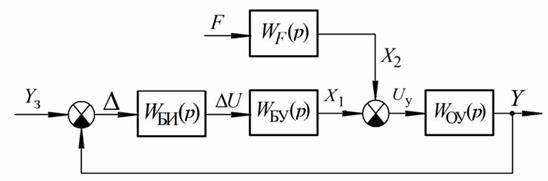
Рис.84. Структурная схема САУ после преобразования

В данном случае изображение ошибки регулирования Δвходит в формулу для определения сигнала рассогласования, который можно выразить, как:

ΔU(р) = Δ(р) W_БИ(р) (2.66.)

Ошибка δ(t) зависит от величины параметров задающего и возмущающего воздействий, поэтому ее значение можно выразить, как сумму ошибок данных воздействий и представить, как:

δ(t) =δ_y(t) + δ_f(t) (2.67.)

Выразим передаточные функции в следующем виде:

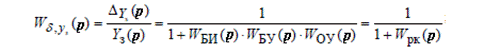(2.68.)

и

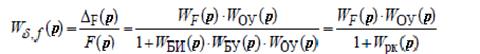(2.69.)

Передаточную функцию разомкнутого контура мы выразили, как:

W_рк (р) =W_БИ(р) W_БУ (р) W_ОУ(р) (2.70.)

Следовательно, исходя из выражений (2.68.) и (2.69.) величину изображения ошибки можно представить следующим образом:

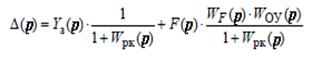(2.71.)

Существуют типовые законы оценки установившегося режима, которыми установлены

следующие условия:

а) задающее и возмущающее воздействия постоянны и не изменяются во времени, т.е.

y_з(t), f (t) = const (2.72.)

б) изменения в системе происходят с постоянной скоростью, т.е.

y_з (t) = a t и f (t) = const (2.73.)

в) изменения в системе происходят с постоянным ускорением, т.е.

y(t) = b t²/2и f (t) = const (2.74.)

г) изменения в системе происходят по гармоническому закону, т.е.

y_з (t) = y₀ sin(ω t) и f (t) = const (2.75.)

Статической ошибкой называется значение ошибки регулирования δ (∞) при постоянной величине входного воздействия.

Статической системой называется система, у которой при постоянной величине входного воздействия, значения ошибок входного и возмущающего воздействий не равны нулю.

Статической по возмущающему воздействию называется система, у которой при постоянной величине входного воздействия, при значении ошибки входного воздействия равной нулю, ошибка возмущающего воздействия не равна нулю.

Астатической называется система, у которой значения ошибок входного и возмущающего воздействий равны нулю.

Астатической по задающему воздействию называется система, у которой значение ошибки входного воздействия не равно нулю, а ошибка возмущающего воздействия равна нулю.

Так как значение передаточной функции разомкнутого контура выражается следующим образом:

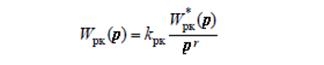(2.76.)

в данном случае 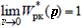, r- количество нулевых корней полинома A(р) или порядок астатизма системы.

Существование системы статической по задающему воздействию и астатической по возмущающему воздействию является невозможным.

Точность статической системы улучшается с увеличением передаточного коэффициента разомкнутого контура k_рк.

Существует также коэффициент статизма системы, который вычисляется по формуле:

s = 1 / 1 + k_рк (2.77.)