Оценка устойчивости системы управления второго порядка

На примере термического агрегата, структурная схема которого изображена на рисунке 58, представим, что звено системы (нагреватель) имеет определенную инерционность Т_ио. Передаточная функция данного звена будет выглядеть, как:

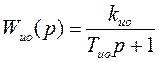(2.55.)

Передаточная функция замкнутой системы будет представлена в виде:

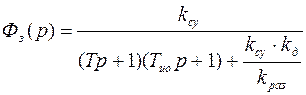(2.56.)

Совершив преобразование, получим следующий вид передаточной функции замкнутой системы:

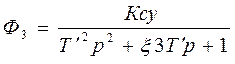(2.57.)

где

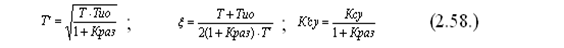
Корни характеристического уравнения будут иметь следующий вид:

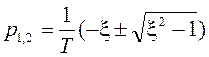(2.59.)

Следовательно, при значении ξ > 1 получим два действительных корня, значения которых будут меньше нуля, а при ξ < 1, получим два комплексно-сопряженных корня с отрицательной действительной частью, т.е. САУ будет устойчивой. Переходной процесс для комплексно-сопряженных корней в данном случае можно выразить в следующем виде:

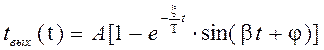(2.60.)

где

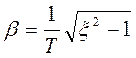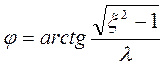; (2.61.)

ξ - коэффициент затухания, А – установившееся значение температуры при

выбранной величине управляющего параметра.

Запас устойчивости

С помощью запаса устойчивости – количественной характеристики удаления устойчивости определенной системы от границы устойчивости, производится оценка устойчивости системы. Обеспечение запаса устойчивости является необходимым условием, т.к. при линеаризации уравнений искажаются количественные характеристики системы, существует погрешность описания параметров звеньев, которые входят в коэффициенты уравнения, с течением времени внутренние параметры системы могут изменяться под действием температуры, режима эксплуатации, старения и других факторов. Запас устойчивости расширяет диапазон изменения внутренних параметров системы до определенных значений и более подробно характеризует переходные процессы в системе. С учетом того, каким критерием устойчивости пользуются при расчете, определяется запас устойчивости. Например, используя критерий Найквиста, согласно которого устойчивость системы зависит от того, охватывает ли АФЧХ системы на комплексной плоскости точку с координатами (-1; j0), при расчете запаса устойчивости оценивают степень удаления АФЧХ от указанной точки. Различают запасы устойчивости по амплитуде и по фазе.

Запас устойчивости по амплитуде (модулю) равен расстоянию h на действительной оси, между точкой (-1; j0) и ближайшей точкой пересечения годографа АФЧХ с этой же осью. Графическое представление запаса устойчивости по амплитуде изображено на рисунке 77.

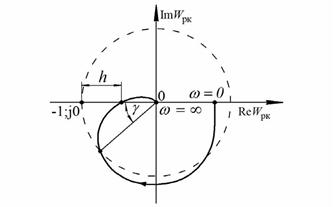
Рис.77. Графическое представление запаса устойчивости

В случае, если годограф АФЧХ имеет вид, изображенный на рисунке 78, запас устойчивости по модулю будет иметь два значения h₁ и h ₂,равных расстояниям от точки

(-1; j0) до ближайших точек пересечения годографа АФЧХ с действительной осью.

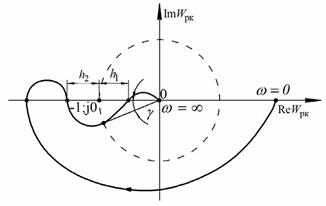
Рис.78. АФЧХ системы с двумя значениями запаса устойчивости

Запасом устойчивости по фазе называется угол γ, который образует отрицательная часть действительной оси и единичный радиус окружности с центром в точке начала координат, проходящий через точку пересечения годографа с данной окружностью.

Допустимый запас устойчивости при заданных величинах запаса устойчивости по модулю и по фазе, представляет собой сектор на комплексной плоскости, включающий точку (-1; j0) и ограниченный допусками ±h и ±γ, причем годограф АФЧХ в указанный сектор заходить не должен, как представлено на рисунке 79.

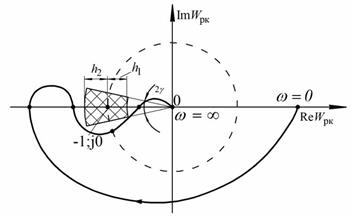
Рис.79. Графическое представление допустимого запаса устойчивости

Рассчитывая устойчивость САУ с использованием ЛЧХ, величину запаса устойчивости по модулю принимают соответствующей отрезкам l_i = 20 lg h_i, при тех значениях частоты ω, когда ЛФЧХ φ (ω) = −π, а величину запаса устойчивости по фазе принимают равной величине угла, представляющего превышение ЛФЧХ над уровнем −π при частоте ω_с (при L=0). Графическое представление запасов устойчивости по ЛЧХ приведены на рисунке 80.

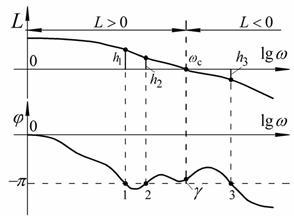
Рис.80. Запасы устойчивости САУ по ЛЧХ