Оптических системах

С развитием мощной лазерной техники, позволяющей создавать напряженности электрического поля в излучаемой волне более 10⁹ В/м появились возможности изучения дипольных моментов диэлектриков и других структур.

Поляризация диэлектриков приобретает сложный, нелинейный вид, которая описывается следующим выражением:

Р = e₀ (c₁Е + c₂Е² + c₃Е³ + … + c_nЕⁿ) (9.23)

Пусть плоская электромагнитная волна, совершает колебания по закону в направлении оси У:

Е = Е_m sin (wt – kу) (9.24)

и распространяется в некоторой среде по нелинейному закону

Р = e₀ (c₁Е + c₂Е²) (9.25)

После подстановки формулы (9.24) в формулу (9.25) и проведя некоторые преобразования, получим

Р = e₀ {(c₁ Е_m sin (wt – kу) + c₂ [Е_m sin (wt – kу)]²}

или

Р = e₀ [(c₁ Е_m sin (wt – kу) + c₂ Е²_m / 2 – c₂ Е²_m / 2 × cos (2wt – kу)]. (9.26)

Первое слагаемое в квадратных скобках описывает волну поляризации, синхронизированную с падающей волной.

Второе слагаемое – описывает существование статической поляризации (оптическое детектирование).

Третье слагаемое – описывает волну поляризации с двойной круговой частотой.

Так как фазовая скорость в волне поляризации с двойной круговой частотой не совпадает с фазовой скоростью падающей волны, то для генерации вторых гармоник первичные волны пропускаю через кристаллы, у которых имеются направления, где обе волны имеют одинаковые фазовые скорости.

Этот процесс называют волновой синхронизацией с передачей второй гармоники около 60% энергии.

Если в среде с квадратичной нелинейностью распространяются две волны, то согласно уравнений:

Е₁ = Е_m1 sin (w₁ t – k₁ у); (9.27)

Е₂ = Е_m2 sin (w₂ t – k₂ у). (9.28)

исходное электромагнитное поле имеет напряженность

Е = Е₁ + Е₂ . (7.38)

После подстановки формул: (9.27), (9.28) и (9.29) в (9.25) получим уравнение, в котором помимо появления статической поляризации возникают, в результате волновой синхронизации.

Вторые гармоники с круговыми частотами: (w₁ – w₂), (w₁ + w₂), т. е. наблюдается параметрическая генерация.

В связи с этим можно производить плавную перестройку частот из одного диапазона в другой.

А за счет параметрической генерации можно усиливать вторую волну с преобразованием частоты и получением энергии от волны накачки.

Если применить электромагнитные монохроматические волны, которые могут распространяться в среде с более высокой степенью нелинейности, например, кубической нелинейности вида:

Р = e₀ (c₁Е + c₃Е³),

то даже без учета третьей гармоники, при в ходе лучей в среду, волновые поверхности искривляются, происходит сжатие пучка и наступает явление самофокусировки света с большими плотностями энергии.

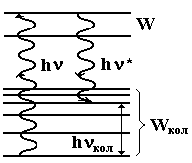
Если электроны в атомах и молекулах вещества могут совершать гармонические колебания, в системе колебательных подуровней (рис. 9.26) с энергией W_кол и набором собственных частот n_кол.

Фотоны первичной электромагнитной волны c энергией e = hn в веществе с частотой n, поглотившись электронами атомов, переводят их с основного уровня на возбужденные W.

По истечении некоторого времени (~10^-8 с) электроны переходят на один из колебательных подуровней W_кол, излучая квант (фотон) энергии e^* = hn^* рассеянного света с частотой n^*. Остальная часть энергии электрона соответствует его колебательной энергии W_кол с частотой n_кол.

Следовательно, в веществе существуют две волны с частотами n и n^*. Из-за нелинейности вещества при его взаимодействии с этими волнами возникают новые волны с частотами: (n – n^*) и (n + n^*). В нашем случае, существенна только эта частота (n – n^*) = n_кол. Электроны атомов вещества начинают совершать вынужденные колебания в резонансном режиме, излучая вторичные волны, с частотой n_кол.

Происходит усиление рассеянной волны.