Решения транспортных задач
Рассмотрим задачи информационной поддержки транспортировки продукции на примере дистрибьюторской фирмы сетевой структуры. Сетевые структуры дистрибьюторской фирмы являются прогрессивным направлением торговли и находят все большее применение в нашей стране.
Одним из примеров межрегиональной дистрибьюторской фирмы является ООО «Торговый Дом «ПЕКАР», обладающий 7 филиалами и выводящий на рынок автозапчастей новую номенклатуру товаров, составляющих от 8% до 12% в год.
Выведение на рынок новых товаров сопровождается неопределенным спросом на них. В условиях неопределенности спроса возникает задача обеспечения максимальной гарантированной прибыли. Распределение товара с неопределенным спросом осуществляется одновременно с устоявшимися товарами на рынке, характеризующимися случайным спросом с известными вероятностными характеристиками.
Специфика управления запасами межрегиональной дистрибьюторской фирмы состоит в том, что пополнение запасов осуществляется путем последовательного объезда транспортным средством всех филиалов с возможностью перераспределения неликвидного товара, так как неликвидный товар для одного филиала может являться «ходовым» для другого.
Случайный характер спроса требует заключения с поставщиками таких контрактов, которые позволяют в течение года адаптировать структуру заказов к интенсивности спроса. При этом должны быть согласованы интересы поставщиков и дистрибьюторской фирмы с учетом того, что продажа товара осуществляется от имени дистрибьюторской фирмы без указания производителя. Это обстоятельство с позиции интересов дистрибьюторской фирмы требует обеспечения необходимого уровня качества, цены и конкурентоспособности товара, а с позиции поставщиков – возможности диверсификации выбора торговых посредников путем соблюдения лимитов по объемам поставок.
В качестве примера сетевой структуры дистрибьюторской фирмы, рассматривается четырехуровневая сетевая структура межрегиональной дистрибьюторской фирмы ООО «Торговый Дом «ПЕКАР», г. Санкт-Петербург (рисунок 3.5).
Динамика выведения новых товаров на рынок показана в таблице 3.2.
Существующие модели и методы распределения товаров в сетевых структурах не в полной мере отражают особенности функционирования рассматриваемого класса межрегиональных торговых сетей.
Таблица 3.2.
Динамика выведения новых товаров на рынок автозапчастей
в дистрибьюторской фирме ООО «Торговый Дом «ПЕКАР»
в течение года
| Месяц | Количество выведенных новых товаров, шт. | Процент выведения новых товаров, % | Месяц | Количество выведенных новых товаров, шт. | Процент выведения новых товаров, % |
| Январь | 0,5% | Июль | 1,8% | ||
| Февраль | 0,5% | Август | 1,3% | ||
| Март | 1,0% | Сентябрь | 1,0% | ||
| Апрель | 1,5% | Октябрь | 1,0% | ||
| Май | 1,0% | Ноябрь | 0,8% | ||
| Июнь | 1,5% | Декабрь | 0,3% | ||
| ИТОГО за год | 12,0% |

Рис. 3.5. Четырехуровневая сетевая структура
межрегиональной дистрибьюторской фирмы
Предлагаемая логистическая информационная система ориентирована на учет этих особенностей.
Система математических моделей распределения товаров в торговой сети межрегиональной дистрибьюторской фирмы при случайном спросе представлена на рисунке 3.6.
Система моделей включает в себя три группы моделей:
· модели выбора структуры предложения филиала при неопределенном спросе;
· модели пополнения и перераспределения запасов при случайном спросе;
· модели выбора состава поставщиков товаров.

Рис. 3.6. Система моделей распределения товаров
в сети межрегиональной дистрибьюторской фирмы при случайном спросе
Предлагаемая система моделей охватывает все четыре уровня торговой сети, начиная от нижнего уровня, представленного потребителями товаров, включая третий уровень – филиалы торговой фирмы, второй уровень – дистрибьюторскую межрегиональную фирму и заканчивая верхним уровнем – поставщиками товаров в торговую сеть.
Система моделей предназначена для решения следующих задач:
- обоснования структуры предложения филиалов торговой фирмы при неопределенном спросе в условиях вывода новых товаров на рынок;
- обоснование объемов пополнения и перераспределения запасов в сети филиалов межрегиональной торговой фирмы при случайном спросе;
- расчета основных параметров управления запасами в межрегиональной сети, характеризующих стратегию управления запасами – оптимального общего для всех филиалов и постоянного периода пополнения и перераспределения запасов и размеров партий пополнения или изъятия излишков запасов филиалов при случайном спросе;
- обоснования выбора состава поставщиков товаров межрегиональной торговой фирмы в условиях предложения товаров покупателям от имени торговой фирмы без указания поставщиков (производителей) товаров.
Специфика постановки указанных задач характерна для торговых сетей межрегиональных дистрибьюторских фирм, в частности для дистрибьюторской фирмы ООО «Торговый Дом «ПЕКАР», работающей на рынке автозапчастей, на примере которой поставлены и решены указанные выше задачи.
Таким образом, сформированная система моделей охватывает все основные задачи, сопровождающие распределение товаров в торговой сети межрегиональной дистрибьюторской фирмы.
В условиях неопределенности спроса на новые товары, выводимые на рынок может быть применен теоретико-игровой подход. Предлагается использовать матричную игровую модель, имеющую вид:
 , (3.12)
, (3.12)
где  – прибыль филиала фирмы в случае продажи единицы товара
– прибыль филиала фирмы в случае продажи единицы товара  -го наименования;
-го наименования;  – издержки филиала в случае несовпадения предложения и спроса на единицу товара
– издержки филиала в случае несовпадения предложения и спроса на единицу товара  -го наименования;
-го наименования;  – количество наименований новых товаров.
– количество наименований новых товаров.
Прибыль филиала образуется за счет торговой наценки (надбавки) за вычетом торговых издержек за период пополнения и перераспределения товаров в торговой сети.
 , (3.13)
, (3.13)
где  – розничная цена единицы товара
– розничная цена единицы товара  -го наименования;
-го наименования;  – оптовая цена единицы товара
– оптовая цена единицы товара  -го наименования;
-го наименования;  – торговые издержки за период пополнения и перераспределения запасов
– торговые издержки за период пополнения и перераспределения запасов 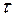 .
.
Платежная матрица модели является матрицей выигрыша первого игрока (филиала), играющего со вторым игроком (спросом). Эта матрица отражает особенности ценовой политики и торговых издержек региональных филиалов.
Специфика управления запасами в сетевой структуре состоит в том, что неликвидные товары изымаются. Поэтому торговые издержки отграничиваются периодом 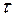 .
.
В состав торговых издержек включаются следующие статьи затрат: затраты на заработную плату персонала филиала: плата за кредит, используемый на оптовую закупку единицы товара; издержки, связанные с хранением и транспортировкой единицы товара; оплата посреднических услуг дистрибьюторской фирмы.
Структура игровой матрицы  такова, что в ней отсутствует «седловая точка», следовательно, оптимальными стратегиями игроков являются смешанные стратегии.
такова, что в ней отсутствует «седловая точка», следовательно, оптимальными стратегиями игроков являются смешанные стратегии.
Оптимальная стратегия первого игрока представлена вектором:
 , (3.14)
, (3.14)
где  – частота выбора
– частота выбора  -й частной стратегии первым игроком.
-й частной стратегии первым игроком.
Величины  , соответствуют структуре предложения новых товаров для обеспечения максимально возможной гарантированной прибыли в расчете на единицу товара.
, соответствуют структуре предложения новых товаров для обеспечения максимально возможной гарантированной прибыли в расчете на единицу товара.
Матричную игру целесообразно свести к задаче линейного программирования следующего вида:
 (3.15)
(3.15)
 (3.16)
(3.16)
 , (3.17)
, (3.17)
где  – переменная задачи линейного программирования, функционально связанная частотой
– переменная задачи линейного программирования, функционально связанная частотой  ;
;  – элемент платежной матрицы G, находящийся на пересечении
– элемент платежной матрицы G, находящийся на пересечении  -й строки и
-й строки и 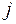 -го столбца.
-го столбца.
Переменная  связана с
связана с  соотношением
соотношением
 , (3.18)
, (3.18)
где  – цена игры, которая интерпретируется, как максимальная гарантированная прибыль в расчете на единицу товара в условиях неопределенного спроса.
– цена игры, которая интерпретируется, как максимальная гарантированная прибыль в расчете на единицу товара в условиях неопределенного спроса.
В биматричных моделях элементы матрицы представлены двумя числами или же имеются две матрицы, строки и столбцы в которой выбираются строго синхронно.
Если покупатели сталкиваются с дефицитом товара, то для филиала возникает так называемая «упущенная прибыль», поскольку покупатель не приобретает товар. Эта «упущенная прибыль» по абсолютной величине равна возможной прибыли в случае приобретения товара и противоположна по знаку. Упущенная прибыль возникает в данном планово-учетном периоде. Однако помимо нее наличие дефицита сказывается на потере спроса в последующих планово-учетных периодах, поскольку в следующий раз покупатель может предпочесть обратиться за покупкой в магазин конкурента.
Как упущенная прибыль, так и последующая потеря спроса не учитываются при расчете основного финансового результата деятельности (прибыли) хозяйствующего субъекта в данном периоде.
Оценка упущенной прибыли (и потери спроса) могут быть осуществлены параллельно с оценкой гарантированной прибыли путем добавления второй матрицы в теоретико-игровую модель.
Совокупность ранее рассмотренной матрицы для оценки гарантированной прибыли и матрицы «упущенной прибыли» образует биматричную модель оценки структуры предложения с учетом полученной и упущенной прибыли.
Биматричная модель формируется путем добавления к матрице  , матрицы упущенной прибыли
, матрицы упущенной прибыли  , имеющей следующий вид:
, имеющей следующий вид:
 . (3.19)
. (3.19)
Для нахождения среднего значения упущенной прибыли в расчете на единицу товара при оптимальных стратегиях первого и второго игроков в соответствии с матрицей  по критерию максимизации гарантированной прибыли, необходимо решить двойственную задачу линейного программирования применительно к матрице
по критерию максимизации гарантированной прибыли, необходимо решить двойственную задачу линейного программирования применительно к матрице  . Эта задача имеет вид:
. Эта задача имеет вид:
 (3.20)
(3.20)
 (3.21)
(3.21)
 , (3.22)
, (3.22)
где  – частота выбора
– частота выбора 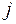 -й чистой стратегии вторым игроком по матрице
-й чистой стратегии вторым игроком по матрице  .
.
Переменные двойственной задачи  связаны с частотами выбора частных стратегий вторым игроком следующими соотношениями:
связаны с частотами выбора частных стратегий вторым игроком следующими соотношениями:
 . (3.23)
. (3.23)
При этом оптимальная смешанная стратегия второго игрока представлена вектором
 . (3.24)
. (3.24)
Средняя упущенная прибыль в расчете на единицу товара составляет величину:
 , (3.25)
, (3.25)
где  элемент матрицы
элемент матрицы  , находящейся на пересечение
, находящейся на пересечение  -й строки и
-й строки и 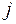 -го столбца.
-го столбца.
Периодическое синхронное пополнение запасов, предлагаемое для сетевой структуры торговой фирмы, обеспечивает возможность перераспределения запасов с целью изъятия неликвидных остатков.
Пополнение запасов в торговой сети фирмы предполагает формирование максимального запаса товаров в каждом филиале к началу планового периода с учетом средней прогнозируемой интенсивности спроса и страхового запаса на случай превышения интенсивности спроса над средней величиной и возможного запаздывания срока пополнения запасов.
Взаимосвязь основных параметров управления запасами в торговой сети представлена на рисунке 3.7.
На рисунке приняты следующие обозначения:  – время;
– время;  – количество товара на складе филиала;
– количество товара на складе филиала; 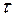 – период пополнения запаса;
– период пополнения запаса;  – максимальное время запаздывания поставки товаров на филиал по сравнению с плановым сроком;
– максимальное время запаздывания поставки товаров на филиал по сравнению с плановым сроком;  – ожидаемая (средняя) интенсивность продаж товара данного наименования на
– ожидаемая (средняя) интенсивность продаж товара данного наименования на  -м филиале (количество единиц товара, проданных за сутки);
-м филиале (количество единиц товара, проданных за сутки);  – максимальная прогнозируемая интенсивность продаж товара данного наименования на
– максимальная прогнозируемая интенсивность продаж товара данного наименования на  -м филиале;
-м филиале;  – максимальная величина запаса
– максимальная величина запаса  -го филиала;
-го филиала;  – основной запас
– основной запас  -го филиала;
-го филиала;  – величина страхового запаса товаров на
– величина страхового запаса товаров на  -м филиале;
-м филиале;  – страховой запас
– страховой запас  -го филиала, рассчитанный на увеличение интенсивности продаж по сравнению со средней величиной до прогнозируемой максимальной интенсивности продаж при соблюдении планового срока пополнения запаса;
-го филиала, рассчитанный на увеличение интенсивности продаж по сравнению со средней величиной до прогнозируемой максимальной интенсивности продаж при соблюдении планового срока пополнения запаса;  – страховой запас
– страховой запас  -го филиала, рассчитанный на максимальное время запаздывания поставки при максимальной интенсивности спроса.
-го филиала, рассчитанный на максимальное время запаздывания поставки при максимальной интенсивности спроса.
 |
Рис. 3.7. Взаимосвязь основных параметров управления
запасами филиалов торговой фирмы при случайном спросе
Построение модели расчета оптимального периода пополнения и перераспределения запасов в смысле минимизации логистических издержек состоит в нахождение такого значения  , которое обращает в ноль производную суммарных логистических издержек в сетевой структуре:
, которое обращает в ноль производную суммарных логистических издержек в сетевой структуре:
 , (3.26)
, (3.26)
где 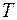 – продолжительность года (в количестве суток);
– продолжительность года (в количестве суток);  – транспортные затраты на однократный объезд филиалов сети;
– транспортные затраты на однократный объезд филиалов сети;  – средневзвешенные по номенклатуре товаров затраты на хранение единицы товара на складе филиала в единицу времени (сутки);
– средневзвешенные по номенклатуре товаров затраты на хранение единицы товара на складе филиала в единицу времени (сутки);  – максимальное время запаздывания поставки товаров, выраженное в долях периода пополнения запаса;
– максимальное время запаздывания поставки товаров, выраженное в долях периода пополнения запаса;  – ожидаемая (средняя) интенсивность продаж в сетевой структуре (в сумме по номенклатуре товаров и филиалам);
– ожидаемая (средняя) интенсивность продаж в сетевой структуре (в сумме по номенклатуре товаров и филиалам);  – максимальная прогнозируемая интенсивность продаж в сетевой структуре.
– максимальная прогнозируемая интенсивность продаж в сетевой структуре.
Оптимальный период пополнения и перераспределения запасов филиалов при этом составляет величину (в сутках):
 (3.26)
(3.26)
При  и
и  предлагаемая здесь формула (3.26) обращается в известную формулу Уилсона (см. п. 3.5).
предлагаемая здесь формула (3.26) обращается в известную формулу Уилсона (см. п. 3.5).
Транспортная задача пополнения и перераспределения запасов филиалов в сети межрегиональной дистрибьюторской фирмы, отличается тем, что в ней учитываются как оптимальная последовательность объезда филиалов, так и возможность не только увеличения запасов, но и изъятия излишков при случайном спросе.
Решению поставленной закрытой транспортной задачи должно предшествовать установление оптимальной последовательности объезда транспортным средством филиалов межрегиональной торговой сети с применением известной модели «коммивояжера», а также получение прогнозных значений на предстоящий период средней и максимальной потребности и переходящих остатков товаров в разрезе филиалов и наименований товаров, что необходимо для расчета размеров партий пополнения или изъятия запасов.
Содержательная постановка задачи «коммивояжера» состоит в нахождении минимального по расстоянию движения фуры, перевозящей товары, которой начинается и заканчивается в месте расположения дистрибьюторской фирмы (центрального склада) и проходит через все филиалы торговой сети фирмы.
Математическая модель задачи:
 (3.27)
(3.27)
 (3.28)
(3.28)
 (3.29)
(3.29)
 , (3.30)
, (3.30)
где  – длина пути между населенными пунктами
– длина пути между населенными пунктами  и
и  ;
;  – множество населенных пунктов, охваченных торговой сетью фирмы, включая населенный пункт, в котором находится центральный склад фирмы, и все филиалы;
– множество населенных пунктов, охваченных торговой сетью фирмы, включая населенный пункт, в котором находится центральный склад фирмы, и все филиалы;  – наименование пункта выезда фуры;
– наименование пункта выезда фуры;  – наименование пункта въезда фуры;
– наименование пункта въезда фуры;  – двоичная переменная, принимающая значение 1, если из пункта
– двоичная переменная, принимающая значение 1, если из пункта  фура переезжает в пункт
фура переезжает в пункт  , и 0 – в противном случае;
, и 0 – в противном случае;  – суммарная длина маршрута фуры, которая начинается и заканчивается в географическом месте расположения центрального склада дистрибьюторской фирмы.
– суммарная длина маршрута фуры, которая начинается и заканчивается в географическом месте расположения центрального склада дистрибьюторской фирмы.
Условия (3.28) и (3.29) соответственно обеспечивают однократность выезда и въезда в каждый населенный пункт торговой сети межрегиональной дистрибьюторской фирмы.
Методы прогнозирования спроса, как известно, подразделяются на качественные и количественные. К качественным методам относятся метод Дельфи, метод «мозговой атаки» и др. К количественным методам относятся прогнозная модель скользящей средней, метод экспоненциального сглаживания, однофакторная линейная регрессионная модель, метод стабилизации и др.
Выбор конкретной прогнозной модели и количественных значений ее параметров определяется в общем случае путем проведения прогнозных расчетов на типичных динамиках реализации хранимых номенклатур.
Математическая постановка транспортной задачи имеет вид:
 (3.31)
(3.31)
 (3.32)
(3.32)
 (3.33)
(3.33)
 (3.34)
(3.34)
Здесь приняты следующие обозначения:  – стоимостные затраты, связанные с пополнением и перераспределением товара в сетевой структуре;
– стоимостные затраты, связанные с пополнением и перераспределением товара в сетевой структуре;  – количество товаров, доставляемого из
– количество товаров, доставляемого из  -го пункта отправления (из филиала или центрального склада) в
-го пункта отправления (из филиала или центрального склада) в  -й пункт назначения (филиал);
-й пункт назначения (филиал);  – длина пути между
– длина пути между  -м пунктом отправления и
-м пунктом отправления и  -м пунктом назначения при однонаправленном движении по маршруту объезда филиалов сети;
-м пунктом назначения при однонаправленном движении по маршруту объезда филиалов сети;  – удельные транспортные издержки в расчете на единицу товара заданного наименования и единицу расстояния;
– удельные транспортные издержки в расчете на единицу товара заданного наименования и единицу расстояния;  – потребность пополнения запасов
– потребность пополнения запасов  -го филиала;
-го филиала;  – потенциальная возможность поставки товара
– потенциальная возможность поставки товара  -м пунктом отправления;
-м пунктом отправления;  – множество поставщиков товара, включая центральный склад и филиалы сети;
– множество поставщиков товара, включая центральный склад и филиалы сети;  – множество филиалов сети, нуждающихся в пополнении запасов.
– множество филиалов сети, нуждающихся в пополнении запасов.
Транспортная задача должна решаться для каждого наименования товара перед каждым периодом пополнения запасов.
Особенностью организации торговли крупной межрегиональной торговой фирмы на рынке автозапчастей является присвоение товару торговой марки фирмы без указания производителя товара. Эта особенность повышает узнаваемость и конкурентоспособность товаров торговой сети фирмы при условии обеспечения высокого качества предлагаемых товаров. Гарантия высокого качества возлагается в этих условиях на торговую фирму, а не на поставщиков товара. Однако, с другой стороны, эта особенность организации торговли делает зависимым производителей товаров от торгового посредника.
Модели выбора состава поставщиков товаров межрегиональной торговой фирмы используют результаты прогнозирования спроса на среднесрочный период (год) и оптимальную структуру предложения в условиях неопределенности спроса с учетом номенклатуры и количества товаров каждого наименования. Эти модели представлены в двух вариантах – модель выбора нескольких поставщиков товара для каждого наименования и модель выбора одного поставщика товара каждого наименования. Каждая модель имеет свою область применения в зависимости от условий работы дистрибьюторской фирмы.
Модель задачи оптимального выбора производителей товаров для случая, когда товар одного наименования может поставляться несколькими производителями, имеет вид:
 (3.35)
(3.35)
 (3.36)
(3.36)
 (3.37)
(3.37)
 (3.38)
(3.38)
 (3.39)
(3.39)
 (3.40)
(3.40)
 (3.41)
(3.41)
Здесь приняты следующие обозначения:  – количество товаров
– количество товаров  -го наименования, поставляемых
-го наименования, поставляемых  -м производителем (искомая переменная);
-м производителем (искомая переменная);  – прибыль от реализации торговой фирмой единицы товара
– прибыль от реализации торговой фирмой единицы товара  -го наименования, полученной от
-го наименования, полученной от  -го производителя;
-го производителя;  – оптовая цена за единицу товара
– оптовая цена за единицу товара  -го наименования в случае поставки от
-го наименования в случае поставки от  -го производителя;
-го производителя;  – лимит, устанавливаемый
– лимит, устанавливаемый  -м производителем, для торговых сделок с данной торговой фирмой в сумме по всей номенклатуре товаров;
-м производителем, для торговых сделок с данной торговой фирмой в сумме по всей номенклатуре товаров;  – лимит финансовых возможностей торговой фирмы в сумме по всем заключенным контрактам;
– лимит финансовых возможностей торговой фирмы в сумме по всем заключенным контрактам;  – общее количество единиц товаров, поставляемых в сумме по всем контрактам торговой фирмы;
– общее количество единиц товаров, поставляемых в сумме по всем контрактам торговой фирмы;  – допустимое (минимальное) интегральное значение коэффициента конкурентоспособности товаров торговой фирмы (устанавливаемый фирмой уровень конкурентоспособности товаров);
– допустимое (минимальное) интегральное значение коэффициента конкурентоспособности товаров торговой фирмы (устанавливаемый фирмой уровень конкурентоспособности товаров);  – интегральный показатель качества товаров
– интегральный показатель качества товаров  -го наименования, обеспечиваемого
-го наименования, обеспечиваемого  -м поставщиком продукции;
-м поставщиком продукции;  – допустимое (минимальное) интегральное значение показателя качества товаров торговой фирмы (устанавливаемый фирмой уровень качества товаров);
– допустимое (минимальное) интегральное значение показателя качества товаров торговой фирмы (устанавливаемый фирмой уровень качества товаров);  – множество наименований товаров;
– множество наименований товаров;  – множество поставщиков товаров.
– множество поставщиков товаров.
Экономический смысл целевой функции и ограничений следующий.
Целевая функция (3.35) предусматривает максимизацию годовой прибыли дистрибьюторской торговой фирмы, выполняющей посреднические функции между производителями (поставщиками) товаров и розничными покупателями в рамках межрегиональной торговой сети.
Ограничение (3.36) обеспечивает диверсификацию в торговле производителя в части выбора торговых посредников на оптовом рынке и необходимый для производителя уровень независимости от отдельных торговых посредников.
Ограничение (3.37) обеспечивает распределение финансовых ресурсов торговой фирмы между поставщиками товаров при заключении контрактов в рамках имеющегося лимита.
Ограничения (3.38) и (3.39) соответственно характеризуют необходимый уровень конкурентоспособности и качества товаров торговой фирмы в целом, то есть бренд торговой марки межрегиональной торговой фирмы.
Ограничение (3.40) обеспечивает поставку товаров в необходимом для торговой фирмы количестве.
Вторая постановка задачи, при которой один поставщик закрепляется за одним наименованием товара, имеет следующий вид:
 (3.42)
(3.42)
 (3.43)
(3.43)
 (3.44)
(3.44)
 (3.45)
(3.45)
 (3.46)
(3.46)
 (3.47)
(3.47)
 (3.48)
(3.48)
Здесь  представляет собой двоичную переменную, принимающую значение 1, если
представляет собой двоичную переменную, принимающую значение 1, если  -й поставщик выбран для поставки товара
-й поставщик выбран для поставки товара  -го наименования, и 0 – в противном случае.
-го наименования, и 0 – в противном случае.
С вычислительной точки зрения первая постановка задачи намного проще. С организационно-экономической точки зрения эта поставка является более гибкой, в частности имеет то преимущество, что повышает надежность поставок за счет диверсификации поставщиков.
Однако вторая постановка позволяет продавать товар каждого наименования однородный по качеству и конкурентоспособности.
Окончательное принятие решения в пользу той или иной постановки задачи выбора поставщиков товаров требует привлечения дополнительной информации, характеризующей условия хозяйствования торговой фирмы.
Например, межрегиональная дистрибьюторская фирма ООО «Торговый Дом «ПЕКАР», работающая на рынке автозапчастей, считает предпочтительным использование первой постановки задачи.
Важной особенностью заключения контрактов торговой фирмой с поставщиками товаров при случайном характере спроса является возможность изменять в течение года структуру поставок в определенных пределах при сохранении общего объема поставок в денежном выражении.
Рассмотренные модели системы распределения товаров по филиалам дистрибьюторской фирмы, относятся к классу моделей математического программирования. Исследование этих моделей поддерживается такими программными средствами, как MATLAB, Microsoft Excel, WINQSB и др.
Программное средство MATLAB характеризуется относительно сложным и архаичным интерфейсом, хотя ценится профессионалами за огромный набор функций.
Программное средство Microsoft Excel имеет надстройку «Поиск решения», которую удобно использовать для решения непрерывных задач. Для решения задач с двоичными переменными относительно большой размерности более эффективен пакет программ WINQSB.
Программные средства WINQSB – это набор программ, с помощью которого можно «проигрывать» различные варианты решения экономических и производственных задач, выявлять оптимальные из них и анализировать полученные результаты, используя различные методы.
К основным программам WINQSB относятся программы решения задач линейного программирования, целочисленного программирования, транспортных задач, задачи о назначении, сетевого моделирования, динамического программирования, управления запасами, теории очередей, имитационного моделирования, дисперсионного и байесовского анализа, анализа платежной матрицы и дерева решений, марковских моделей, экстраполяционных тенденций.
Таким образом, функциональные возможности программных продуктов WINQSB соответствуют потребностям решения задач в системе распределения товаров по филиалам дистрибьюторской фирмы. Экспериментальные расчеты по моделям с помощью этого пакета и практика использования результатов расчетов на ряде филиалов подтвердили адекватность моделей условиям межрегиональной дистрибьюторской фирмы.
Эффективность применения предлагаемой системы моделей основывается на согласовании интересов хозяйствующих субъектов на рынке дистрибьюторской фирмы и состоит в повышении прибыли дистрибьюторской фирмы и ее филиалов, сокращении логистических издержек, обновлении ассортимента, повышении качества и снижении розничной цены товаров.
Дата добавления: 2016-02-04; просмотров: 1240;
