Электронограммы монокристаллов
Геометрия возникновения дифракционной картины в случае электронных волн принципиально аналогична случаю рентгеновской дифракции. Особенности возникают из-за малой длины волны электронов. Для построения дифракционной картины от неподвижного монокристалла, воспользуемся, как всегда обратной решеткой и сферой отражения (будем рассматривать случай “на просвет”). При чрезвычайно малых длинах волн электронных пучков радиус сферы отражения 1/lэл очень велик – сфера вырождается практически в плоскость (рис.6.2).Поэтому возможность пересечения ее с узлами обратной решетки много больше. На электронограмме в этом случае появится множество рефлексов.
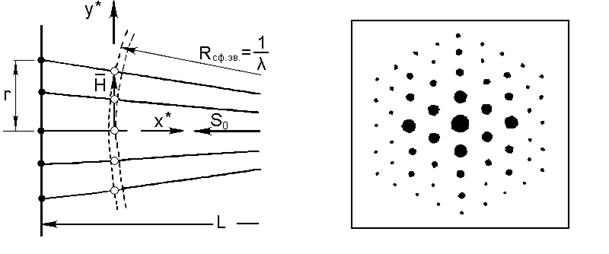
| Рис.6.2. Проектирование обратной решетки на фотопластинку электронным лучом. | Рис.6.3. Электронограмма монокристалла. |
Возможность пересечения сферы отражения с узлами обратной решетки увеличивается также и в силу мозаичного строения кристаллов, что приводит к превращению узлов обратной решетки из точек в небольшие участки сферы. Распределение плотности по этим участкам может быть как равномерным, так и неравномерным, поскольку оно отражает функцию распределения кристаллов по углам. Тепловые колебания решетки, также дают размытие узлов обратной решетки. Кроме того, пучок электронов из-за колебания напряжения на электронографе может иметь не совсем постоянную l. Это приводит к размытию самой сферы Эвальда и также увеличивает число интерференционных пятен на электронограмме. Последние два обстоятельства приводят, конечно, к неточности определения l и ухудшению четкости дифракционной картины.
Согласно рис.6.3 на электронограмме возникает серия пятен, которые в некотором масштабе изображают плоскость обратной решетки, т.е. электронограмма является как бы проекцией слоя обратной решетки, перпендикулярной к лучу. Такая электронограмма называется точечной.
По положению пятен дифракции можно определить межплоскостные расстояния d для системы отражающих плоскостей. Если расстояние между данным пятном электронограммы и следом первичного пучка r (рис.6.2), а между образцом и пленкой L, то можно записать
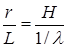 , (6.8)
, (6.8)
если r||H, что допустимо при очень малой кривизне сферы Эвальда. Радиус вектор обратной решетки по величине равен H=1/d. Поэтому можем переписать выражение (6.8) как
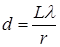 , (6.9)
, (6.9)
В последнем выражении точность определения d будет зависеть от точности замера L и l. Замерить эти величины на электронографе с большой степенью точности трудно, поэтому предварительно снимают эталон-кристалл с известным межплоскостным расстоянием. Для него вычисляют величину Ll, равную dэтал×r. Значение Ll носит название постоянной электронографа и используется в последующих расчетах.
Для примера:
L=700 мм; l=0,05 Å; Ll =35 Å×мм. Если измерять r в мм, то d получим в Å. Соответственно величина Ll и является масштабом. 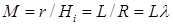 .
.
Таким образом, в приведенном примере Ll=35 Å·мм означает M=35 Å·мм, т.е. в масштабе пластинки 35 мм соответствует расстоянию в 1 Å в обратной решетке, а значит d*=0,2Å из предыдущего примера на электронограмме будет соответствовать 7 мм.
Дата добавления: 2016-02-04; просмотров: 2029;
