Символика Бравэ. Ячейки Бравэ.

Рассматривая деление кристаллов на сингонии, мы учитывали только форму элементарной ячейки. Однако в одной сингонии могут существовать различные по симметрии ячейки. Они отличаются по расположению узлов. В том случае, когда узлы располагаются только в вершинах элементарного параллелепипеда, мы имеем примитивную P ячейку (рис.1.7). При расположении узлов в вершинах и в центре объема – объемноцентрированную ячейку I. Если узлы располагаются в вершинах и в центре всех граней - гранецентрированную F, или в центрах одной пары двух противоположных граней - базоцентрированные ячейки. В зависимости от того, какие пары граней центрированные, базоцентрированные ячейки обозначаются буквами A, B и C.

Возможное число элементарных ячеек, отличающихся между собой своей симметрией, было впервые определено Бравэ. При этом он сформулировал три условия, которые позволяют из бесконечного числа параллелепипедов в пространственной решетке выбрать один, однозначно определяющий элементарную ячейку. Эти условия следующие:

1) сингония элементарной ячейки должна быть такой же, как и сингония всей системы в целом;

2) число прямых углов между ребрами элементарной ячейки должно быть максимальным;

3) при выполнении первых двух условий объем элементарной ячейки должен быть минимальным.

Если рассмотреть эти правила Бравэ на примере двухмерной пространственной сетки (рис.1.8), то становится ясным, что из трех заштрихованных, мы должны выбрать как элементарную ячейку одну - квадрат, минимальный по размеру.

Испытывая примитивную ячейку каждой сингонии на возможность и присутствие в ней дополнительных узлов в центрах граней или объема, получим согласно этим правилам все возможные ячейки Бравэ. Так, для ромбической сингонии мы, помещая узлы в центре граней и объема, получим, кроме примитивной ячейки, еще три (рис.1.7). Эти четыре решетки неэквивалентны, точнее в их объеме нельзя выделить меньшую элементарную ячейку, которая имела бы ту же сингонию.

Наличие дополнительных узлов в центрах граней и объема не меняет сингонию решетки, поэтому мы рассмотренными выше четырьмя случаями исчерпали все возможные ромбические решетки.

Для других сингоний в ряде случаев это возможно. Например, в тетрагональной сингонии введением дополнительных узлов в центры объема и граней можно получить только одну дополнительную, кроме примитивной, ячейку. Это объемноцентрированная ячейка. Базоцентрированная тетрагональная решетка сводится к примитивной. Это легко показать (рис.1.9). Здесь x¢, y¢ - старые оси; x, y - новые оси, которые выбираются под 45° к старым осям. Из построения рис.1.9 видно, что за элементарную ячейку в пространственной сетке, построенной путем бесконечного повторения старой ячейки С (в данном случае для этого достаточно рассмотреть всего лишь две базоцентрированные ячейки), следует принять новую ячейку P. Эта ячейка имеет ту же сингонию, но вдвое меньше по объему. Новая ячейка является примитивной. Таким образом, базоцентрированная ячейка сводится к примитивной.

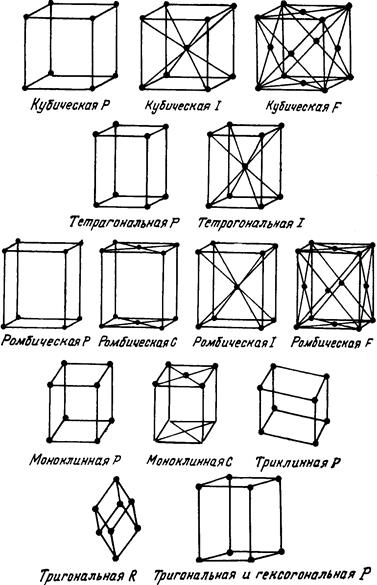
Рис.1.7. Решетки Бравэ.

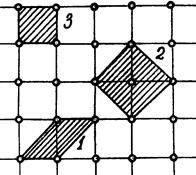
Рис.1.8. Выбор элементарной ячейки.

Точно таким же способом доказывается тождество гранецентрированной тетрагональной ячейки с объемноцентрированной.

Рассматривая подобным образом элементарные ячейки всех сингоний, получим, что в триклинной сингонии возможна только примитивная ячейка P, в моноклинной - P и C, в ромбической - P, C, I, F, в ромбоэдрической - P, в тетрагональной - P и I, в гексагональной - P и в кубической - P, I, F. Всего 14 ячеек Бравэ (рис.1.7).

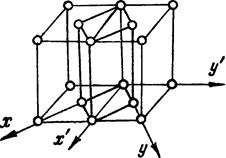
Рис.1.9. Замена базоцентрированной тетрагональной ячейки примитивной.

Каждый тип решеток Бравэ, являясь элементарной ячейкой пространственной решетки, представляет некоторый набор трансляций, посредством которого можно деталь структуры переносить параллельно самой себе, образуя в пространстве трехмерный узор кристалла. Каждое рентгеновское исследование начинается с определения размеров и типа решетки Бравэ.