ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ

В инженерной практике часто приходится встречаться с истечением жидкости из сосудов через отверстия различных форм и размеров и через различные короткие патрубки, называемые насадками.

При этом истечение может происходить в атмосферу, или в газообразную среду, или под уровень (затопленное отверстие) при постоянном или переменном напоре.

Отверстием в тонкой стенке называется такое отверстие, края которого имеют острую кромку, а толщина стенки не влияет на форму и условия истечения струи. Следовательно, жидкость, протекающая через такое отверстие, имеет только местные потери энергии, аналогичные потерям энергии при внезапном сужении потока.

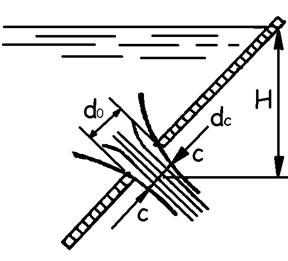
Боковое отверстие считается малым, если его вертикальный размер не превышает 0,1 напора, т.е. d₀ < 0,1H (рис. 9.1). В противном случае отверстие называется большим. У нижнего края такого отверстия напор будет значительно больше напора у верхнего края, а значит, будут разными скорости истечения по высоте. Очевидно, у донного отверстия, независимо от его размеров, напор во всех точках одинаков.

Особенность истечения жидкости через отверстия состоит в том, что на некотором расстоянии от стенки ( 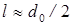) образуется сжатое сечение струи С-С (рис. 9.1). В сжатом сечении наблюдается параллельно-струйное движение со скоростью, превышающей скорость выхода жидкости из отверстия.

При установившемся истечении жидкости при постоянном напоре (H =const) из большого открытого резервуара через малое отверстие средняя скорость в сжатом сечении струи по уравнению Д. Бернулли равна

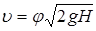, (9.1)

где H - глубина центра тяжести сжатого сечения струи под уровнем (напор истечения); 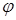- безразмерный коэффициент скорости, определяемый из выражения

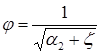, (9.2)

где 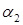- коэффициент кинетической энергии в сжатом сечении струи; 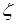- коэффициент сопротивления отверстия, выражающий потерю напора при истечении в долях скоростного напора струи.

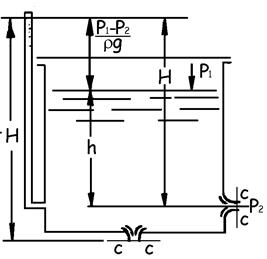
В общем случае истечения из замкнутого резервуара в газообразную среду (рис. 9.2) напор истечения H определяется как разность гидростатических напоров в резервуаре и в центре сечения струи

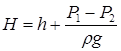, (9.3)

где h - глубина центра сжатого сечения струи под уровнем жидкости; Р₁ - давление в резервуаре на свободную поверхность жидкости; Р₂ - давление среды, в которую вытекает струя.

Степень сжатия струи, вытекающей через отверстие, характеризуется коэффициентом сжатия

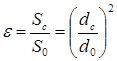, (9.4)

где S₀ и d₀ - площадь сечения и диаметр отверстия; S_с и d_с - площадь и диаметр сжатого сечения струи.

Объемный расход жидкости через отверстие определяется по зависимости

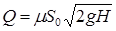, (9.5)

где 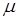- коэффициент расхода, равный

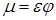(9.6)

Значения коэффициентов истечения 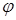, 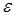и 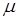зависят от формы и размеров отверстия, условий подтока жидкости к отверстию и числа Рейнольдса, определяемого выражением

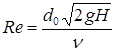, (9.7)

где 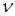- кинематический коэффициент вязкости жидкости.

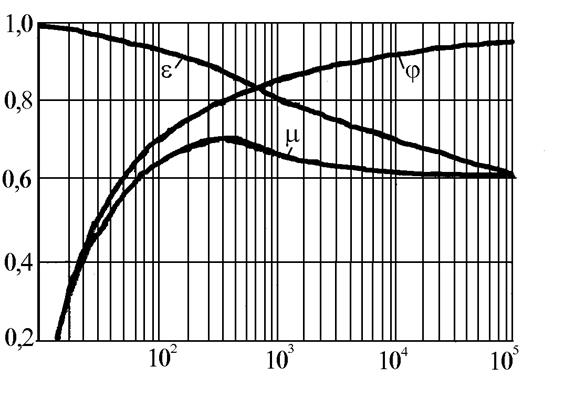
Зависимость коэффициентов истечения от Re для малого круглого отверстия с острой кромкой показана (по данным А.Д. Альтшуля) на рис. 9.3.

Увеличение коэффициента сжатия струи e с уменьшением Re объясняется тем, что возрастающее влияние сил вязкости ведет к утолщению заторможенного (пограничного) слоя у стенок и, следовательно, к уменьшению скоростей частиц жидкости, подтекающих сбоку к отверстию.

При уменьшении числа Рейнольдса возрастает неравномерность распределения скоростей в начальном сечении струи и увеличивается потеря напора, вызываемая касательными напряжениями трения в пограничном слое. Увеличение коэффициента кинетической энергии α₂ и коэффициента сопротивления ζ влечет за собой уменьшение коэффициента скорости φ.

Опыт показывает, что при Re > 10⁵ влияние Re на коэффициенты истечения практически отсутствует (квадратичная зона истечения). В этой области для расчетов можно пользоваться следующими их средними значениями φ=0,97; ε=0,62; μ=0,60. При этом неравномерность скоростей в сжатом сечении невелика и a₂=1, а найденный из выражения (9.2) коэффициент сопротивления отверстия z=0,06.

В этой области для малых отверстий других форм можно принимать μ=0,60.

В случае истечения под уровень для его расчета также можно пользоваться формулами (9.1) и (9.6), принимая значения коэффициентов истечения такими, как и при истечении в атмосферу. Напор истечения в этом случае представляет разность гидростатических напоров в резервуарах над центром отверстия.

Аналогично рассчитывается процесс истечения через большое отверстие. Однако коэффициент расхода μ в этом случае несколько больше и находится в пределах 0,60 ¸ 0,65 в зависимости от отношения H/d₀.

В отличие от отверстий насадки представляют собой короткие патрубки (l=(2¸3)d₀), присоединенные к отверстию в тонкой стенке.

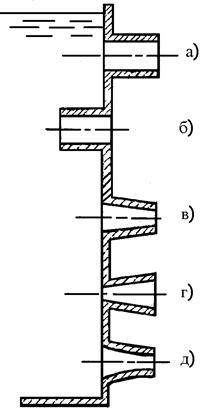
Насадки разделяются на три основные типа (рис. 9.4): цилиндрические, конические и коноидальные. Цилиндрические насадки бывают внешние (рис. 9.4, а) и внутренние (рис. 9.4, б). Они предназначаются для опорожнения резервуаров. Конические насадки бывают расходящиеся (рис. 9.4, г), предназначаемые для уменьшения выходной скорости (например, в дождевальных аппаратах), и сходящиеся (рис. 9.4, в), предназначаемые для создания компактной струи с большой выходной скоростью (например, в пожарных брандспойтах, гидромониторах и т.п.). Коноидальные насадки (рис. 9.4, д), выполняемые по форме струи, вытекающей из отверстия, обеспечивают минимальные потери энергии и имеют то же назначение, что и сходящийся конический насадок. Максимальный коэффициент расхода в конических сходящихся насадках соответствует углу конусности 13⁰ 24'.

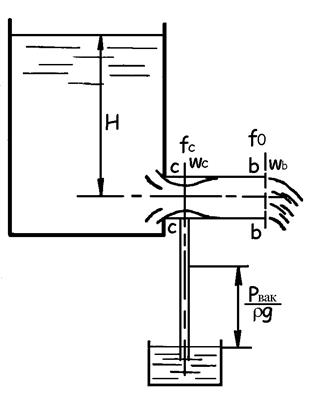
При истечении жидкости через насадок в атмосферу, а также в равной мере через отверстие в толстой стенке внутри насадка в сжатом сечении, образуется вакуум. Это объясняется тем, что в сжатом сечении С-С (рис. 9.5) скорости больше, чем при выходе из насадка (u_с > u_в), а потому (по уравнению Д. Бернулли) давление в сжатом сечении будет меньше атмосферного (P_с < P_ат). В связи с этим происходит как бы “подсасывание” жидкости.

При истечении жидкости при постоянном напоре через насадки скорость на выходе из насадка и расход определяются по формулам (9.1) и (9.5). В данных зависимостях S₀ - является выходной площадью насадка. Причем, напор берется для центра выходного сечения. Значения коэффициентов истечения зависят от геометрии и расположения насадка, от напора, и для основных типов насадков в квадратичной зоне их средние значения приведены в приложении 4.

Большая величина коэффициента расхода, т.е. пропускной способности цилиндрического насадка по сравнению с отверстием такого же диаметра объясняется наличием внутри насадка вакуума и отсутствием сжатия струи на выходе.

Вакуум в сжатом сечении пропорционален напору. Это значит, что при некотором напоре H вакуум может стать настолько большим, что начнется кавитация жидкости в сжатом сечении. При интенсивном развитии кавитации происходит отрыв струи от внутренних стенок насадка, и истечение через насадок сменяется истечением через отверстие. Напор, при котором происходит срыв струи, называется предельным напором H_пр. Обычно H_пр=13 м для цилиндрического насадка. Для конических расходящихся насадков значение H_пр будет меньше и зависит от угла конусности.

То, что наибольший коэффициент расхода у коноидального насадка, объясняется формой этого насадка, которая обеспечивает наименьшие потери энергии струи при ее прохождении через насадок.

Истечение при переменном напоре имеет место при полном или частичном опорожнении резервуаров.

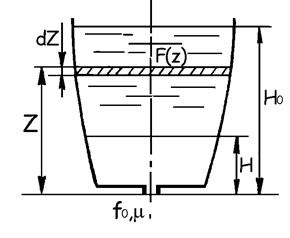
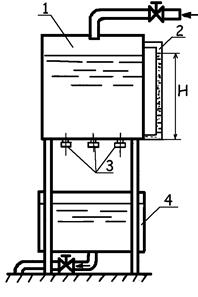
Дифференциальное уравнение процесса опорожнения открытого резервуара произвольной формы при отсутствии притока в него жидкости (рис. 9.6) имеет вид

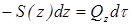, (9.8)

где Q_z - расход жидкости через выходное отверстие при текущем значении напора z; S(z) - площадь свободной поверхности жидкости в резервуаре как функция напора z; dz - понижение уровня в резервуаре за время .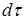

Мгновенный расход Q_z при этом определяется по формуле

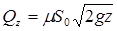, (9.9)

где 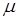- коэффициент расхода выпускного устройства, отнесенный к выходному сечению площадью S₀.

При квадратичном режиме истечения, который чаще всего наблюдается для маловязких жидкостей, коэффициент расхода принимается постоянным в течение всего процесса. Тогда интеграл уравнения (9.8), дающий время опорожнения резервуара от начального уровня H₀ до произвольного H, имеет вид

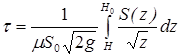(9.10)

Для призматического резервуара, у которого S(z) = S = const, уравнение (9.10) имеет вид

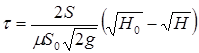(9.11)

Если опорожнение происходит через ряд совместно работающих выпускных устройств, то в уравнении (9.8) Q_z - есть суммарный объемный расход жидкости из резервуара.

Цель работы- опытным путем определить коэффициенты расхода при истечении жидкости через отверстие в тонкой стенке, цилиндрический, конический и коноидальный насадки при постоянном напоре и сравнить их с литературными данными. Измерить время частичного опорожнения резервуара и сравнить его с теоретическим.