Теория волн для глубокого моря (трохоидальная теория)

Величины соотношений между элементами реальных волн весьма разнообразны. Поэтому при изучении элементов отдельной волны и их изменения часто используется идеализированная волна, в качестве которой выбирается трохоидальная. Это двумерная волна, частицы которой вращаются по правильным окружностям. При этом частицы, находящиеся на одной вертикали, колеблются синфазно.

Трохоидальный профиль волны заданной высоты и длины можно построить следующим образом. Если окружность радиусом R (рис. 6) катить по горизонтальной прямой (AB), то конец радиуса описывает циклоиду, а остальные точки радиуса описывают трохоиды, соответствующие орбитам с радиусами r = h/2. Волна полной длины образуется после целого оборота катящейся окружности. Принято окружность радиусом R называть катящимся кругом, а радиусом r - производящим кругом.

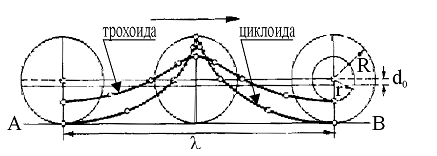
Рис.21. Трохоида и циклоида

Параметры трохоидальной волны определяются из следующих соотношений: лина трохоидальной волны λ равна длине катящегося круга

λ = 2 π R

фазовая скорость трохоидальной волны определяется ее длиной

C_f= =

периода волны

τ=

угловая скорость волны

ω=

С глубиной волнение быстро затухает. Радиусы окружностей, по которым двигаются частицы воды, с увеличением глубины уменьшаются. Тем самым уменьшаются амплитуды колебаний, а, следовательно, и высота волн.

На рис.22 показаны профили волн на поверхности и одновременно на различной

глубине. Из этого рисунка следует:

Рис. 22. Изменение профиля трохоидальной волны с глубиной