Расчетные параметры космических систем, полученных на основе вращающихся гравитационных полей в Космосе.
Вращение – особая форма движения материи
1.
При прямолинейном равномерном движении тела отсутствует ускорение [ 5]. При равномерном вращении тела вокруг своей оси, в нем возникают центробежные или центростремительные ускорения, природу которых современная теория не может объяснить.Согласно существующей теории вращения, вектор угловой скорости и углового ускорения вращающегося тела направлены вдоль оси вращения. Но, по второму закону Ньютона, вектор скорости и ускорения должен совпадать по направлению с вектором силы. В этом случае при ускоренном вращении тело должно не увеличивать скорость вращения, а перемещаться вдоль оси с угловым ускорением. Использование векторного произведения при определении момента силы и момента импульса привело к псевдовекторам, которые не позволили физикам правильно определить направление сил, возникающих при вращении тела. Это и привело к ошибкам в изучении мира Космоса и мира Атома, а также в самой теории вращения.
Момент силы
Согласно современной теории вращения [4], момент силы относительно точки - векторная величина М= [r F], модуль которой равен произведению модуля силы на проекцию l радиуса-вектора r, проведенного из точки О в точку приложения силы F,на направление, перпендикулярное направлению этой силы: М = F·r·sinβ, где β – угол между векторами r и F(Рис.1).
B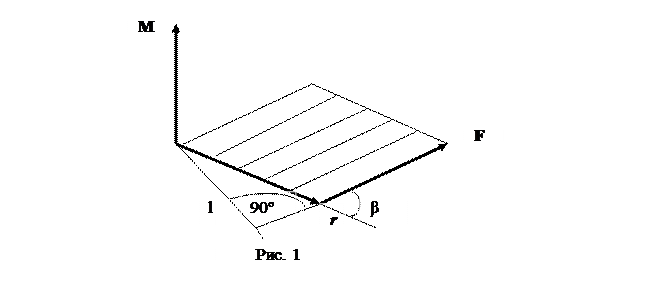 
Но вектор М не отражает реального направления момента силы, так как он является псевдовектором.Эту особенность вектора момента силы и момента импульса отметил в своих лекциях Ф.Фейнман [5]. Кроме того, являясь псевдовектором, момент силы не изменяет своего направления с изменением направления вектора силы F(Рис.1).Ошибказаключается в том, что радиус rрассматривается как вектор, хотя он не меняет своего значения от направления и вектором не является. Более правильно считать радиус плечом рычага, на который действует сила F чтобы повернуть радиус R относительно точки О (Рис.2). Точка О является центром, вокруг которого вращается радиус R под действием силы F. Все силы действуют в одной плоскости.
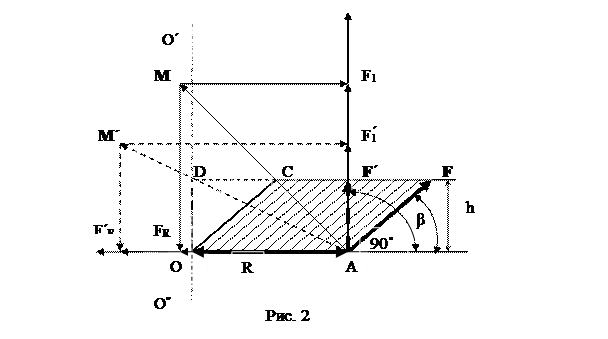
Рассмотрим простейший вариант: на радиус ОА= R исходящей из точки О, действует сила F под углом β, образованным продолжением радиуса и направлением вектора силы F (Рис.2). Модуль момента силы М равен площади параллелограмма OCFA со сторонами R и F. Вектор модуля силы лежит в плоскости параллелограмма и направлен из точки приложения сила А вдоль диагонали.. Вектор момента силы М меняет направление вместе с изменением направления силы F.
Площадь параллелограмма равна произведению основания R на высоту, а высота параллелограмма h = F·sinβ. Таким образом, модуль момента силы М= F·r·sinβ. (Рис.2). Проекция модуля момента силы на радиус дает нам силу AFR действующую на точку А, вдоль радиуса. Проекция модуля М на перпендикуляр к радиусу в точке А дает нам силу AF1, которая и обеспечивает поворот радиуса относительно точки О.
На Рис.2 дан еще один вариант определения момента силы М΄ для силы F΄ действующей на радиус R под углом 90˚.Модуль момента силы М΄ равен площади прямоугольника ODF΄A, который равен площади параллелограмма OCFA. Это означает, что модуль момента силы F равен модулю момента силы .F΄. Но на Рис.2 видно, что направление вектора М΄ изменилось по сравнению с вектором М, что привело к уменьшению силы AF΄ по сравнению с AF. При этом уменьшение F1F1΄ точно равно силе F.Таким образом, сумма сил, действующих вдоль перпендикуляра к радиусу F΄+АF΄ = АF . Если модули векторов сил равны, то это означает, что на радиус R действуют одинаковые силы и данная система должна начать вращаться с одинаковой скоростью.
Проекция модуля момента силы на радиус указывает нам, что в момент начала вращения тела в нем возникают центростремительные силы, направленные вдоль радиуса к центру вращения. В принципе, это доказательство существования во вращательном движении центростремительного ускорения.
Момент сил относительно оси равен моменту сил относительно точки, т.к. ось должна проходить через неподвижную точку О перпендикулярно плоскости разложения сил, а саму ось можно представить как набор точек. Пересечение осью О΄О˝ плоскости разложения сил дает нам точку О, относительно которой и определен момент силы, представленный на Рис.2.
Момент количества движения (импульса)
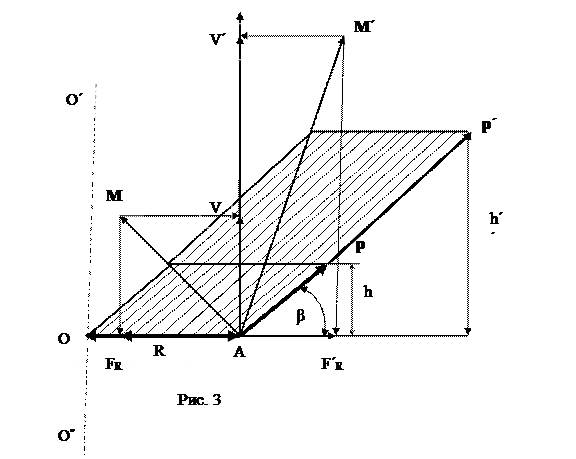
Учитывая, что радиус не вектор, мы получаем на Рис.3 аналогичную картину как на Рис.2. Различие между моментом силы и моментом импульса состоит в том, что сам импульс является произведением скаляра (массы) на вектор (скорость). На Рис.3 видно, что начиная с определенной скорости, проекция модуля импульса на радиус меняет направление, т.е. появятся центробежные силы. Более наглядно этот процесс представлен на графике изменения скорости и ускорения при равноускоренном вращательном движении(Рис.4). Так как все силы действуют в одной плоскости, то момент импульса относительно оси равен моменту импульса относительно точки. Ось проходит через точку О перпендикулярно плоскости разложения сил (Рис.3).
На Рис.3 даны два варианта разложения сил: для импульса р и р΄, действую-
щих на радиус под углом β. Проекция момента импульса Мнарадиус R дает нам центростремительную силу AFR, направленную вдоль радиуса к точке О или оси О΄О˝. А проекция момента импульса М΄ на радиус R дает нам центро-
бежную силу AF΄R , направленную вдоль продолжения радиуса от точки А.
Таким образом, анализ момента сил относительно точки и оси позволил объяснить природу центростремительных сил, возникающих при вращении тела. А определение момента импульса позволило показать, что при вращении тела, в зависимости от скорости, в нем возникают как центростремительные, так и центробежные силы. При этом все силы находятся п одной плоскости, перпендикулярной к оси вращения.
Линейные и угловые скорости и ускорения
Само понятие угловая скорость требует уточнения, как и понятие радиан. Под радианом понимается плоский угол, заключенный между радиусами окружности, длина дуги которой равна радиусу. Более правильно за радиан принимать не плоский угол, а саму дугу окружности, равную по длине радиусу окружности. В этом случае угловая скорость, измеряемая в рад/с, означала бы расстояние в радианах, которое точка, расположенная на поверхности тела, прошла по окружности за определенное время. Такой подход к угловой скорости позволяет однозначно решить проблему направления вектора угловой скорости и углового ускорения.
На Рис.4 дан «График изменения скорости и ускорения при равноускоренном вращательном движении». График построен на основании расчетов скоростей и ускорений для диска с радиусом 10м, который вращается с постоянным угловым ускорением 0,25 рад/с2, начиная с нулевой скорости. График в оригинале выполнен в масштабе 1:100, что позволило наглядно сравнить действующие скорости и ускорения между собой.
В расчетах применялись следующие формулы [4]:
g(aцб) = v2/R (2)
где g – центростремительное ускорение [м/с2];
aцб– центробежное ускорение [м/с2];
v – линейная скорость вращения [м/с];
R – радиус окружности [м].
ал = βR (3)
где ал– линейное ускорение [м/с2];
β – угловое ускорение [рад/с2];
R – радиус окружности /тела/ [м].
ωt = ωo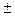 
β t (4)
где ωt – угловая скорость в момент времени t [рад/с];
ωo –угловая скорость в момент времени t = 0 [рад/с];
β – угловое ускорение [рад/с2];
t –время вращения [с].
ωs = ω0·t±β t2/2 (5)
где ωs - путь, пройденный вдоль окружности /угловая координата/, за время t [рад];
ω0 – угловая скорость в момент времени t = 0 [рад/с];
β – угловое ускорение [рад/с2];
t – время движения [с].
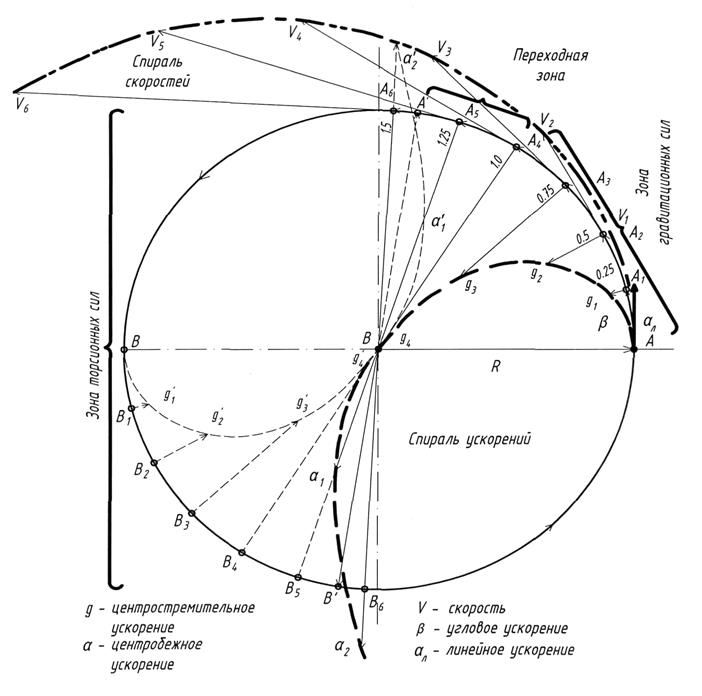
Рис.4
График изменения скорости и ускорения при равноускоренном
вращательном движении.
Согласно условию задачи, вращение тела началось с нулевой скорости, т.е. vo=0 и ωo=0 и с постоянным угловым ускорением равным 0,25 рад/с2.
В этом случае , согласно формуле (3), линейное ускорение ал = 0,25·10 =2,5 м/с2. Но угловое ускорение 0,25 рад/с2 для радиуса R =10м по окружности дает также величину 2,5 м/с2, т.к. дуга АА1 равна 2,5 м. Таким образом получаем, что модуль линейного ускорения равен вектору углового ускорения и лежит с ним в одной плоскости. Кроме того, вектор линейного ускорения направлен вдоль дуги окружности и начинается в точке А как и вектор линейной скорости.
При равноускоренном движении по окружности радиусом R, угловая скорость изменяется по формуле (4). Учитывая, что ωо = 0, а β = 0,25 рад/с2, через 4с угловая скорость в точке А4 = 0,25·4 = 1,0 рад/с, а линейная скорость, согласно формуле (3) будет равна ал = 1·10 =10 м/с (Рис.4). При этом длина дуги А1А2 А3А4 равна 10 м, т.е. модулю линейной скорости, а вектор угловой и линейной скоростей находятся в одной плоскости. Вектор угловой скорости, как и вектор углового ускорения, направлен вдоль дуги окружности. За 6с вращения в режиме равноускоренного движения, точка А пройдет по окружности, согласно формуле (5), расстояние равное 4,5 рад, т.е. повернется на угол 257,8˚.
Центростремительные и центробежные ускорения
Кроме графиков угловых и линейных скоростей и ускорений, на Рис.4 показано изменение нормальных ускорений g и а . Эти ускорения появляются под действием центростремительных или центробежных сил, возникающих при вращении тела. Причины возникновение этих сил показаны на Рис.3, при объяснении момента импульса. На Рис.4 показаны нормальные ускорения, рассчитанные по формуле (2) через каждую секунду (от 0 до 6с) для угловых скоростей от 0 до 1,5 рад/с. Как видно из графиков, при изменении угловой скорости от 0 рад/с до 1,0 рад/с, происходит увеличение нормального ускорения g направленного к центру вращения. Максимальная величина центростремительного ускорения достигается при угловой скорости 1,0 рад/с. Дальнейшее увеличение скорости приводит к появлению центробежного ускорения (а1,а2), которое начинается от центра вращения и направлено вдоль радиуса (точнее, вдоль продолжения радиуса). Это ускорение при вращении тела с угловой скоростью от 1,0 рад/с до 1,41 рад/с полностью компенсирует центростремительное ускорение в пределах окружности (точка В΄). Точка В является симметричной к точке А, и при вращении в ней возникают симметричные ускорения как центростремительные, так и центробежные. В точках А΄ и В΄ происходит полная компенсация центростремительного ускорения. При дальнейшем увеличении скорости вращения за пределами тела действуют только центробежные ускорения. Подтверждением этого является изменение направления сил при увеличении импульса, представленные на Рис.3. При этом, как это видно на Рис.4, в точке А6 действует центробежное ускорение точки В6, а в точке В6 – центробежное ускорение точки А6.
Графики ускорений, представленные на Рис.4 позволяют наглядно оценить особенности предлагаемой теории вращения в познании законов Природы. В Космосе, где угловые скорости вращения составляют тысячные и миллионные доли рад/с, действуют только центростремительные ускорения, как для вещества, так и для гравитационного поля. Они, как правило, связаны с огромными расстояниями и касаются планет, звезд, галактик и Вселенной. Границей перехода центростремительных ускорений в центробежные является угловая скорость в 1 рад/с , которой соответствует 1 оборот за 6,3 с. . Особенностью вращательного движения с угловой скоростью 1 рад/с является равенство линейной скорости и центростремительного ускорения радиусу объекта.
Угловые скорости свыше 1 рад/с широко применяются в производстве и ограничиваются прочностью материала, позволяющего выдерживать огромные центробежные силы.
Этим законам вращения подчиняется как вещество, так и поле, независимо от размера радиуса. В мире Космоса мы имеем дело с веществом и полем. Расчеты, сделанные по формуле (2) показали, что в Космосе гравитационные поля вращаются с угловыми скоростями, составляющими тысячные и даже миллиардные доли рад/с. Сами космические тела вращаются в несколько раз медленнее гравитационных полей. Гравитационное поле Солнца, например, вращается со скоростью 6,277·10-4 рад/с, а само Солнце в 218 раз медленнее. Это означает, что в Космосе мы имеем дело только с центростремительными силами, которые и являются причиной Всемирного притяжения.
В мире Атома мы имеем дело только с полями. Например, в атоме водорода электрон вращается вокруг протона с угловой скоростью 4,13414·1016 рад/с. Это означает, что в атоме действуют только центробежные ускорения, которые и являются теми торсионными полями мира Атома, о которых писал А.Акимов [6]. В связи с этим, учитывая всеобщность законов вращения для мира Атома и мира Космоса, предлагается все центробежные ускорения относить к торсионным силам, а центростремительные ускорения – к гравитационным силам (Рис,4).
При равноускоренном вращательном движении изменение вектора линейной скорости и вектора нормальных ускорений ( центростремительного и центробежного) происходит точно по закону спирали Архимеда. Это говорит о том, что спираль Архимеда является тем математическим аппаратом, который правильно отражает вращательное движение. В спирали Архимеда линейная и угловая скорости располагаются в одной плоскости.
Подводя итог по вращательному движению, можно сделать следующие выводы:
1) Вращение – особая форма движения материи, которая создает в зависимости от скорости вращения, центростремительные или центробежные ускорения. Законы вращения одинаково работают как для вещества, так и для поля.
2) Переход центростремительных ускорений в центробежные происходит при угловой скорости вращения в 1 рад/с. При такой угловой скорости вращения тела его линейная скорость и центростремительное ускорение равны радиусу тела.
3) При вращении направления всех скоростей и ускорений находятся в одной плоскости. Вектор угловой скорости и ускорения направлен вдоль окружности и по модулю равен линейной скорости и ускорению.
4) Торсионные и гравитационные поля, имея одинаковую природу –вращение материи, различаются только направлением возникающих сил и скоростью вращения. Поэтому космические формулы должны работать и в мире Атома.
3. Гравитационные поля в космических системах
Под космической системой понимается часть Космоса, включающая в себя центральный космический объект и связанные с ним тела, вращающиеся вокруг него. Такими системами являются: планета со своими спутниками, Солнечная система, Галактика с ядром, диском и гало. Особое место в системах занимает сама Вселенная.
Открытие вращающихся гравитационных полей в космических объектах и раскрытие природы гравитационной постоянной G, позволили определить связь ядра нашей Галактики со всеми космическими объектами в ней. Ядро Галактики имеет свое вращающееся гравитационное поле, угловая скорость которого ω = 6,672х10-11 с-1. На Земле она измеряется в м3/кг с2 и является гравитационной постоянной G для Солнечной системы и всей нашей Галактики. Гравитационное поле ядра Галактики распространяется и вращается со скоростью 2,9979х108 м/с, т.е. со скоростью света. Таким образом, гравитационная постоянная G и скорость света с – параметры вращающихся гравитационных полей ядра нашей Галактики. Гравитационный потенциал Галактики равен квадрату скорости света Uг = 8,9874·1016 м2/с2 .
Вращающееся гравитационное поле ядра Галактики наводит во всех объектах Галактики собственные вращающиеся гравитационные поля. Угловая скорость вращения наведенных полей, например, в нашей Солнечной системе составляет от тысячных до десятитысячных долей радиан в секунду. Сами космические объекты вращаются в несколько раз медленнее своих гравитационных полей. Наше Солнце вращается медленнее своего поля в 218 раз, а Юпитер - в 3,5 раза. Это означает, что в Космосе постоянно действуют только центростремительные ускорения, которые и являются причиной Всемирного притяжения
Наведенная угловая скорость поля зависит от плотности космического объекта и определяется по формуле:
G΄2 =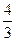 
π·ρ·G (6)
где G' – гравитационная постоянная космического объекта (угловая скорость вращения его гравитационного поля) [с-1];
ρ – плотность космического объекта [кг/м3];
G – гравитационная постоянная, равная 6,672·10-11 [м3/кг с2].
Линейная скорость вращения наведенного гравитационного поля является первой космической скоростью для данного объекта, а угловая скорость вращения численно равна частоте данной волны[2,3].
Гравитационные поля обладают собственной гравитационной массой, которая зависит только от скорости вращения и радиуса. Эта гравитационная масса М´ определяется по формуле:
М΄ = V΄·R2 = ω·R3 (7)
Где М΄ -гравитационная масса [кг=м3/с];
V΄ - линейная скорость поля [м/с];
R – радиус космического объекта [м];
ω – угловая скорость вращения [рад/с = с-1]
Примечание. 1)Угловая скорость наведенного гравитационного поля космического объекта является гравитационной постоянной данного объекта, т.е. ω = G´, поэтому в формуле (7) можно вместо ω·R3 записать G´·R3.
2) Гравитационная масса, согласно формуле (7), должна измеряться в м3/с а не в кг. Изучение гравитации показало, что эти единицы эквивалентны, т.е. м3/с=кг и в основном зависят от единиц измерения гравитационной постоянной.
Внутри космического тела гравитационная масса составляет, как правило, миллионные доли массы вещества. Но именно эта гравитационная масса и создает основную часть гравитации космического объекта.
. В космических системах, таких как Солнечная, Галактическая и самой Вселенной соотношение масс гравитационного поля и вещества противоположное.
Наша Солнечная система состоит из двух систем, наложенных друг на друга. Во-первых, это космическая система, центром которой является Солнце, а во-вторых, система Солнце – Юпитер, центр которой расположен за пределами радиуса Солнца. Граница солнечной системы определяется гравитационным полем системы Солнце – Юпитер.
Гравитационная волна космического объекта, выйдя за пределы объекта, распространяется со скоростью света, а ее длина, которая в пределах космического объекта равнялась радиусу объекта, изменяется согласно формуле:
λ = с/ν (8)
где λ – длина волны [м];
с – скорость света [м/с];
ν – частота волны [с-1].
На примере Солнца имеем: при частоте гравитационной волны 6,277·10-4 с-1 длина волны за пределами Солнца равняется 4,776·1011 м. Эта длина волны соответствует расстоянию от Солнца до пояса астероидов. При этом наблюдается определенная зависимость между кратностью длин волн и орбитами планет. Орбиты, пояса Койпера, пояса Оорта , возможно связаны с длинами гравитационных волн соседних планет. Более того, можно сказать, что за пояс астероидов отвечает Солнце, за пояс Койпера - Юпитер и Сатурн, а за облако Орта – система Солнце - Юпитер. Если считать, что облако Орта - это конец Солнечной системы, то ее радиус составляет не менее 7,1·1012м.
Подобно Солнцу, все планеты солнечной системы обладают своими гравитационными полями. При этом, как видно на Рис.6, длина внешней гравитационной волны у таких планет как Юпитер, Сатурн, Уран и Нептун больше чем у Солнца. Орбиты планет Солнечной системы, в основном, располагаются в пределах длины волны, Исключение составляют Сатурн и Уран, орбиты которых приходится на участок между длинами волн (Рис.6).
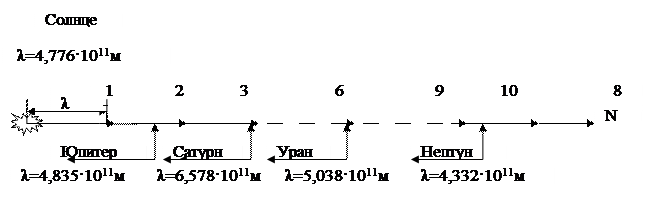
Рис.6
Схема расположения некоторых планет Солнечной системы вдоль распространения сферических волн Солнца с указанием их собственных длин гравитационных волн. (N – число длин гравитационной волны Солнца).
Наложение гравитационных волн планет Солнечной системы периодически ослабляет гравитацию на Солнце, что и приводит к увеличению солнечной активности в виде протуберанцев и солнечных пятен. При этом за 11-летний цикл отвечает, скорее всего, Юпитер и Сатурн, а за 200-летний цикл – Уран и Нептун.
Теория вращающихся гравитационных полей позволяет по иному взглянуть на спирали нашей Галактики. Форма спиралей отражает скорости вращения гравитационного поля в системе Галактики. На репродукции (Рис.7) представлены спирали нашей Галактики, построенные на основании радио и оптических наблюдений. На репродукции видно, что все спирали пересекают радиус под одним и тем же углом. Для нашей Галактики он равен 80˚. Эти условия соответствуют логарифмической спирали. На схеме Главной спирали нашей Галактики (Рис.8), выполненной на оригинале в масштабе 1см = 0,2 кПк, видно, что в центре спирали находится ядро Галактики с радиусом 4,492·1018 м или 475 световых лет. Наше Солнце располагается на четвертом витке спирали от ядра Галактики. Учитывая, что в нашей Галактике 4 спирали, то балдж, обозначенный на схеме пунктирным кругом, захватывая третий виток, представляет собой наложение 12 витков спиралей, что не позволяет различать сами спирали. Поэтому на репродукции (Рис.7) за балджем информация отсутствует.
Рис.7
Вращающееся гравитационное поле нашей Галактики, из-за огромной массы, изменяет свою скорость вращения от центра к периферии. Скорость вращения гравитационных масс полей V'' в системах рассчитывается по формуле:
V"3 = М´2·G'/R˝3 (9)
где V"- линейная скорость гравитационной массы системы [ м/с ];
М΄ - гравитационная масса центрального тела [кг];
G΄- гравитационная постоянная центрального тела [с-1];
R˝ - радиус космической системы [м].
Для орбиты Солнца R˝= 2,57·1020 м, а для ядра Галактики М´= 6,048·1045 кг, G´= 6,672·10-11 с-1. Скорость вращения гравитационной массы поля Галактики на орбите Солнца V"= 5,239·106 м/с. Учитывая стабильное положение спиралей в Галактике, можно предположить, что спирали Галактики вращаются со скоростью гравитационного поля системы. При этом соблюдается равенство:
V´г·Rг = V˝· R˝ (10)
Где V´ г - линейная скорость вращения поля ядра Галактики [м/с]:
V˝ – линейная скорость вращения поля системы [м/с];
R˝ - радиус системы [м];
Rг – радиус ядра Галактики [м].
Если равенства (9) применить для Солнечной системы на орбите Земли, то получим скорость вращения гравитационного поля системы V"= 2,0318х103 м/с. Гравитационное поле самого Солнца вращается со скоростью 4,3681·105м/с. Среднегеометрическая величина скорости вращения гравитационного поля самого Солнца и скорости вращения гравитационного поля системы Солнце - Земля дает нам орбитальную скорость Земли вокруг Солнца: Vорб =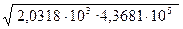 
= 2,979х104м/с. Среднегеометрическая зависимость орбитальных скоростей соблюдается для всех планет солнечной системы. Даже в системе Земля – Луна, скорость вращения Луны строго подчиняется этой закономерности. Это означает, что скорость вращения всех планет Солнечной системы напрямую связана со скоростью вращения гравитационного поля Солнца и не зависит от массы планет. Другими словами, гравитационное поле Солнца вращает все планеты Солнечной системы. Аналогично, гравитационные поля планет вращают свои спутники.
Гравитационные поля космических объектов и вращение гравитационных полей космических систем позволяют разгадать некоторые загадки космической навигации. В научно-популярной литературе [7] появилась информация, что космические аппараты NASA Пионер-10 и Пионер-11 за орбитой Юпитера и Сатурна уменьшают скорость почти в два раза, а на границе Солнечной системы отклонились от расчетных орбит до 400000км. Главной причиной снижения скорости является неправильное определение ускорения на поверхности Юпитера и Сатурна. Расчет ускорения по формуле g = MG/R2 дает величину ускорения равную 25,24 м/с2. Это ускорение создается только за счет вращения гравитационного поля Юпитера. Если учитывать ускорение, которое создается вращением самого Юпитера, то необходимо добавить еще g = V2/R = 125662/7,085·107 = 2,23м/с2, Таким образом, суммарное ускорение на Юпитере составляет27,47 м/с2, которое и влияет на скорость аппаратов. Аналогичная картина наблюдается и для Сатурна. При расчетном ускорении 10,53 и/с2, фактическое ускорение составляет 12,29 м/с2. Причиной отклонения орбит аппаратов на 400000 км является вращение гравитационного поля солнечной системы, которое сносит аппараты с расчетных орбит. Кроме того, за Юпитером действуют гравитационные законы системы Солнце – Юпитер.
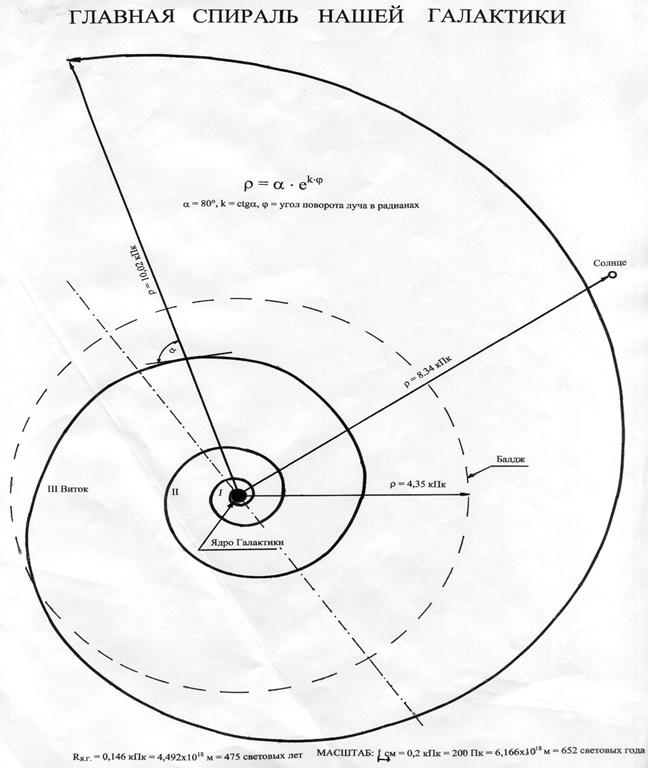
Рис.8
4. .Арифметика Космоса
Открытие вращающихся гравитационных полей в Космосе и гравитационной массы
позволили рассчитать дополнительные параметры для Солнца, Солнечной системы, ядра Галактики, системы Галактика и даже варианта Вселенной. Эти данные представлены в Таблице1, а формулы, по которым производились расчеты, представлены ниже.
В в графе масса вещества для Солнечной и Галактической систем дается условная масса вещества системы, которая, в отличии от массы Солнца и массы ядра Галактики, определялась по формуле (11). Условная масса вещества системы - максимальная масса вещества, которую может удержать центральное тело системы за счет сил гравитации без учета массы самого центрального тела. Для расчета массы вещества системы применялась эмпирическая формула:
Мсис = М'· g2 (11) определенная связь
где Мсис –условная масса вещества системы [кг];
М' – масса гравитационного поля центрального тела [кг];
g - центростремительное ускорение [ м/с2 ];
Формула (11) была получена по результатам анализа распределения масс планет и и масс спутников планет Солнечной системы с применением теории вращающихся гравитационных полей. Проверка показала, что Солнечная система и сами планеты подчиняются этой формуле. Исключение составили системы Земля – Луна и Плутон – Харон. Масса Луны, равная 7,35·1022 кг, оказалась в 2380 раз больше условной массы, равной 3,0886·1019 кг, которую может удержать гравитационное поле Земли. Возможно, этим объясняется постоянное удаление Луны от Земли.
Применение формулы (11) для нашей Галактики дало значение условной массы вещества галактической системы равное 2,422·1042 кг. В данной массе вещества системы Галактика не учитывается масса вещества ядра Галактики, которая составляет 1,822·1053кг. Но не эта масса является движущей силой Галактики, а вращающиеся гравитационное поле ядра Галактики, масса которого составляет 6,048·1045 кг, т.е. одну тридцати миллионную долю массы вещества ядра Галактики.
Как видно из Таблицы 1, в системе Галактика масса гравитационного поля достигает 6,793·1055 кг, что в 373 раза больше массы вещества ядра галактики равной 1,822·1053кг. Условная масса вещества (звезд и планет), равная 2,422·1042 кг, практически не влияет на суммарную гравитацио массу Галактики.
Масса гравитационных полей космических систем и является той «темной материей», которую уже не одно десятилетие пытаются безуспешно найти ученые всего мира. Эта масса появляется при вращении гравитационного поля, как в космических объектах, так и в космических системах. В Таблице 1 масса гравитационного поля Солнца, Солнечной системы, ядра Галактики, Галактической системы и Вселенной - это «темная материя» Космоса.
Таблица 1
Расчетные параметры космических систем, полученных на основе вращающихся гравитационных полей в Космосе.
| № | Параметры | Солнце | Солнечная система | Ядро Галактики | Галакти- ческая система | Вселенная |
| Радиус, R (м) В ско Радиус, R ( Пк ) | 6,96·108 (2,258·10-8) | 3,278·1014 (1,063·10-2) | 4,492·1018 (1,457·102) | 1,006·1022 (3,263·105) | 3,031·1029 (9,831·1012) | |
| Масса вещества, М (кг) | 1,99·1030 | 1,592·1028 | 1,822·1053 | 2,422·1042 | 2,048·1063 | |
| Масса гравитационного поля, M΄ (м3/с) | 2,116·1023 | 2,211·1040 | 6,048·1045 | 6,793·1055 | 6,171·1070 | |
| Плотность вещества, ρ (кг/м3) | 1,409·103 | 1,079·10-16 | 4,799·10-4 | 5,679·10-25 | 1,226·10-30 | |
| Плотность гравитационного поля, ρ (с-1) | 1,499·10-4 | 6,7553·10-16 | 1,593·10-11 | 3,1756·10-18 | 5,530·10-19 | |
| Гравитационный потенциал, U (м2/с2) | 1,908·1011 | 4,0503·105 | 8,988·1016 | 4,0112·1013 | 4,511·1023 | |
| Скорость гравитационной волны V΄ (м/с) | 4,369·105 | 2,988·108 | 2,988·108 | 2,988·108 | 6,717·1011 | |
| Круговая скорость вращения гравитационного поля, V''(м/с) | 4,369·105 | 0,9273 | 2,998·108 | 1,3383·105 | 6,717·1011 | |
| Гравитационная постоянная (угловая скорость вращения гравитационного поля), G΄(с-1) | 6,277·10-4 | 6,277·10-4 | 6,672·10-11 | 6,672·10-11 | 2,216·10-18 | |
| Центростремительное ускорение, g (м/с2) | 274,17 | 3,0497·10-9 | 2,001·10-2 | 3,986·10-9 | 1,488·10-6 | |
| Объем ύ (м3) | 1,412·1027 | 1,475·1044 | 3,797·1056 | 4,265·1066 | 1,116·1089 |
Примечание: 1. Массы вещества и поля эквивалентны между собой.
2. Плотности вещества и поля эквивалентны между собой.
3. В системах массы даны без массы центральных тел.
Открытие вращающихся гравитационных полей показало, что в Галактике существует четкая связь между ядром Галактики и окружающими ее космическими объектами. Для оценки связи планет Солнечной системы с ядром Галактики вначале были рассчитаны коэффициент потенциала Кu и коэффициент гравитации Кg :
Кu = Uг /Uпл (12)
Kg = Gг /Gпл (13)
где Uг – гравитационный потенциал Галактики [м2/с2];
Uпл – гравитационный потенциал планеты [м2/с2];
Gг – гравитационная постоянная Галактики [м3/кг·с2=с-1];
Gпл – гравитационная постоянная планеты [с-1];
. Для Солнца Кu= 4,71х105 , а Кg = 1,0634х10-7 .Эти коэффициенты, определенные для Солнца и всех планет Солнечной системы стали отправной точкой для поиска новых закономерностей и констант в Космосе. Коэффициенты позволяют по массе вещества определить его гравитационную массу, а по радиусу планеты определить длину ее гравитационной волны за пределами планеты:
М΄ = М· Кg (14)
λвн= Rпл ·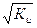 
(15)
где М' – гравитационная масса объекта [кг];
Кg – гравитационный коэффициент космического объекта;
λ – длина внешней гравитационной волны [м];
Rпл – радиус планеты [м]
Ku – коэффициент потенциала космического объекта.
На примере Солнца имеем: масса вещества Солнца М = 1,99·1030 кг., а гравитационная масса М΄=1,99·1030 ·1,0634х10-7 = 2,116·1023 кг. Кроме того, применение коэффициентов позволяет упростить формулы.
В процессе изучения Космоса одной из первых была получена приведенная гравитационная постоянная нашей Галактики:
Constг = 1 / (4/3π·G) = 3,578·109 кг·с2/м3 (16)
Где Constг – приведенная гравитационная постоянная [кг·с2/м3];
G – гравитационная постоянная [м3/кг·с2].
Эта приведенная постоянная позволяет установить связь между плотностью, ускорением и радиусом космического объекта:
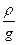·R = 3,578·109 кг·с2/м3 (17)
Где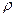 
- плотность космического объекта [кг/м3];
g – ускорение космического объекта [м/с2 ];
R – радиус космического объекта [м ] ;
3,587·109- Сonstг [кг·с2/м3].
Данная формула справедлива для всей нашей Галактики и позволяет по любым из двух параметров космического объекта определить третий параметр. Если в этой формуле заменим Constг на приведенную постоянную Вселенной Constвс = 1,0773·1017 кг·с2/м3 , то, зная R и g (Таблица1), сможем определить плотность вещества ядра нашей Галактики:
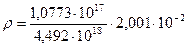= 4,799·10-4 кг/м3.
Формула (17) позволяет заглянуть в механизм создания звезд и планет. При условии, когда плотность космического объекта равна его ускорению, радиус планеты должен равняться приведенной постоянной Const, т.е. 3,578·109 м. Если плотность меньше ускорения, радиус космического объекта будет больше Constг, например звезды гиганты. Если плотность больше ускорения, то радиус космического объекта меньше 3,578·109 м, что мы и наблюдаем в нашей Солнечной системе и для большинства звезд нашей Галактики.
Формула (17) позволяет определить плотность идеального белого карлика, у которого гравитационное поле вращается с угловой скоростью 1 рад/с. Согласно ,предлагаемой теории вращения, при скорости в 1 рад/с ускорение космического объекта численно равно радиусу объекта. Из формулы (17) следует, если R=g, то плотность ρ должна равняться приведенной постоянной, т.е. 3,578·109 кг/м3.
Такое же значение плотности можно получить, применяя формулу (6). В этой формуле G´=ω, и при условии, что ω = 1 рад/с, получим:
ρ =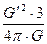 
= 
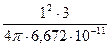= 3,578·109 кг/м3.
Примером идеального белого карлика является Сириус В. По данным в учебнике В.С.Бескина «Гравитация и астрофизика» (с.80, Таблица1), масса Сириуса В составляет 1,05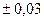 
массы Солнца, а радиус 0,0074 
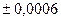радиуса Солнца. По массе М = 2,09·1030кг и радиусу R = 5,15·106м через объем можно рассчитать плотность Сириуса В:·
ρ =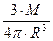 
= 
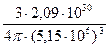= 3,65·109 кг/м3. (18)
Далее, по формуле (1) можно определить гравитационный потенциал Сириуса В U = 2,09·1030· 6,672·10-11 / 5,15·106 = 2,71·1013 м2/с2. По гравитационному потенциалу и радиусу можно определить ускорение на Сириус В g = U/R = 2,71·1013 / 5,15·106 = 5,26·106 м/с2. Линейная скорость вращения гравитационного поля V =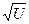 
= 
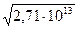= 5,21·106 м/с2. Учитывая погрешность при определении массы и радиуса Сириуса В, можно считать, что радиус, линейная скорость и ускорение на Сириусе В равны между собой. Но согласно новой теории вращения, это возможно только при условии, что угловая скорость равна 1 рад/с.
Угловую скорость вращения гравитационного поля Сириуса В можно определить по формуле (6):
G´ =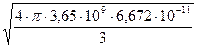 
= 1,01 с-1.
Таким образом, Сириус В является представителем идеального белого карлика. Более того, плотность белого карлика практически равна приведенной гравитационной постоянной согласно формуле (17). Отсюда можно сделать вывод, что скорость вращения вещества идеальных белых карликов равна скорости вращения его гравитационного поля!
Остальные белые карлики (40 Эридана В, CD-38 10980, Wolf 485А и др.), представленные в Таблице 1 являются рядовыми белыми карликами, у них угловая скорость вращения гравитационного поля менее 1 рад/с.
В Космосе угловые скорости вращения более 1 рад/с могут быть у нейтронных звезд. Но в этом случае вращаются не гравитационные, а торсионные поля и действуют центробежные силы.
В формулах (17) и (6) под плотностью космического объекта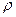 
понимается его средняя плотность в кг/м3. Обычно она определяется делением массы объекта на его объем. Но каким образом эту плотность объектов определяет сама природа? Например, у Солнца она изменяется от космического вакуума до плотности атома, но средняя считается 1409 кг/м3. В предыдущей главе упоминается, что в Космосе часто работает закон среднегеометрической величины. Так не является ли средняя плотность среднегеометрической величиной для максимальной и минимальной плотности космического объекта? Если принять максимальную плотность Солнца 1016 кг/м3, а среднегеометрическую 1409 кг/м3, то минимальная плотность Солнца должна быть:
= 
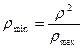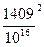= 1,985·10-11 кг/м3. (19)
Эта величина плотности вполне соответствует космическому вакууму.
На примере нашей Земли, принимая за минимальную плотность земной коры 2,2·103 кг/м3, а за среднюю 5,533·103 кг/м3 можем определить плотность в центре Земли:
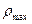=(5,533·103)2/2,2·103 = 13,92·103 кг/м3.
Эта максимальная плотность в центре Земли вполне согласуется с научными данными плотности на глубине 5·106м равными 11,5·103кг/м3 [4], при радиусе Земли 6,378·106м.
Эта максимальная плотность в центре Земли вполне согласуется с научными данными плотности на глубине 5·106м равными 11,5·103кг/м3 [4], при радиусе Земли 6,378·106м.
Поиск новых закономерностей в Космосе привел к космической константе Кк:
Кк =U · G'= V'· g (20)
Где Кк – космическая константа [м2/с3];
U – гравитационный потенциал [м2/с2];
G΄- гравитационная постоянная космического объекта [с-1];
V΄ - линейная скорость гравитационной волны [м/с];
g - центростремительное ускорение [м/с2].
Космическую константу можно рассматривать как гравитационную характеристику космического объекта. В ней не учитывается вещество объекта, а только гравитационное поле, параметры которого взаимосвязаны между собой.
Космическая константа ядра Галактики Кг = 6·106 м2/с3. В Солнечной системе космическая константа Солнца в 20 раз больше константы ядра Галактики, а у Сатурна в 20 раз меньше. Юпитер занимает промежуточное значение, его константа в 5,27 раз меньше ядра Галактики.
Согласно теории вращающихся гравитационных полей Вселенная должна иметь свою космическую константу, т.е. гравитационный потенциал, гравитационную постоянную, линейную скорость и центростремительное ускорение. Для планет Солнечной системы, Солнца и Галактики эти параметры можно рассчитать. Для Вселенной все эти параметры неизвестны. Но анализ Солнечной системы и системы Галактика показал, что несмотря на колоссальные различия в размерах, их вращающиеся гравитационные поля подчинены одним и тем же формулам. В связи с этим, появилась идея использовать коэффициенты Кu и Кg для определения гравитационного потенциала и гравитационной постоянной Вселенной, предполагая, что планеты Солнечной системы относятся к Галактике как ядро Галактики относится к Вселенной. Учитывая, что космическая константа Юпитера меньше всех отличается от космической константы Галактики, Юпитер и был взят для ориентировочной оценки параметров Вселенной по первому варианту. Второй вариант определения параметров Вселенной заключался в том, что отправной точкой служила не Солнечная система, а параметры самой Галактики. При расчетах применялись формулы проверенные в системе Солнце – Галактика:
21) 
= 
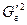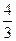π·ρ·Gвс ; 22) U вс= 
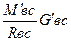; 23) Квс = Uвс·Gвс = V'вс· 
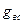; 24)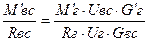 
.; 25) V'вс = 
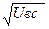;. 26) Rвс= 
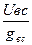; . 27) Мвс =М΄вс·Кg галл.
Для Вселенной, в принципе, нельзя получить коэффициенты Кu и Кg , т.к. она - последняя инстанция в системе управления Космосом. Вселенная сочетает в себе свойства космического объекта и космической системы. Поэтому для определения массы вещества Вселенной было взят коэффициент Кg ядра Галактики. Учитывая, что Вселенная – система и ее масса поля должна быть больше массы вещества, этот коэффициент умножался на гравитационную массу поля Вселенной согласно формуле (27).
Из двух вариантов расчета параметров Вселенной за основу был взят второй /по Галактике/, т.к. по нему гравитационная постоянная Вселенной практически равна постоянной Хаббла. Космическая постоянная Вселенной Квс = 1·106 м2/с3. По первому варианту гравитационная постоянная получалась больше в 3,2 раза, а радиус Вселенной меньше в 6,8 раза, чем по второму варианту. Параметры Вселенной по второму варианту представлены в Таблице 1. Расчетные параметры Вселенной могут различаться с параметрами истиной Вселенной, но учитывая, что два метода расчетов дали практически сопоставимые результаты, то данные параметры Вселенной можно принять за основу для дальнейшего изучения Космоса.
В качестве доказательства реальности рассчитанных параметров Вселенной можно привести четыре фактора:
Во-первых, гравитационная постоянная Вселенной G'вс = 2,216х10-18 с-1 – это постоянная Хаббла, которая находит практическое подтверждение при изучении дальнего Космоса.
Во-вторых, обратная величина гравитационной постоянной дает нам время прохождения гравитационной волны Вселенной от ее центра до периферии. Оно составляет 13,4 миллиарда лет – время жизни Вселенной принятое на сегодня наукой.
В-третьих, центростремительное ускорение Вселенной ограничивает видимую часть спиралей всех галактик. Видимая главная спираль нашей Галактики кончается на расстоянии 10 кПк, где центростремительное ускорение ядра Галактики падает до 1,43·10-6 м/с2. На этой границе практически кончается преимущественное влияние ядра Галактики на звезды. На их движение начинает влиять гравитационные поля Вселенной и соседних галактик.
В-четвертых, плотность вещества во Вселенной находится в пределах "критических" плотностей, рассчитанных учеными.
Выводы
Подводя итоги всему сказанному о космических системах можно сделать следующие выводы:
1) Предложена новая теория вращательного движения, которая объясняет причину возникновения при вращении центростремительных и центробежных ускорений.
2) Согласно новой теории вращения, векторы угловых скоростей и ускорений и векторы линейных скоростей и ускорений находятся в плоскости вращения. При этом вектор угловой скорости и ускорения направлены вдоль окружности, а модуль угловой скорости равен модулю линейной скорости.
3) Новая теория вращения позволяет связать мир Космоса с миром Атома.
4) Дана формула для определения скорости вращения гравитационного поля, с учетом его гравитационной массы для космических систем.
5) Средняя плотность космического объекта - это среднегеометрическая величина для максимальной и минимальной плотностей данного объекта.
6) Рассчитана форма Главной спирали нашей Галактики и ее скорость вращения на орбите Солнечной системы вокруг центра Галактики.
7) Показано взаимодействие гравитационных полей Юпитера, Сатурна, Урана и Нептуна с гравитационным полем Солнца.
8) В Таблице 1 даны расчетные параметры для Солнечной и Галактической систем, и рассчитаны предполагаемые параметры Вселенной.
Заключение
В заключении я хотел бы остановится на некоторых проблемах современной науки, которые можно объяснить, опираясь на теорию вращающихся гравитационных полей в Космосе:
1) Эта теория позволяет объяснить причину наклона орбит планет в Солнечной системе. Наклон орбит вызван действием сил Кориолиса, которые появляются при взаимодействии вращающихся гравитационных полей планет с вращающимся гравитационным полем Солнца.
2) Появление пятен на Солнце является следствием уменьшения центростремительного ускорения на поверхности Солнца под действием гравитационных полей планет Солнечной системы.
3) Землетрясение в Японии в 2011 году спровоцировала Луна, которая в том году находилась на ближайшей орбите к Земле. Повторные землетрясения связаны с тем, что после удаления Луны от Земли, притяжение гравитационного поля Земли возвращает тектонические плиты на место. Эхом этого процесса служат землетрясения в других отдаленных точках Земли со сложной тектоникой.
4) Формула G'2 =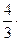 
π·ρ·G дает ответ на то, как в Космосе возникают новые звезды. Ядро Галактики в пылевых облаках создает вращающиеся гравитационные поля, которые и становятся центрами будущих звезд.
5/ Открытие вращающихся гравитационных полей и гравитационной массы в Космосе позволили не только раскрыть секрет Всемирного тяготения, но и через новую теорию вращения связать мир Космоса с миром Атома.
6/ Вращающие гравитационные поля планет и всей солнечной системы позволяют объяснить причины замедления скоростей космических аппаратов и их отклонение от расчетных орбит за орбитой Юпитера и Сатурна.
Я надеюсь, что в будущем теория вращающихся гравитационных полей поможет ученым разгадать еще многие тайны Природы.
| <== предыдущая лекция | | | следующая лекция ==> |
| Современное состояние. Физика атмосферы (нижней части атмосферы) – наука о строении атмосферы, свойствах и протекающих в ней процессах | | | ИЗУЧЕНИЕ ВУЛКАНОГЕННЫХ ОБРАЗОВАНИЙ |
Дата добавления: 2016-02-02; просмотров: 675;