К о с в е н н о е п о д о б и е
Отношениекосвенного подобия(аналогия) устанавливается не в результате физического взаимодействия, а объективно существует в природе и обнаруживается в форме совпадения абстрактных моделей, а затем используется в практике моделирования (например, электромеханические аналогии).
Рассмотрим пример, использующий электромеханическую аналогию.
Пример. Пусть механическая система состоит из пружины с жесткостью k, подвешенного на ней груза массой m и демпфера с коэффициентом вязкости b (рис. 1.4).

Рис.1.4. Механическая система, состоящая из пружины, груза и демпфера
В качестве входной переменной рассматривается вынуждающая сила F(t), а выходной переменной является расстояние до точки подвеса y(t). В этом случае вертикальные колебания груза можно описать уравнением:
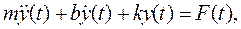
где первое слагаемое в левой части уравнения соответствует второму закону Ньютона для движения тела массой m, второе слагаемое описывает действие демпфера, а третье – пружины.
В общем виде это линейное дифференциальное уравнение 2-го порядка можно записать:
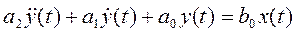 ,
,
где m=a2, b=a1, k=a0, F(t)=x(t).
Теперь рассмотрим электрическую систему, состоящую из источника ЭДС, являющейся внешним воздействием, активного сопротивления R, индуктивности L и емкости С (рис.1.5). Выходной переменной будем считать величину тока i(t).
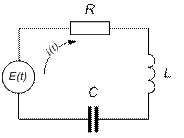
 Рис. 1.5. Электрическая система, состоящая из источника ЭДС, активного сопротивления, индуктивности и емкости
Рис. 1.5. Электрическая система, состоящая из источника ЭДС, активного сопротивления, индуктивности и емкости
Согласно второму закону Ома сумма падений напряжений в цепи равна сумме ЭДС, поэтому уравнение, описывающее изменение тока в этой системе, будет иметь вид:
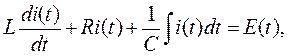
или, если продифференцировать по t и умножить на С обе части уравнения:
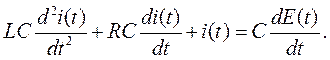
Обозначив LC=a2, RC=a1, 1= a0, C=b0, dE(t)/dt=x(t), получим:
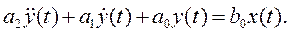
 Таким образом, при описании процесса, протекающего в электрической системе, мы получили линейное дифференциальное уравнение 2-го порядка, абсолютно идентичное тому, которое описывало процесс, протекающий в механической системе. Это и означает, что данные системы косвенно подобны.
Таким образом, при описании процесса, протекающего в электрической системе, мы получили линейное дифференциальное уравнение 2-го порядка, абсолютно идентичное тому, которое описывало процесс, протекающий в механической системе. Это и означает, что данные системы косвенно подобны.
Дата добавления: 2016-02-02; просмотров: 674;
