Переход породы в новое напряжённо - деформированное состояние
В нетронутом массиве породы на глубине H на площадку с нормальным вектором, параллельным вертикальной оси Z, действует эффективное давление, равное разности горного и пластового давлений
Pz = ρп g H – Рпл , (3.1)
где ρп - усреднённая плотность породы, Н – глубина ,g–ускорение свободного падения, Рпл – пластовое давление на глубине Н.
 Боковые давления на площадках, перпендикулярных осям Х и Y, в общем случае могут быть не одинаковыми. При равенстве давления в породе напряжению, можно говорить о том, что на глубине H действует комплекс напряжений:
Боковые давления на площадках, перпендикулярных осям Х и Y, в общем случае могут быть не одинаковыми. При равенстве давления в породе напряжению, можно говорить о том, что на глубине H действует комплекс напряжений: 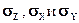 . Для изотропной среды можно допустить
. Для изотропной среды можно допустить 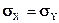 и
и 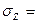 Pz. Понятно, что
Pz. Понятно, что 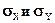 будут составлять только какую–то часть
будут составлять только какую–то часть 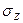 . (рис. №3.1)
. (рис. №3.1)
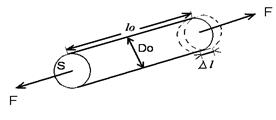
Для оценки боковых напряжений рассмотрим некоторые положения теории упругости. При растяжении цилиндрического твёрдого тела силой F по схеме, представленной на рисунке №3.2, его длина и диаметр претерпят изменения. Относительные деформации длины и диаметра цилиндра обозначим 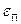 и
и 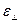 , соответственно.
, соответственно.
 .
.

Относительные деформации, выраженные через геометрические размеры цилиндра равны:
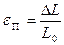 и
и 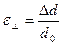 .
. 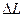 -суммарное удлинение.
-суммарное удлинение.
Поперечное сечение цилиндра – S. Тогда действующее напряжение в твёрдом теле будет равно 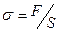 .
.
Отношение относительного уменьшения диаметра цилиндра 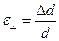 к относительному удлинению цилиндра
к относительному удлинению цилиндра 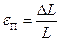 называется коэффициентом Пуассона:
называется коэффициентом Пуассона:
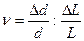 .
.  (3.2)
(3.2)
Естественно, боковые напряжения должны выражаться через коэффициент
Пуассона. Для упрощения решения будем считать породу изотропной средой. Тогда в пределах упругих деформаций можно ввести понятие коэффициента бокового распора:
Тогда в пределах упругих деформаций можно ввести понятие коэффициента бокового распора:
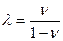 . (3.3)
. (3.3)
Напряжения 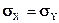 =
= 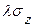 . Таким образом, боковые напряжения в нетронутом массиве выражаются через коэффициент бокового распора и напряжение, создаваемое горным давлением.
. Таким образом, боковые напряжения в нетронутом массиве выражаются через коэффициент бокового распора и напряжение, создаваемое горным давлением.
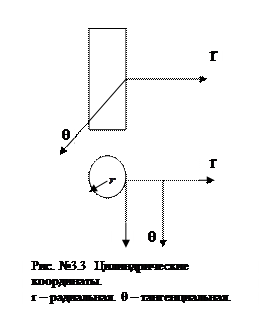
Бурение скважины сопровождается переходом пород в окрестности ствола в новое напряжённо – деформированное состояние. Теперь приведённые соотношения действительны только в достаточно удалённых от скважины зонах. Для скважины необходимо ввести цилиндрические координаты.
Координата r может вращаться относительно оси скважины, вследствие допущения об изотропности породы.
Координата θ, являясь скользящей и может перемещаться вдоль координаты r, оставаясь перпендикулярной r.
Достаточно простые решения могут быть получены для случая отсутствия фильтрации и постоянства скачка давления на стенке скважины равному разности забойного и пластового давления в скважине на глубине залегания пласта. Решение будет распространяться для области
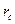 ≤ r ≤ ∞.
≤ r ≤ ∞.
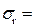
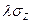
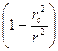 + a
+ a 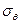 =
= 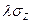
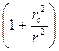 - a; (3.4)
- a; (3.4)
где a  ,
, 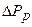 =
= 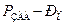 репрессия, равная разности забойного и пластового давлений.
репрессия, равная разности забойного и пластового давлений.

Следует отметить, что для нетронутого массива σr и σθ , при условии r 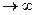 , должны быть равны
, должны быть равны  .
.
Действительно, проверка равенств (3.4) показывает:
при r = 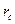
 а; при
а; при 

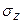
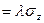 ;
;
| |
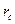
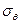 = 2
= 2 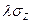 - а; при
- а; при 
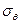 =
= 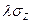 ,
,
Из теории упругости следует закономерность, состоящая в следующем: при действии в среде 2 – х главных взаимно перпендикулярных напряжений возникает сдвиговое напряжение 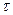 , которое равно
, которое равно 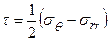 или
или 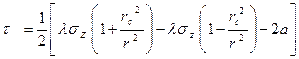 =
= 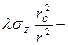
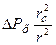 . (3.5)
. (3.5)
 Обозначим известное сдвиговое напряжение
Обозначим известное сдвиговое напряжение  , получим
, получим
 =
= 
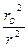
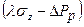 (3.6)
(3.6)
Для размера зоны дилатансии в пласте из (3.5) получим

 ( 3.7)
( 3.7)
Основная проблема состоит в определении значения предела прочности породы – коллектора на сдвиг  для конкретного пласта в условиях залегания.
для конкретного пласта в условиях залегания.
Дляописания объемных деформаций пористых сред в условиях пластического течения используется следующее реологическое уравнение
dθ = dθ ш - dθD = ß(Р)dp – λ(έr0,5)dτ , (3.8)
где θш–объемная деформация, обусловленная действием шаровой части тензора напряжений; θD–дилатантная составляющая объемной деформации среды; έr - второй инвариант девиатора тензора скоростей деформаций; λ–скорость дилатансии. Вычитаемое в правой части выражения представляет собой дилатантную составляющую деформации в функции от сдвигового напряжения. Переходя к теории конечных деформаций, величину θD можно представить в виде
θD = λ ( έr 0,5 )Δτ = Φ·Δ σр 0,5 , (3.9)
где Φ - некоторая функция, σр- второй инвариант девиатора тензора напряжений.
Дата добавления: 2016-02-02; просмотров: 562;
