Основные законы распределения, используемые в теории надежности

В теории надежности наибольшее распространение получили следующие законы распределения случайных величин f(t):

для дискретных случайных величин - биноминальный закон; закон Пуассона;

для непрерывных случайных величин - экспоненциальный закон; нормальный закон; гамма-распределение; закон Вейбулла; χ² - распределение; логарифмически-нормальное распределение.

Биноминальный закон распределения числа n появления события A в m независимых опытах (испытаниях). Если вероятность появления события A в одном испытании равна p, вероятность непоявления события A равна q=1-p; число независимых испытаний равно m, то вероятность появления n событий в испытаниях будет

, (4.3.2)

где 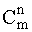- число сочетаний из m по n.

Свойства распределения следующие:

1) число событий n - целое положительное число;

2) математическое ожидание числа событий равно mp;

3) среднеквадратическое отклонение числа событий

.

При увеличении числа испытаний биноминальное распределение приближается к нормальному со средним значением n/m и дисперсией p(1-p)/m.

Закон Пуассона - распределение чисел случайного события n_i за время τ. Вероятность возникновения случайного события n раз за время τ

P_n(τ) = 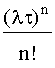exp(-λτ), (4.3.3)

где λ - интенсивность случайного события.

Свойства распределения следующие:

1) математическое ожидание числа событий за время τ равно λτ;

2) среднеквадратическое отклонение числа событий

.

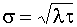Характерный признак распределения Пуассона - равенство математического ожидания и дисперсии. Это свойство используется для проверки степени соответствия исследуемого (опытного) распределения с распределением Пуассона.

Распределение Пуассона получается из биноминального распределения, если число испытаний m неограниченно возрастает, а математическое ожидание числа событий a=λτ остается постоянным.

Тогда вероятность 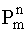биноминального распределения при каждом n, равном 0,1,2..., стремится к пределу

.

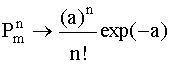Закон Пуассона используется тогда, когда необходимо определить вероятность того, что в изделии за заданное время произойдет один, два, три и т.д. отказов.

Экспоненциальный (показательный) закон распределения случайной величины X (рис. 4.3.3,а) записывается в общем случае так:

P(x) = еxp (-λx),

где P(x) - вероятность того, что случайная величина X имеет значение больше x; значения е^-х даются в прилож. 1.

В частном случае, когда за случайную величину принимается время работы объекта t, вероятность того, что изделие на протяжении времени t будет находиться в работоспособном состоянии, равна еxp(-λt):

P(t) = еxp(-λt), (4.3.4)

где λ - интенсивность отказов объекта для экспоненциального распределения (она постоянна), т.е λ = const.

Выражение (4.3.4) можно получить непосредственно из (4.3.3), если число отказов n принять равным 0.

Вероятность отказа за время t из (4.3.4)

Q(t) = 1 - P(t) = 1 - еxp (-λt). (4.3.5)

Плотность вероятности отказов

f(t) = ¶Q/¶t = λеxp (-λt). (4.3.6)

Рис. 4.3.3. Распределения: а – экспоненциальное;

б - γ-распределение; в - Вейбулла;

г - нормальное; д - усеченное нормальное;

е - Рэлея

Среднее время работы до возникновения отказа

. (4.3.7)

Дисперсия времени работы до возникновения отказа

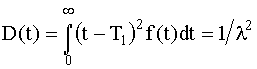. (4.3.8)

Среднеквадратическое время работы

σ(t) = T₁.

Равенство среднеквадратического отклонения среднему времени работы - характерный признак экспоненциального распределения.

Статистические материалы об отказах элементов свидетельствуют о том, что в основном время их работы подчиняется экспоненциальному закону распределения. Условием возникновения экспоненциального закона распределения времени до отказа служит постоянство интенсивности отказов, что характерно для внезапных отказов на интервале времени, когда период приработки объекта закончился, а период износа и старения еще не начался, т.е. для нормальных условий эксплуатации. Постоянной становится интенсивность отказов сложных объектов, если вызываются они отказами большого числа комплектующих элементов.

Время возникновения первичных отказов может быть расположено на оси времени так, что суммарный поток отказов сложного изделия становится близким к простейшему, т.е. с постоянной интенсивностью отказов.

Этими обстоятельствами, а также тем, что предположение об экспоненциальном распределении существенно упрощает расчеты надежности, объясняется широкое применение экспоненциального закона в инженерной практике.

Гамма-распределение случайной величины (рис. 4.3.3,б). Если отказ устройства возникает тогда, когда произойдет не менее k отказов его элементов, а отказы элементов подчинены экспоненциальному закону с параметрами λ₀, плотность вероятности отказа устройства

f(t) = 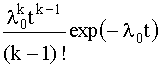, (4.3.9)

где λ₀ - исходная интенсивность отказов элементов устройства, отказ которого вызывается отказом k элементов.

Этому распределению подчиняется время работы резервированных устройств. Равенство (4.3.9) получается из (4.3.3).

Вероятность k и более отказов, т.е. вероятность отказа данного устройства,

P(n³k) = 1 - 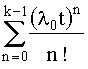ехp(- λ₀t). (4.3.10)

Плотность вероятности отказа устройства за время t

f(t)= 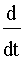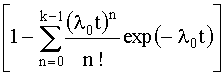= 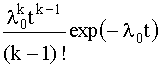. (4.3.11)

Среднее время работы устройства до отказа

T₁ = kT₀ = k/λ₀. (4.3.12)

Интенсивность отказов устройства

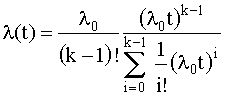. (4.3.13)

Вероятность безотказного состояния устройства

P(t) = еxp(-λ₀t) 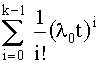. (4.3.14)

При k = 1 γ-распределение совпадает с экспоненциальным распределением.

При увеличении k γ-распределение будет приближаться к симметричному распределению, а интенсивность отказов будет иметь все более выраженный характер возрастающей функции времени.

Распределение Вейбулла. Для случая, когда поток отказов не стационарный, т.е. плотность потока изменяется с течением времени, функция распределения времени до отказа приобретает вид, показанный на рис. 4.3.3,в.

Плотность вероятности отказов этого распределения:

f(t) = λαt^α-1еxp(-λ₀t^α). (4.3.15)

Вероятность отсутствия отказа за время t

P(t) = еxp(-λ₀t^α). (4.3.16)

Интенсивность отказов

λ(t) =αλ_t^α-1. (4.3.17)

В (4.3.15) - (4.3.17) α и λ₀ - параметры закона распределения. Параметр λ₀ определяет масштаб, при его изменении кривая распределения сжимается или растягивается. При α = 1 функция распределения Вейбулла совпадает с экспоненциальным распределением; при α < 1 интенсивность отказов будет монотонно убывающей функцией; при α > 1 - монотонно возрастающей. Это обстоятельство дает возможность подбирать для опытных данных наиболее подходящие параметры α и λ₀, с тем чтобы уравнение функции распределения наилучшим образом совпадало с опытными данными. Распределение Вейбулла имеет место для отказов, возникающих по причине усталости тела детали или поверхностных слоев (подшипники, зубчатые передачи). Этот случай связан с развитием усталостной трещины в зоне местной концентрации напряжений, технологического дефекта или начального повреждения. Период времени до зарождения микротрещины характеризуется признаками внезапного отказа, а процесс разрушения - признаками износового отказа.

Этот закон применим для отказов устройства, состоящего из последовательно соединенных дублированных элементов и других подобных случаев.

Это распределение иногда используется для описания надежности подшипников качения (α = 1,4 - 1,7).

Средняя наработка до первого отказа определится из следующего выражения:

T = 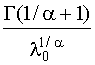. (4.3.18)

Значения Г (гамма-функции) табулированы (прилож. 2).

Нормальное распределение (рис. 4.3.3,г) случайной величины X возникает всякий раз, когда X зависит от большого числа однородных по своему влиянию случайных факторов, причем влияние каждого из этих факторов по сравнению с совокупностью всех остальных незначительно. Это условие характерно для времени возникновения отказа, вызванного старением, т.е. этот закон используется для оценки надежности изделий при наличии постепенных (износовых) отказов.

Плотность вероятности отказов

f(t) = 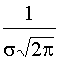еxp[-(t-T)²/2σ²], (4.3.19)

где T - средняя наработка до отказа; σ - среднее квадратическое (стандартное) отклонение времени безотказной работы.

Вероятность отказа время t

F(t)= 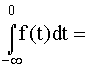еxp[-(t-T)²/2σ²]. (4.3.20)

Значение функции распределения определяется формулой

F(t) = 0,5 + Ф(u) = Q(t); u = (t-T) / σ. (4.3.21)

Вероятность отсутствия отказа за время t

P(t) = 1-Q(t) = 1-[0,5+Ф(u)] = 0,5 - Ф(u). (4.3.22)

Значения F(t) табулированы (прилож. 3).

График λ(t) показан на рис. 4.3.3,г. Интенсивность отказов монотонно возрастает и после T начинает приближаться к асимптоте:

y = (t-T) / σ. (4.3.23)

Монотонное возрастание интенсивности отказов с течением времени - характерный признак нормального распределения. Нормальное распределение существенно отличается от экспоненциального. Началом отсчета времени t в (4.3.20) служит начало эксплуатации объекта, т.е. момент, когда начинается процесс износа и старения, а началом отсчета в (4.3.4) - момент времени, когда установлено, что изделие исправно (этот момент может быть расположен в любой точке на оси времени).

Усеченное нормальное распределение (рис. 4.3.3, д). Так как при нормальном распределении случайная величина может принимать любые значения от -¥ до +¥, а время безотказной работы может быть только положительным, следует рассматривать усеченное нормальное распределение с плотностью вероятности отказов

f(t) = еxp[-(t-T₁)²/2σ²]. (4.3.24)

Нормирующий множитель c определяется из выражения

c 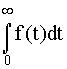= 1 (4.3.25)

и равен

c = 1/F(T₁/σ) = 1/[0,5+Ф₀(T₁/σ)], (4.3.26)

где F(T₁/σ) = 1/2π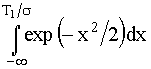 (4.3.27)

- табулированная (прилож. 4) интегральная функция нормального распределения;

Ф₀(T₁/σ) = 1/2π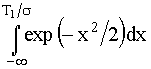 (4.3.28)

- нормированная функция Лапласа.

Тогда (3.24) запишется следующим образом:

f(t) = еxp[-(t-T₁)²/2σ²]. (4.3.29)

Средняя наработка до отказа в усеченном распределении и параметр T₁ неусеченного нормального распределения связаны зависимостью

T = T₁ + f(t) = 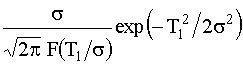. (4.3.30)

При T/σ ³ 2, что имеет место в абсолютном большинстве случаев при оценке надежности устройств с нормально распределенными отказами, коэффициент c мало отличается от единицы и усеченное нормальное распределение достаточно точно аппроксимируется обычным нормальным законом.

Вероятность безотказной работы определяется из выражения

P(t) = 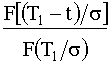. (4.3.31)

Интенсивность отказов находится из

λ(t) = 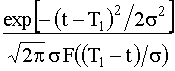. (4.3.32)

Распределение Рэлея (рис. 4.3.3,е) - непрерывное распределение вероятностей с плотностью

p(x) = x/σ² exp(-x²/2σ²) при x > 0;

p(x) = 0 при x£0,

зависящей от масштабного параметра σ > 0. Распределение имеет положительную асимметрию, его единственная мода находится в точке x = σ. Все моменты распределения Рэлея конечны.

Также как и распределение Вейбулла или γ-распределение, распределение Рэлея пригодно для описания поведения изнашивающихся или стареющих изделий.

Частота отказов (функция плотности распределения вероятности отказов) определяется:

f(t) = t/σ² еxp(-t²/2σ²). (4.3.33)

Вероятность безотказной работы вычисляется из выражения

P(t) = еxp(-t²/2σ²). (4.3.34)

Интенсивность отказов находится из

λ(t) = t/σ². (4.3.35)

Средняя наработка до первого отказа составит

Т= . (4.3.36)