Изображение состава СИСТЕМЫ.

Трехкомпонентные системы.

Растворы, содержащие три компонента, удобнее рассматривать, пользуясь диаграммой, отображающей содержание каждого из компонентов системы. Для этого могут быть использованы различные формы графиков.

Часто пользуются равносторонним треугольником – треугольником Гиббса:

В каждой вершине треугольника располагается чистое вещество: точка А – чистое вещество А (100 %). Каждая сторона треугольника характеризует двухкомпонентный состав, например, сторона АС характеризует состав раствора АС. Из каждой вершины треугольника опущен перпендикуляр: Аа, Вв, Сс. Перпендикуляры обычно разбивают на 100 или 10 частей, тогда точка А – 100 % вещества А, точка а – 0 % вещества А.

Рассмотрим фигуративную точку К, лежащую внутри области треугольника. Из этой точки на каждую сторону треугольника опускаем перпендикуляр.

Содержание вещества А пропорционально длине отрезка КМ, т.е. отрезка, находящегося на противоположной стороне треугольника от данной вершины.

Вещество А → KM

Вещество В → KN

Вещество С → KL

Сумма длин этих отрезков равна длине перпендикуляра, например: Аа=100%= KM+KN+КL.

Треугольник Розебума:

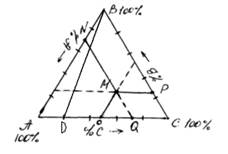
Каждую сторону треугольника делят на 100 или 10 равных частей, получая процентное содержание компонентов двухкомпонентной смеси.

Рассмотрим фигуративную точку М. Проведем через точку М прямые, параллельные сторонам треугольника. Процентное содержание компонента А определяется отрезком МР (точка Р лежит на стороне ВС).

Вещество А → MР

Вещество В → MО

Вещество С → MN

Треугольные диаграммы Розебума основаны на следующем свойстве: сумма отрезков прямых, проведенных параллельно сторонам равностороннего треугольника через любую точку, лежащую внутри этого треугольника, есть величина постоянная, равная стороне треугольника: MР + MО + MN=АВ=ВС=АС=100%.

Метод Розебума получил более широкое применение, так как он позволяет судить о содержании в системе всех трех компонентов по делениям, нанесенным на одной стороне треугольника.

Так, принимая сторону АС за 100 % и учитывая, что MP=QC, MО=ОQ, MN=АО, получим состав, изображенный фигуративной точкой М:

Вещество А =QC

Вещество В =QО

Вещество С =АО

Точки, лежащие на прямой BD, проходящей через вершину треугольника (В), изображают составы системы с постоянным соотношением концентраций двух других компонентов А и С; А:С=80:20=4:1.