ДИАГРАММЫ СОСТОЯНИЯ ДВОЙНЫХ ЖИДКИХ СИСТЕМ

Законы Коновалова.

На практике возникает необходимость не только перевести вещества в растворенное состояние, но и разделить жидкие растворы на составляющие их компоненты.

Наиболее распространенные методы разделения жидких однородных растворов, состоящих из летучих компонентов – это перегонка и ректификация. Их широко применяют в промышленности. Теоретической основой процесса разделения жидких растворов, состоящих из летучих компонентов, являются законы Коновалова (или Гиббса – Коновалова).

Законы Коновалова устанавливают связь между составом жидкого раствора смеси летучих компонентов и составом насыщенного равновесного с ним пара в зависимости от температуры и давления.

В равновесной двухкомпонентной системе сумма мольных долей компонентов в жидкой (N 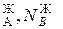) и паровой (N 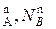) фазах равна единице, т.е.

N 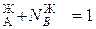; N (*)

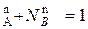Подчеркнем, что эти условия и весь ход дальнейших рассуждений справедливы для жидких растворов двух летучих компонентов, причем пар, находящихся в равновесии с жидким раствором, содержит оба компонента. Летучим компонентом называют жидкость, которая при данной температуре имеет достаточно высокое давление пара. К числу жидких растворов из летучих компонентов относятся продукты перегонки нефти (бензин, керосин и др.).

Условия (*) не означают, что составы жидкости и находящегося в равновесии с ней пора совпадают, т.е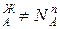. N и N 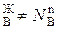. Эти неравенства отражают суть первого закона Коновалова. Для его уяснения обратимся к рисунку.

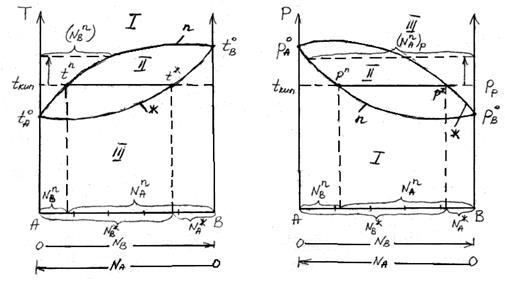
В соответствии с правилом фаз Гиббса в двух компонентной равновесной системе из четырех параметров (температура, давление, составы обеих фаз) только два являются независимыми (Т и р). При заданных значениях Т и р в равновесии находятся жидкость и пар фиксированного состава. Если же из двух независимых величин одна не изменяется (р=const или Т=const), то температура в первом случае и давление во втором однозначно определяются составом любой из существующих фаз.

Равновесие между раствором и паром удобно рассматривать в виде диаграмм, выражающих зависимость от состава системы температуры кипения жидкости (при р=const) или давления пара (при Т=const) . На диаграмме состояния по оси абсцисс справа на лево отложена мольная доля компонента, имеющего в чистом виде более низкую температуру кипения (на нашем первом рисунке компонент А более летуч, t 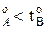) и более высокое давление насыщенного пара (на втором рисунке р ).

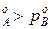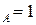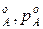Концевые точки оси абсцисс соответствуют чистым компонентам N ,t и N 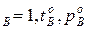. У раствора мольная доля компонентов А и В изменяется в диапазоне 0<N<1.

На рисунке следует различать кривую пара, обозначенную “n”, и кривую жидкости – « ж». Фигуративные точки (т. е. точки на диаграмме состояния системы, которые определяют состав, фазовое состояние и параметры (температуру, давление) системы, лежащие на кривой жидкости, характеризуют состав кипящей при данной температуре жидкости (а) или состав жидкости, кипящей при данном давление (б). Фигуративные точки на кривой пара позволяют определить состав пара при тех же условиях.

Кривые пара и жидкости разделяют диаграмму состояния системы на три области. Две из них, области пара I и жидкости III, являются гомогенными, а область II отражает гетерогенное состояние системы. В гомогенных областях, согласно правилу фаз Гиббса c=k-ф+2, двухкомпонентная система имеет две степени свободы: состав – температура (при p=const, рис.а) и состав – давление (при t=const,рис.б).

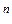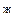Воспользуемся диаграммами рисунков а и б и определим состав жидкости и пара. Для этой цели проведем на диаграмме прямые t – t и p 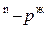; параллельные оси абсцисс и характеризующие температуру кипения и парциальное давление насыщенного пара системы. Фигуративные точки пересечения этих прямых с кривыми пара и жидкости (t 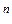и p 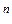и соответственно t 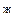и 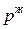) будут определять равновесный состав пара и жидкости двухкомпонентной системы.

По оси абсцисс на диаграммах зафиксированы составы жидкой и парообразной фаз этой системы, а именно:

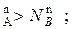N N *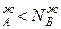

Условия (*) отражают первый закон Коновалова, который имеет несколько формулировок. Приведем некоторые из них:

в условиях равновесия относительное содержание компонента в паровой фазе отличается от содержания этого компонента в жидком растворе;

в паре содержится больше того компонента, добавление которого в раствор понижает температуру кипения или повышает давление насыщенных паров;

пар обогащается более летучим компонентом.

Если повысить температуру кипения (это повышение на диаграмме показано стрелкой), то в паре повышается мольная доля компонента В [ 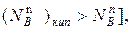т.е. того компонента, которого в составе пара меньше, чем в жидком растворе. При увеличении давления пара (это увеличение до p 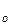на диаграмме б показано стрелкой) возрастает мольная доля компонента A [ 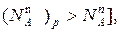т.е. того компонента, которого в паровой фазе больше.

На основании этих соображений помимо приведенных формулировок суть первого закона Коноваловаможно представить следующим образом:

при постоянном давлении(p=const,a) температура кипения раствора возрастает при увеличении концентрации компонента, содержание которого в паре меньше, чем в растворе;

при постоянной температуре (t=const,б) давление пара над раствором возрастает при увеличении концентрации компонента, содержание которого в паре больше, чем в растворе.

Представленные диаграммы справедливы для растворов, подчиняющихся закону Рауля или, по крайней мере, при незначительных отклонениях от этого закона. Причем, зависимости температуры кипения и давления пара от состава системы имеют противоположный вид, являясь зеркальным отображением.

У приведенных выше диаграмм отсутствуют максимумы и минимумы, что характерно для идеальных растворов. В случае больших отклонений от закона Рауля (диаграммы 3и 4) на диаграммах состояния появляются максимумы и минимумы.

Диаграммы состояния «жидкость – пар» двухкомпонентной системы с азеотропными точками при постоянном давлении (а) и t=const (б).

Экстремумы соответствуют точкам О, в которых состав жидкости и пара одинаков. В этих точках, называемых азеотропными, пересекаются кривые жидкости и пара:

N ,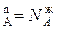

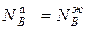
На рисунке а приведена диаграмма, соответствующая максимуму температуры кипения в азеотропной точке, а на рис.б – минимуму давления пара; максимум на диаграмме t–N отвечает минимуму на диаграмме P-N. Возможен и другой вариант, когда минимуму на кривой температуры кипения соответствует максимум на кривой давления. В любых вариантах на подобных диаграммах имеются азеотропные точки (точки О), которые соответствуют нераздельнокипящим смесям.

Диаграмма состояния, характеризующаяся наличием азеотропной точки, отвечает второму закону Коновалова. Как и первый закон, он имеет несколько формулировок. Приведу лишь одну из них, наиболее часто встречающуюся и более общую:

точки экстремума на кривых температуры кипения (при p=const) или на кривых давления (при t=const) соответствуют раствором, состав жидкости которых одинаков с составом равновесного с ней пара.

В условиях равновесия азеотропная смесь испаряется как чистое вещество.

Законы Коновалова справедливы вдали от критического состояния двухфазной системы (оно соответствует точке k на диаграмме состояния воды), когда находящиеся в равновесии жидкость и ее насыщенный пар становится тождественными по всем параметрам (система становится гомогенной).

Например, для воды критическими параметрами являются температура 647,3 К, давление 221,206 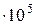и мольный объем 56 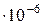м 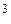/моль.

Первоначально законы Коновалова рассматривались применительно к двухкомпонентным системам, образующим жидкую и паровую фазы. Впоследствии было установлено, что эти законы при определенных условиях можно распространить и на многокомпонентные системы. Закономерности, определяемые ими, можно применить к равновесному состоянию твердое тело – пар и твердый раствор – жидкий раствор.

ДИАГРАММЫ СОСТОЯНИЯ ДВОЙНЫХ ЖИДКИХ СИСТЕМ