Сетевой закон Амдала

Закон Амдала. Одной из главных характеристик параллельных систем является ускорение R параллельной системы, которое определяется выражением:

R = T₁ / T_n,

где T₁ – время решения задачи на однопроцессорной системе, а T_n – время решения той же задачи на n-процессорной системе.

Пусть W = W_СК + W_ПР, где W_СК – общее число операций в задаче, W_ПР – число операций, которые можно выполнять параллельно, а W_СК – число скалярных (нераспараллеливаемых) операций.

Обозначим также через t время выполнения одной операции. Тогда получаем известный закон Амдала:

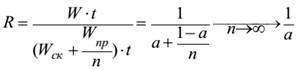(1.3)

Здесь a = W_СК / W – удельный вес скалярных операций.

Закон Амдала определяет принципиально важные для параллельных вычислений положения:

1. Ускорение зависит от потенциального параллелизма задачи (величина 1-а) и параметров аппаратуры (числа процессоров n).

2. Предельное ускорение определяется свойствами задачи.

Пусть, например, a=0.2 (что является реальным значением), тогда ускорение не может превосходить 5 при любом числе процессоров, то есть максимальное ускорение определяется потенциальным параллелизмом задачи. Очевидной является чрезвычайно высокая чувствительность ускорения к изменению величины а.

Сетевой закон Амдала. Основной вариант закона Амдала не отражает потерь времени на межпроцессорный обмен сообщениями. Эти потери могут не только снизить ускорение вычислений, но и замедлить вычисления по сравнению с однопроцессорным вариантом. Поэтому необходима некоторая модернизация выражения (1.3). Перепишем (1.3) следующим образом:

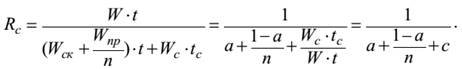(1.4)

Здесь W_С – количество передач данных, t_С – время одной передачи данных. Выражение

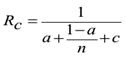(1.5)

и является сетевым законом Амдала. Этот закон определяет следующие две особенности многопроцессорных вычислений:

1. Коэффициент сетевой деградации вычислений с:

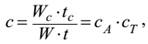(1.6)

определяет объем вычислений, приходящийся на одну передачу данных (по затратам времени). При этом с_А определяет алгоритмическую составляющую коэффициента деградации, обусловленную свойствами алгоритма, а с_Т – техническую составляющую, которая зависит от соотношения технического быстродействия процессора и аппаратуры сети. Таким образом, для повышения скорости вычислений следует воздействовать на обе составляющие коэффициента деградации. Для многих задач и сетей коэффициенты с_А и с_Т могут быть вычислены аналитически и заранее, хотя они определяются множеством факторов: алгоритмом задачи, размером данных, реализацией функций обмена библиотеки MPI, использованием разделяемой памяти и, конечно, техническими характеристиками коммуникационных сред и их протоколов.

2. Даже если задача обладает идеальным параллелизмом, сетевое ускорение определяется величиной

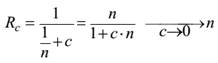(1.7)

и уменьшается при увеличении числа процессоров. Следовательно, сетевой закон Амдала должен быть основой оптимальной разработки алгоритма и программирования задач, предназначенных для решения на многопроцессорных ЭВМ.

Лекция 2