Развертка поверхности треугольной пирамиды
Развертка боковой поверхности пирамиды (рис. 9.3) состоит из трех треугольников, представляющих в истинном виде боковые грани пирамиды.
Для построения развертки необходимо предварительно определить истинные длины боковых ребер пирамиды. Повернув эти ребра вокруг высоты пирамиды до положения параллельного плоскости p2, на фронтальной плоскости проекций получим их истинные длины в виде отрезков 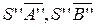 и
и 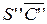 .
.
Построив по трем сторонам 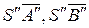 и
и 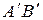 грань пирамиды ASB (рис. 9.4) пристраиваем к ней смежную грань – треугольник BSC, а к последнему грань CSA. Полученная фигура представит собою развертку боковой поверхности данной пирамиды.
грань пирамиды ASB (рис. 9.4) пристраиваем к ней смежную грань – треугольник BSC, а к последнему грань CSA. Полученная фигура представит собою развертку боковой поверхности данной пирамиды.
Для получения полной развертки к одной из сторон основания пристраиваем основание пирамиды – треугольник АВС.
Для построения на развертке линии, по которой поверхность пирамиды пересечется плоскостью a (рис. 9.3), надлежит нанести на ребра SA, SB и SC, соответственно, точки 1, 2 и 3, в которых эта плоскость пересекает ребра, определив истинные длины отрезков S1, S2 и S3.
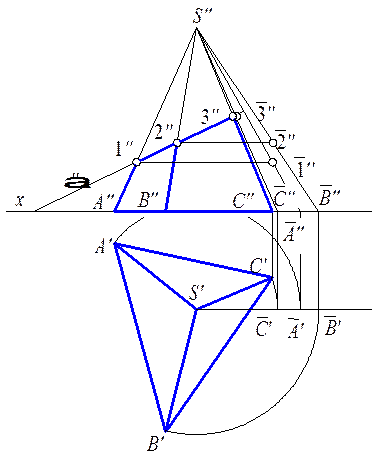
Рис. 9.3

Рис. 9.4
Дата добавления: 2016-02-02; просмотров: 1556;
