Пассивные элементы R, L, C в цепи синусоидального тока

Резистивный элемент

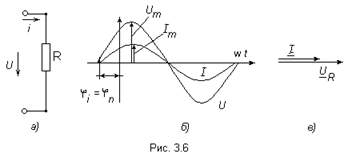
В электрической цепи с резистивным элементом R ток изменяется по синусоидальному закону с начальной фазой 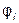, то есть

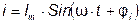. (3.12)

Напряжение на зажимах резистора

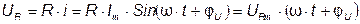; (3.13)

где 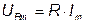- амплитудное значение напряжения на зажимах резистора, 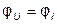- начальные фазы напряжения и тока.

Кривые изменения напряжения 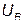и тока 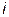(рис. 3.6б) в один и тот же момент времени t достигают максимального значения и одновременно проходят нулевые значения. Иначе говоря, обе кривые совпадают по фазе (рис. 3.6в).

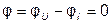. (3.14)

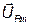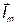Векторы и совпадают по направлению (угол ). Переходя к действующим значениям можно записать

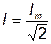; (3.15)

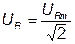. (3.16)

Сопротивление переменному току будет больше, чем постоянному за счет неравномерного распределения тока в проводе и потерь энергии в окружающую среду. Поэтому в отличие от сопротивления постоянному току сопротивление R в цепи переменного тока называется активным.

Индуктивный элемент.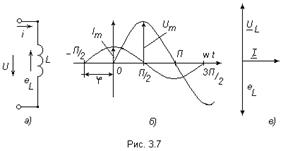

Изменение тока в цепи с индуктивностью L (рис. 3.7а) вызывает возникновение Э.Д.С. самоиндукции 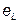, которая по закону Ленца противодействует изменению тока. При увеличении тока Э.Д.С. 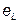действует навстречу току, а при уменьшении - в направлении тока, противодействуя его изменению. Показанные на рис. 3.7а положительные направления 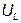и 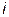имеют место только в течение некоторого узкого промежутка времени. Для тока, изменяющегося по гармоническому закону 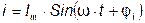и при 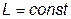Э.Д.С. самоиндукции

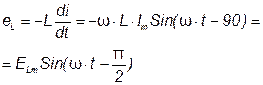(3.17)

Чтобы в цепи протекал ток, требуется иметь на зажимах напряжение, уравновешивающее Э.Д.С. самоиндукции, равное ей по значению и противоположное по знаку.

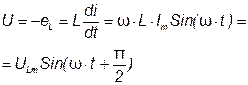(3.18)

где 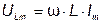- амплитуда напряжения.

Произведение 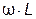обозначается 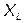, называется индуктивным сопротивлением и измеряется в Омах:

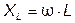. (3.19)

Из выражения 3.18 следует, что на участке цепи с индуктивностью L напряжение опережает ток на четверть периода ( 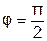). На рис. 3.7в вектор напряжения 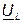опережает вектор тока 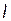на 90⁰, а комплекс (вектор) Э.Д.С. самоиндукции 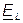находится в противофазе с комплексом напряжения .

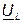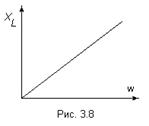
Кроме того, из соотношения 3.19 можно заметить, что индуктивное сопротивление пропорционально 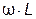(рис. 3.8).

Если R =0, то средняя активная мощность равна 0:

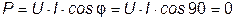. (3.20)

Временная диаграмма напряжения и тока показана на рис. 3.7б.

Емкостной элемент.

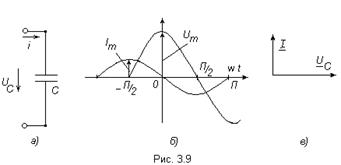
В цепи с конденсатором (рис. 3.9а), включенным на напряжение переменного тока, происходит непрерывное перемещение электрических зарядов.

Мгновенный ток в цепи равен скорости изменения заряда конденсатора:

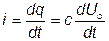, (3.21)

где q – заряд конденсатора, Кл;

С – ёмкость конденсатора, Ф.

Если напряжение на зажимах конденсатора изменяется по синусоидальному закону:

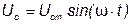, (3.22)

то ток в цепи

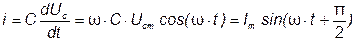, (3.23)

где 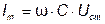- амплитуда тока.

Величина 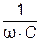, измеряемая в единицах сопротивления и обозначаемая 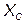, называется ёмкостным сопротивлением цепи:

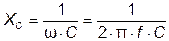. (3.24)

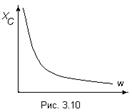
Емкостное сопротивление обратно пропорционально частоте приложенного напряжения (рис. 3.10).

Из сопоставления 3.22 и 3.23 видно, что ток через конденсатор опережает по фазе напряжение на конденсаторе на 90⁰ (рис. 3.9б,в).

На основании выражения 3.23 определяется связь между действующими значениями напряжения и тока:

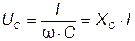, (3.25)

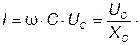(3.26)

Выше были рассмотрены идеализированные модели катушек и конденсаторов, у которых R=0. На практике изготовить их такими невозможно, и этими научными абстракциями пользуются для того, чтобы ясно представить себе свойства таких элементов.