Погрешность установки заготовки

Производственными погрешностями, под влиянием которых возникает эта составляющая погрешности исходного размера, являются погрешности самой обрабатываемой детали (заготовки) и погрешности установочных элементов приспособления. Зная погрешности детали (из операционных карт предшествующих операций) и погрешности установочных элементов (из чертежей на приспособление), можно рассчитать величину погрешности D_уз для каждого исходного размера. Как правило, расчет сводится к решению вполне определенной геометрической задачи. Можно привести следующий пример (рис. 3.20).

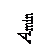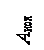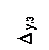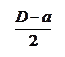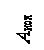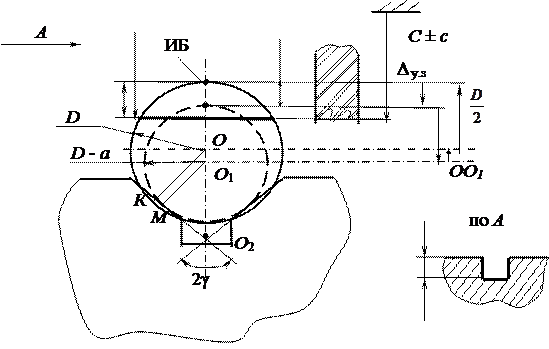Рис. 3.20. Пример задачи определенияD_уз (пояснения в тексте)

Допустим в детали цилиндрической формы фрезеруется паз. Деталь устанавливаем в призме, операция настроена. Поскольку диаметр детали будет колебаться в пределах от D до D – a, то положение исходной базы, от которой измеряется размер А, будет перемещаться в пределах D_уз. Это перемещение будет зависеть также от точности изготовления установочных элементов приспособления, в частности, от точности угла g. Задача заключается в том, чтобы найти численное значение величины D_уз. Геометрическое представление задачи приведено на рис. 3.20. Из рисунка и из схемы размерной цепи можно записать уравнение размерной цепи:

D_уз + 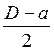– ОО₁ – 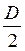= 0 , (3.10)

из которого

D_уз = ОО₁+ 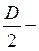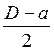. (3.11)

Из двух прямоугольных треугольников ОКО₂ и О₁МО₂ можно записать:

ОО₁ = ОО₂ – О₁О₂, (3.12)

Здесь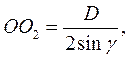

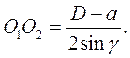
Подставив в (3.12), получим

ОО₁ = 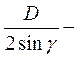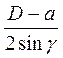= 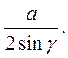(3.13)

Теперь возможно решение уравнения (3.11):

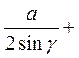
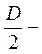
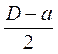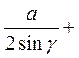
D_уз = = 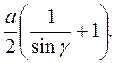(3.14)

В общем виде задачи подобного вида не бывают сложными, но общее их количество чрезвычайно большое. Поэтому разработаны некоторые общие зависимости для расчета D_уз.

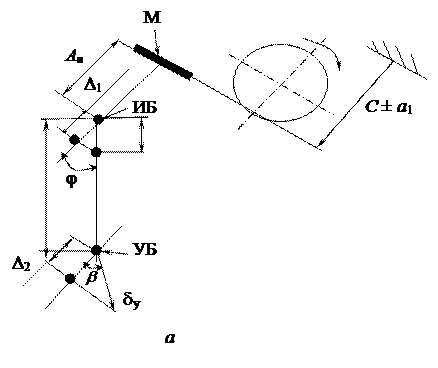
Случай несовмещения баз. На рис. 3.21 показана упрощенная схема такого случая. Чтобы не усложнять чертеж, условно показана обрабатываемая поверхность М в условиях настроенной операции: инструмент всегда будет находиться по отношению к обрабатываемой поверхности (для разных деталей) на расстоянии С±а₁. Исходная база ИБ и установочная база УБ условно показаны точками. На рис. 3.21, б в качестве примера показан вариант обработки реальной детали.

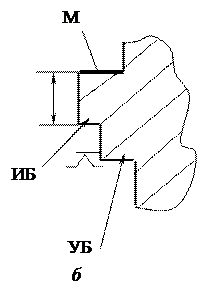Рис. 3.21. К вопросу определения D_уз при несовмещении ИБ и УБ(пояснения в тексте)

Задача состоит в том, чтобы расчетным путем определить погрешность исходного размера А_и, связанную с установкой детали - D_уз. Из схемы видно, что точность размера А_и будет зависеть от того, какое положение займет исходная база. Смещение ИБ будет происходить вследствие наличия размера S, выполненного с допуском а, и погрешности установки d_у. Величина D_уз определится как

D_уз = D₁ + D₂ = а cosj + d_у cosb

Составляющая D₁ называется погрешностью от несовмещения исходной и установочной баз. Как можно видеть, она совершенно не зависит от процесса и от приспособления. Составляющая D₂ называется расчетной погрешностью установки. Будучи функцией погрешности установки и угла b, она может регулироваться при проектировании установочных элементов приспособлений.

Вследствие взаимной независимости факторов, вызывающих возникновение составляющих D₁ и D₂, эти две составляющие не могут компенсировать одна другую, т.е. независимо от направления и знака допуска считают:

D_уз = | D₁| + |D₂|.

Случай совмещения баз. При совмещении исходной и установочной баз погрешность D₁ исчезает (рис. 3.22). Поэтому погрешность исходного размера будет зависеть от точности установки заготовки

D_уз = D₂ = d_у cosb.

Известны случаи неполного совмещения баз: это когда установочная база – цилиндрическая поверхность, а исходная база – образующая этой поверхности. Особенностью неполного совмещения баз является возможность взаимной компенсации двух погрешностей.

Рис. 3.22. К вопросу определенияD_узпри совмещении баз(пояснения в тексте)