Классификация кинематических пар
Прикладная механика
СТРУКТУРА И КЛАССИФИКАЦИЯ МЕХАНИЗМОВ
Структура механизмов
В состав механизмов входят твёрдые тела, которые называют звеньями. Звенья могут быть и не твёрдыми (например, ремень). Жидкости и газы в гидро- и пневмомеханизмах звеньями не считаются.
Условное изображение звеньев на кинематических схемах механизмов регламентируется ГОСТом. Примеры изображения некоторых звеньев приведены на рис. 1.1.
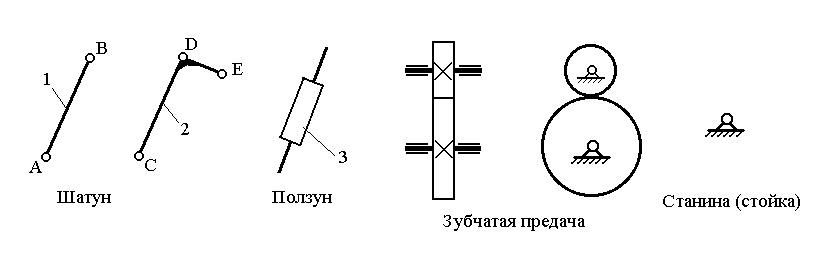 Рис. 1.1. Примеры изображения звеньев
Рис. 1.1. Примеры изображения звеньев
на кинематических схемах механизмов
Звенья бывают:
– входные (ведущие) – отличительным признаком их является то, что элементарная работа приложенных к ним сил положительна (работа силы считается положительной, если направление действия силы совпадает с направлением движения точки её приложения или под острым углом к ней);
– выходные (ведомые) – элементарная работа приложенных к ним сил является отрицательной (работа силы считается отрицательной, если направление действия силы противоположно направлению движения точки её приложения);
– подвижные;
– неподвижные (станина, стойка).
На кинематических схемах звенья обозначаются арабскими цифрами:0, 1, 2 и т.д. (см. рис. 1.1).
Подвижное соединение двух соприкасающихся звеньев называется кинематической парой. Она допускает возможность движения одного звена относительно другого.
Классификация кинематических пар
1. По элементам соединения звеньев кинематические пары делятся:
– на высшие (они имеются, например, в зубчатых и кулачковых механизмах) – соединение звеньев друг с другом происходит по линии или в точке:

– низшие – соединение звеньев друг с другом происходит по поверхности. В свою очередь низшие соединения делятся:
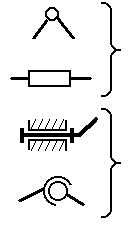
на вращательные
| в плоских механизмах; |
поступательные
цилиндрические
| в пространственных механизмах. |
сферические
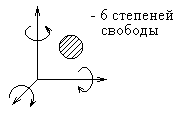
2. По количеству наложенных связей. Тело, находясь в пространстве (в декартовой системе координат X, Y, Z) имеет 6 степеней свободы. Оно может перемещаться вдоль каждой из трёх осей X, Y и Z, а также вращаться вокруг каждой оси (рис. 1.2). Если тело (звено) образует с другим телом (звеном) кинематическую пару, то оно теряет одну или несколько из этих 6 степеней свободы.
По количеству утраченных телом (звеном) степеней свободы кинематические пары делят на 5 классов. Например, если телами (звеньями), образовавшими кинематическую пару, утрачено по 5 степеней свободы каждым, эту пару называют кинематической парой 5-го класса. Если утрачено 4 степени свободы – 4-го класса и т.д. Примеры кинематических пар различных классов приведены на рис. 1.2.
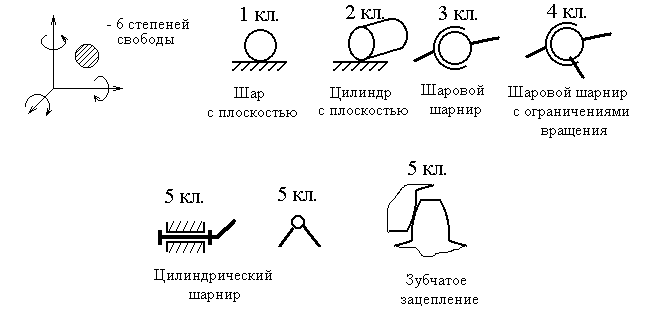 Рис. 1.2. Примеры кинематических пар различных классов
Рис. 1.2. Примеры кинематических пар различных классов
По структурно-конструктивному признакукинематические пары можно разделить на вращательные, поступательные, сферические, цилиндрические и др.
Кинематическая цепь
Несколько звеньев, соединённых между собой кинематическими парами, образуют кинематическую цепь.
Кинематические цепи бывают:
замкнутые
простые;
разомкнутые
| сложные. . |
Чтобы из кинематической цепи получить механизм, необходимо:
– одно звено сделать неподвижным, т.е. образовать станину (стойку);
– одному или нескольким звеньям задать закон движения (сделать ведущими) таким образом, чтобы все остальные звенья совершали требуемые целесообразные движения.
Число степеней свободы механизма – это число степеней свободы всей кинематической цепи относительно неподвижного звена (стойки).
Для пространственной кинематической цепи в общем виде условно обозначим:
количество подвижных звеньев –n,
количество степеней свободы всех этих звеньев–6n,
количество кинематических пар 5-го класса – P5,
количество связей, наложенных кинематическими парами 5-го класса на звенья, входящие в них, – 5Р5,
количество кинематических пар 4-го класса – Р4,
количество связей наложенных кинематическими парами 4-го класса на звенья, входящие в них, – 4Р4 и т.д.
| W = 6n – 5P5 – 4P4 – 3P3 – 2P2 – P1. |
Это структурная формула пространственной кинематической цепи, или формула Малышева, получена П.И. Сомовым в 1887 году и развита А.П. Малышевым в 1923 году.
Величину W называют степенью подвижности механизма (если из кинематической цепи образован механизм).
| W = 3n – 2P5 – P4. |
Эту формулу называют формулой П.Л. Чебышева (1869). Она может быть получена из формулы Малышева при условии, что на плоскости тело обладает не шестью, а тремя степенями свободы:
W = (6 – 3)n – (5 – 3)P5 – (4 – 3) P4 .
Величина W показывает, сколько должно быть у механизма ведущих звеньев (если W = 1 – одно, W = 2 – два ведущих звена и т.д.).
Дата добавления: 2016-01-30; просмотров: 1597;
