Треугольник сопротивлений

Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений

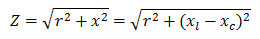
Ве́кторная диагра́мма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.Резонанс напряжений - резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.

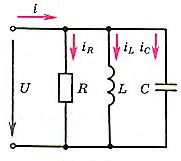
8. ля параллельного соединения RLC-элементов (рис. 1) справедливо уравнение первого закона Кирхгофа. Для комплексных токов:

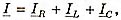
где 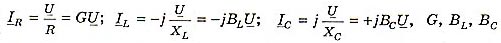- соответственно активная, индуктивная и емкостная проводимости отдельных ветвей цепи.

Электри́ческая проводи́мость (электропроводность, проводимость) — способность тела проводить электрический ток, а такжефизическая величина, характеризующая эту способность и обратная электрическому сопротивлению^[1]. В Международной системе единиц (СИ) единицей измерения электрической проводимости является сименс (русское обозначение: См; международное: S), определяемый как 1 См = 1 Ом^-1, то есть, как электрическая проводимость участка электрической цепи сопротивлением 1 Ом^[2]. Теперь возьмемпараллельноесоединение и построим треугольник проводимостей. Имеем:.Аналогично строим векторную диаграмму и треугольник проводимостей. Учитываем, что проводимость индуктивности отрицательна, поэтому угол междуибудет составлять. Поделив на, получаем треугольник проводимостей. Аналогично для активно-емкостной цепи.Вывод: Токи и напряжения – это вектора, проводимости и сопротивления – это отрезки.Кроме того, при помощи этих треугольников можно определить . Векторной диаграммой называется совокупность векторов на комплексной плоскости, соответствующая комплексным величинам и/или параметрам электрической цепи и их связям.Резонанс токов — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает ссобственной частотой контура.

9. В профессиональном лексиконе электрика наиболее популярны слова: фаза, ток, напряжение и словосочетание «косинус-фи». Этот «косинус-фи» всегда головная боль заводского энергетика. Попробуем популярно объяснить причину такого уважения электриков к тригонометрической функции cos φ. «Косинус-фи» в электроэнергетике еще называют коэффициентом мощности.
Коэффициент мощности характеризует потребителя электрической энергии с точки зрения наличия в нагрузке реактивной составляющей, при которой переменный ток и напряжение не совпадают по фазе. Коэффициент мощности показывает, насколько переменный ток в нагрузке сдвигается по фазе относительно напряжения на ней (отстает или опережает). Численно коэффициент мощности равен косинусу этого фазового сдвига. В электроэнергетике для коэффициента мощности принято обозначение cos φ (где φ — угол сдвига по фазе между током и напряжением). При наличии в нагрузке реактивной составляющей наряду со значением коэффициента мощности часто указывают и характер нагрузки: активно-ёмкостная или активно-индуктивная. Тогда коэффициент мощности называют соответственно опережающим или отстающим. Для начала следует подробно рассмотреть вопрос электрической мощности. В электрической цепи постоянного тока все просто и достаточно понятно. В такой цепи зная напряжение на зажимах потребителя и протекающий ток можем легко определить потребляемую мощность, умножив величину тока на напряжение:
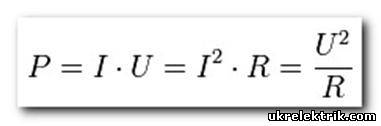п ри отсутствии таких приборов коэффициент мощности можно определить косвенным методом по показаниям трех приборов :амперметра, вольтметра и ваттметра. Тогда в однофазной цепи
cos φ = P / (U х I),
где Р, U, I - показания ваттметра, вольтметра и амперметра, соответственно.
В симметричной трехфазной цепи
cos φ = Pw / (√3 х Uл х Iл);
где Pw – активная мощность трехфазной системы,
Uл, Iл – соответственно линейные напряжение и ток. Компенсация реактивной мощности
Для уменьшения потерь, устранения перегрузок трансформаторов и линий электропередач прибегают к искусственному повышению коэффициента мощности электрических установок путем компенсации реактивной мощности непосредственно у потребителей с помощью батарей статических конденсаторов.

10.Соединим последовательно лампу накаливания с сопротивлением R, батарею конденсаторов с емкостью С и катушку с большой индуктивностью L. Если данную цепь присоединить к зажимам генератора переменного тока, то лампа загорится, что свидетельствует о наличии электрического тока в цепи, несмотря на разрыв, существующий между изолированными друг от друга обкладками конденсатора.
Для цепи переменного тока с последовательным соединением R, L, С (см. рисунок) дифференциальные уравнения по второму закону Кирхгофа имеют вид:

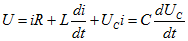
Здесь ток во всех трех участках один и тот же:

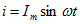
Разности потенциалов на всех трех сопротивлениях имеют вид:

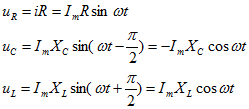
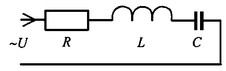
Решение системы дифференциальных уравнений можно существенно упростить, если перейти от дифференциальных уравнений к алгебраическим. Это можно сделать, изображая синусоидальные величины (i, u) в комплексной форме, т.е. в виде вектора на комплексной плоскости.

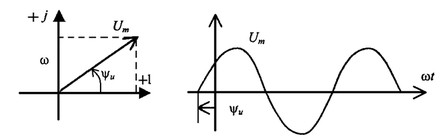
11. Для суждения о напряжениях между различными точками схемы полезны топографические диаграммы. Они представляют собой диаграммы комплексных потенциалов, причем каждой точке схемы соответствует определенная точка на топографической диаграмме. Точке отсчета, потенциал которой принят равным нулю, на топографической диаграмме соответствует начало координат.
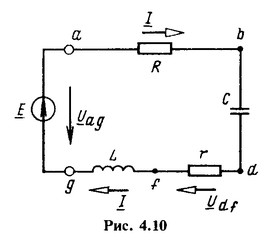Построим качественно топографическую диаграмму сначала для неразветвленной схемы, представленной на рис. 4.10. Отложим вектор тока I в произвольно выбранном направлении (рис. 4.11, а). Примем потенциал точки g равным нулю ( ) и определим потенциалы остальных точек.
Будем обходить схему, начиная от точки g, навстречу положительному направлению тока. Потенциал точки f больше потенциала точки g на падение напряжения на индуктивности: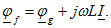
Так как 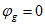, то потенциал 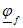изобразим вектором 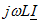. Конец этого вектора обозначим буквой f, так как он определяет потенциал точки f. Потенциал точки d выше потенциала точки fна падение напряжения на сопротивлении r : 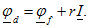Откладываем от конца вектора 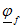вектор rI. Конец вектора rI обозначим буквой d, так как он определяет потенциал точки d. Действительно, если провести вектор из начала координат к концу вектора rl, то он будет равен сумме векторов 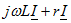, а эта сумма равна .

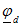12. Соединение обмоток генератора и приемников энергии звездой представляет собой схему, когда концы фаз соединяются в общий узел, а их начала присоединяются к линейным проводам