ФИЗИКО-ХИМИЧЕСКИЕ ЗАКОНОМЕРНОСТИ СТАЛЕПЛАВИЛЬНЫХ ПРОЦЕССОВ
Процессы производства стали представляют собой сложные комплексы физико-химических превращений, происходящих при высоких температурах. В процессах одновременно принимают участие многие компоненты, находящиеся в разных агрегатных состояниях: в твердом (футеровка плавильных агрегатов, добавки и т. п.), жидком (металл, шлак) и газообразном (атмосфера печи, продуваемый через металл воздух или кислород и т. п.).
В условиях непрерывного повышения требований к качеству металла, к уровню технико-экономических показателей того или иного процесса необходимо непрерывно углублять знания в области теории металлургических процессов. Достижения физической химии для усовершенствования металлургических процессов применяют начиная с 20—30-х годов XX в. Пионерами использования законов физической химии в металлургии в нашей стране были В. Е. Грум-Гржимайло, А. А. Байков, М. М. Карнаухов. Не только развитие и усовершенствование сталеплавильных процессов, но и обычное ведение плавки с целью получения стали нормального качества невозможны без использования основных положений физической химии. При изучении металлургии стали следует учитывать также тесную связь металлургии стали с химией, физикой, теплотехникой, металлографией и другими науками.
Физико-химические явления могут изучаться как опытным путем, путем непосредственного эксперимента, так и на основе выводов и обобщений теоретического характера и учета научных достижений в смежных областях знаний.
Существующие методы контроля обеспечивают получение информации о параметрах плавки стали (концентрации взаимодействующих веществ, давлении, температуре и т. д.). При совместном использовании полученной информации и законов физической химии определяют:
1) направление протекания процесса и продукты, которые должны образоваться в результате реакции;
2) конечное состояние системы, пределы, до которых может протекать процесс, состояние системы по окончании процесса;
3)скорость протекания процесса, ее зависимость от отдельных параметров.
Первые две задачи решаются методами термодинамики, третья — современными методами исследования кинетики процесса. Основные характеристики процесса (коэффициенты, параметры и т. п.), используемые при решении практических задач, часто получают экспериментально в лабораторных условиях. Однако результаты, полученные в лабораторных условиях (маленькие ванны, маленькие слитки и т. п.), не всегда соответствуют заводским данным. Для заводских условий характерно одновременное действие очень многих факторов, которые не всегда можно учесть в лабораторных установках. Чтобы получить наиболее достоверную информацию о процессе, требуется сочетание, по крайней мере, трех методов: расчетного, экспериментального и опытного.
8.1.1. Основные понятия физической химии, используемые при изучении металлургии стали.
Физическая химия как наука оперирует множеством терминов, понятий, имеющих оттенок специального научного значения. Приведем основные из них.
Система— группа тел, находящихся во взаимодействии и мысленно или физически выделенных из окружающей среды, например система металл-шлак, футеровка—металл и т. п. На практике чаще приходится иметь дело со сложной системой, например футеровка—металл—шлак—атмосфера агрегата, футеровка (свод)—металл—шлак-атмосфера агрегата—футеровка (под). Исследовать сложные системы трудно, поэтому для получения достаточно полного представления о процессах, происходящих в таких системах, обычно проводят исследования процессов, идущих в частных системах: металл-шлак, шлак—атмосфера и т. д., а затем, совмещая их, пытаются представить полную картину процесса в системе в целом. Такой метод не всегда оправдан, так как на практике процессы, протекающие в частных системах, идут одновременно и оказывают непрерывное взаимное влияние. Так, например, при продувке металла кислородом одновременно имеет место контакт газовой фазы и с металлом, и со шлаком, а также непосредственный контакт металла и шлака, шлака и футеровки и т. д.
В связи с этим результаты, полученные при исследовании процессов, протекающих в частных системах, распространять на всю систему нужно с большой осторожностью. В некоторой степени этим объясняется то, что, несмотря на обилие экспериментальных и теоретических работ по исследованию отдельных частных систем, многие вопросы, касающиеся объяснения процессов в реальных сложных системах, до сих пор до конца не ясны.
Гомогенная система1 — система, химический состав и физические свойства которой во всех частях одинаковы или меняются непрерывно, без скачков (между частями системы нет поверхностей раздела).
Гетерогенная система2 — физико-химическая система, состоящая из разных по своим свойствам частей, разграниченных поверхностями раздела.
При использовании понятий «металл», «шлак» и т. д. часто подразумевается, что эти части системы гомогенны, однако в большинстве случаев это не так. В металле содержатся неметаллические включения и пузыри газов, в шлаке — нерастворившиеся шлакообразующие, корольки металла, пузыри газов, в атмосфере — частички шлака (плавильная пыль), а иногда и металла.
Системы также могут быть однородными и неоднородными. Однородной называется система, в которой все участки объема имеют одинаковые состав (химически однородная) и свойства (физически однородная). В реальных сталеплавильных процессах как состав, так и свойства отдельных частей системы обычно очень неоднородны. Если, например, сделать мгновенный условный вертикальный разрез сталеплавильной печи (во время плавки), то выявится различие таких параметров, как: 1) химический состав подины, химический состав металлической ванны (по глубине), химический состав шлака (по толщине), состав атмосферы (по высоте), химический состав свода (по толщине кирпича); 2) температура (а соответственно и физические свойства) по толщине пода, глубине ванны, толщине шлака, высоте рабочего пространства, толщине свода. Даже в конвертере, несмотря на интенсивное перемешивание, свойственное этому процессу, состав всех частей системы неоднороден.
Фаза — совокупность всех гомогенных частей системы, отделенных от других частей системы поверхностью раздела и одинаковых по составу и свойствам. В металлургии имеют дело со следующими фазами: металл, шлак, атмосфера агрегата, дисперсная взвесь неметаллических включений в жидком металле и т. д. На практике фазой называют часть
1 Гомо (от греч. homoios) — подобный, одинаковый.
2Гетеро (от греч. heteros) —другой.
системы (металл, шлак и т. д.), не учитывая, что в действительности, например, металлическая фаза на самом деле является также системой, состоящей из нескольких фаз: жидкого металла, взвешенных твердых частиц, неметаллических материалов (футеровка, неметаллические включения), всплывающих жидких неметаллических включений. Из преведенного следует, что для практических целей допустимо условное использование терминов физхимии.
Параметры состояния —физические величины, служащие для характеристики состояния системы (давление, объем, концентрация компонентов, температура, плотность и др.).
Параметры процесса— величины, характеризующие процесс, т. е. изменение системы, связанное с изменением параметров состояния. Сталеплавильные процессы обычно протекают при практически постоянном давлении (р = const), т. е. являются изобарическим1, поэтому для термодинамических расчетов используют: величины изменения изобарно-изотермического потенциала ΔG, энтальпии2 ΔН, теплового эффекта при постоянном давлении Qp = - ΔН; соотношение между Qp и тепловым эффектом при постоянном объеме Qv имеет вид Qp= Qv-Δ( pV); если в реакции не принимают участие газообразные вещества, то различиями между Qp и Qv можно пренебречь. В настоящее время не существует методов определения абсолютного значения энтальпии Н. Для проведения термодинамических расчетов условились принимать энтальпию простых веществ (элементов) при 298,15 К (25 °С) равной нулю (Н298 = 0). При образовании из элементов каких-либо соединений определяют не абсолютные значения энтальпии Н, а ее изменение ΔН.
Энтропии всех веществ при абсолютном нуле принимают равными нулю (при Т= 0 и s0 = 0).
Схематически основные термодинамические функции можно представить в их взаимосвязи следующим образом:

Произведение TS часто называют связанной энергией; С—свободная энергия при постоянном давлении (кроме названия изобарно-изотерми-ческий потенциал в технической литературе можно встретить такие ее названия, как потенциал (или энергия) Гиббса2 , свободная энергия при постоянном давлении или просто свободная энергия). Чаще используются названия свободная энергия и изобарный потенциал. Из курса физической химии известно общее уравнение для определения изменения свободной энергии (или энергии Гиббса) при температуре Т:
Δ.GT= Δ.HT-T Δ ST.
Для проведения практических расчетов и сравнения получаемых результатов оказалось удобным определять изменения свободной энергии для каждого рассматриваемого процесса (реакции) при стандартных условиях. В качестве стандартных обычно принимают условия, при которых парциальное давление3 каждого компонента равно 100 кПа; активность каждого компонента равна единице; конденсированные вещества (жидкости и твердые тела) в жидком виде находятся также под давлением 100кПа. Чтобы показать, что параметры заданы для стандартных условий, используют индекс «°» (например, ΔG0 , Δ S°, ΔН°,). Стандартное изменение свободной энергии связано с константой равновесия реакции следующим образом:
Δ.G° = -RT ln Kp.
Это соотношение применимо для любой температуры. В качестве «стандартной» принимают обычно температуру 25 0С, или 298,15 К (в индексе указывают 298).
Итак, при стандартных условиях и стандартной температуре параметры процесса обозначают следующим образом: ΔН 0 298, Δ S 0 298 большинстве случаев температура металлургических процессов существенно отличается от стандартной, поэтому величины ΔН и ΔН 0 298 могут существенно различаться. Изменение ΔН в зависимости от температуры связано с изменением теплоемкости:
4 Энтальпия (теплосодержание) (от греч. enthalpo) — нагреваю.
5Тепловой эффект реакции — количество теплоты Q, выделяемой или поглощаемой системой при химической реакции, — равен изменению внутренней энергии системы при постоянном объеме или изменению ее энтальпии при постоянном давлении.
3 Изобарический (изобарный) процесс — термодинамический процесс, протекающий при постоянном давлении в системе. Изо... (от греч. was) —равный, одинаковый и бара (от греч. baros) —тяжесть.
1 Энтропия (от греч. entropid) — поворот, превращение.
2 По имени американского физика-теоретика D. Gibbs (1839—1903), одного из создателей термодинамики и статистической механики, разработавшего теорию термодинамических потенциалов.
3 100 кПа= 1 атм.
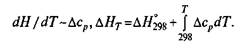
Если в пределах исследуемых температур происходит изменение состояния какого-либо компонента (аллотропическое превращение, плавление, испарение — обычно эти данные также приводятся в специальных таблицах), то тепловой эффект, связанный с этим изменением, (часто используют понятие теплота превращения Lnp или Qпр) должен быть учтен в расчетах:
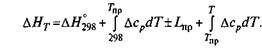
Величина изменения энтропии Δ S0 также зависит от температуры:
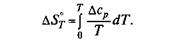
Если в рассматриваемом интервале температур имеет место какое-то превращение, то
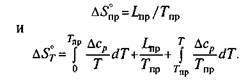
Если же никаких превращений в рассматриваемом интервале температур не происходит, то значение ΔG определяют при помощи выражения
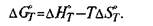
Для практических целей чаще используют таблицы, в которых приведены значения термодинамических функций при температурах сталеплавильных процессов, обычно при 1600 "С. На практике температурные условия процесса могут существенно отличаться от 1600 °С; это необходимо учитывать при количественной оценке того или иного процесса.
На практике чаще всего используют формулу
ΔG= ΔН-Т Δ S
где ΔН и Δ S близки к средним значениям ΔН и Δ S для данного интервала температур. В специальных таблицах значения приводят обычно в виде ΔG =А+ВТ(табл. 8.1).
Таблица 8.1.Стандартные энергии Гиббса
образования некоторых соединений при
температурах сталеплавильного производства
(1800-2000 К)
| Реакция | ДС" = A + ВТ, Дж | |
| A | В | |
| 2А1Ж + 1/2О2(г) = А12О3(тв) | -1676000 | 320,08 |
| Саг 1/2О2(г) = СаОтв | -186000 | 191,21 |
| Ств+ 1/2О2(г) = сог | -119700 | -83,05 |
| Ств + О2(г) = СО2(тв) | -396400 | 0,04 |
| 2Сеж+ 3/2О2(г)= Се203(тв) | -1826300 | 336,64 |
| Сеж + 02(г) = Се02(тв) | -1029300 | 214,22 |
| 2Сrтв + 3/202(г)=Сr203(тв) | -1132000 | 256,69 |
| 2Сuж + 1/2O2(г) = Cu2Oж | -146000 | 60,25 |
| Сuж+ 1/2О2(г) = СuОж | -154000 | 88,95 |
| H2(г)+ 1/2О2(г) = Н2Ог | -251500 | 57,91 |
| Feж+ 1/2О2(г) = FeОж | -257300 | 54,39 |
| 2Fеж + 1/2O2(г) = Fe2O3(тв) | -834300 | 260,20 |
| 3Fеж + 2O2(г) = Fe3O4(тв) | -1136800 | 324,43 |
| Mgг+1/2О2(г) = MgOтв | -729300 | 204,26 |
| Mnж+ 1/2О2(г) = MnОтв | -408000 | 88,78 |
| Мотв + О2(г) = МоО2(тв) | -437300 | 142,97 |
| 2Na+'/202(r) = Na2Oтв | -564000 | 266,90 |
| Niж + 1/2O2(г) = NiOтв | -252500 | 94,60 |
| Siж + 02(r) = Si02(ж) | -945800 | 197,36 |
| 2Tiтв + 3/2О2(г) = Ti2О3(тв) | -1480000 | 243,30 |
| Tiтв + О2(г) = TiО2 (тв) | -935500 | 176,11 |
| Wтв+ О2(r) = WO2(IB) | -564000 | 162,84 |
| Wтв+ 3/2О2(r) = WO3(IB) | -810000 | 230,12 |
| 2VTB + 3/2О2(r) = V2O3 (тв) | -1200000 | 225,94 |
| 2VTB + 5/2О2(r) = V2O5 (ж) | -1450000 | 317,27 |
| Zrтв + 02(r) =Zr02(тв) | -1084000 | 179,91 |
| Caж+1/2S2(г) = CaS (тв) | -702500 | 193,34 |
| Fеж+1/2S2(г) = FeSж | -125300 | 33,05 |
| Mgг+1/2S2(г) =MgSтв | -554600 | 197,65 |
| Мnж +1/2S2(г) = МnSж | -264000 | 65,98 |
| 1/2S2(г) + O2(r) = SO2(r) | -360700 | 72,26 |
При изменении температуры изменяются  и
и 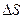 , но изменяется в большей мере; в результате оказывается, что
, но изменяется в большей мере; в результате оказывается, что 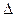 G
G 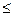 0. При р
0. При р  авновесии
авновесии 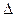 G = О, поэтому величина
G = О, поэтому величина 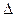 G для реакции, написанной в направлении ее протекания, всегда получается с минусом. Если в результате расчета величина
G для реакции, написанной в направлении ее протекания, всегда получается с минусом. Если в результате расчета величина 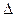 G получается положительной, то реакция (процесс) идет в обратном направлении. Процесс (реакция) развивается самопроизвольно лишь в том случае, когда энергия Гиббса системы уменьшается.
G получается положительной, то реакция (процесс) идет в обратном направлении. Процесс (реакция) развивается самопроизвольно лишь в том случае, когда энергия Гиббса системы уменьшается.
8.1.2. Растворы.В сталеплавильной ванне участвующие в реакциях компоненты находятся в виде раствора в металле (железе) и шлаке.
Раствором называют однородную смесь, состоящую из двух или большего числа веществ, состав которой в известных пределах может непрерывно изменяться (однородными являются и химические соединения, однако их состав не может изменяться непрерывно, так как они подчиняются законам постоянства состава и кратных отношений).
При рассмотрении растворов вообще и растворов, встречающихся в сталеплавильной практике, в частности следует учитывать химическое и физическое взаимодействия компонентов раствора. В одних случаях при образовании раствора никаких химических реакций не происходит, имеет место просто разбавление одного компонента другим; в других случаях одновременно с разбавлением происходит химическое взаимодействие растворителя и растворенного вещества. При этом выделяется (или поглощается) тепло, что важно учитывать на практике. Например, при образовании раствора кремния в железе выделяется значительное количество тепла. Это учитывается, например, при производстве кремнистой стали (динамной, трансформаторной, ЗОХГС и т. п.). Плавку можно организовать таким образом, что перед выпуском металла богатые кремнием ферросплавы в твердом виде можно загружать в ковш без опасения переохлаждения плавки.
Вещество, переходя в раствор, становясь компонентом раствора, теряет свою индивидуальность. Значение термодинамических функций для процессов (реакций), происходящих между веществами, находящимися в растворе, существенно отличается от таковых для реакций между чистыми веществами. Например, значения Δ G° для реакции окисления углерода, растворенного в металле, кислородом, находящимся в газообразном состоянии, или кислородом, растворенным в металле, различны:
1/202 + [С] = СОГ,
Δ G° = -142 000 -40,79 Т;
[О] + [С] = СОГ, ΔG 0= -25 000 -37,9 Т.
Взаимодействие частиц растворителя и растворенного вещества может быть различным. Количественной характеристикой, учитывающей как концентрацию данного компонента в растворе, так и его взаимодействие с растворителем (или вообще с другими компонентами раствора), является величина, называемая активностью данного компонента в данном растворе. Смысл понятия активность может быть ясен из следующего. Между любой жидкостью и парами этой жидкости устанавливается определенное равновесие (зависящее от температуры). Если в жидкости растворить какой-то другой компонент, то давление пара этой жидкости изменится. Значение подобного изменения широко используют в термодинамических расчетах. Чтобы результаты расчетов можно было сравнивать, необходимо выбрать стандартное состояние, которое является единицей сравнения. В качестве стандартного состояния можно выбрать любое состояние вещества. Обычно в качестве стандартного состояния выбирают либо чистое вещество, либо его однопроцентный раствор.
Если р — давление пара компонента, находящегося в растворе, а р° — давление пара компонента в стандартном состоянии, то соотношение р/р° принято называть активностью данного компонента и обозначать а, или р/р° = а. Активность вещества в стандартном состоянии принимают равной единице.
Для термодинамических расчетов активность представляет собой вспомогательную расчетную величину, которая характеризует степень связанности молекул, атомов или ионов исследуемого компонента. При образовании данным компонентом в растворе каких-либо соединений его активность понижается и, наоборот, активность возрастает при уменьшении сил взаимодействия между частицами растворителя и растворенного вещества. Теоретически можно представить случай, когда взаимодействие частиц растворителя и растворенного вещества равно взаимодействию частиц растворителя или чистого растворенного вещества. В этом случае при уменьшении концентрации в растворе одного из этих двух компонентов давление пара этого компонента над раствором уменьшается пропорционально уменьшению его концентрации в растворе, т. е. р = р°х, где х — мольная или атомная доля данного вещества в растворе. Это соотношение известно как закон Рауля, согласно которому давление пара каждого из компонентов раствора прямо пропорционально мольной доле данного компонента. В рассматриваемом случае (р = р°х; а = х) активность численно равна мольной доле компонента. Такой раствор принято называть идеальным.
Для реальных растворов закон Рауля не всегда соблюдается. Наблюдаемые отклонения от закона Рауля помогают установить природу образования тех или иных растворов. Представим себе раствор, состоящий из компонентов А и В. Частицы А и Л каким-то образом взаимодействуют между собой. Можно принять, что имеются какие-то силы FA.A взаимодействия частиц .А между собой, силы FB.B взаимодействия частиц В между собой и силы FA.B взаимодействия частиц А и В.
При этом возможны следующие случаи.
1. Силы взаимодействия частиц А и В равны: FA.A = FA_B = FB.B. В этом случае активности компонентов А и В равны их мольной доле (активности изменяются по мере разбавления раствора): аА = хА и ав = хв. Это идеальный раствор.
2. Силы взаимодействия между частицами Аи В меньше сил взаимодействия между частицами А—А и В—В, т. е. FA.A > FA.B < FB.B, ассоциированные молекулы А—В разъединяются; число молекул (частиц, комплексов) в растворе становится больше их числа в чистых компонентах. Практически наблюдается расширение системы (Δ V > 0), а также поглощение теплоты (  >0), которая затрачивается на разъединение ассоциированных молекул в чистых компонентах. Вследствие увеличения числа частиц в растворе парциальные давления и общее давление пара больше, чем в случае рА =р°АхА ир = рА + рв. Это положительное отклонение от закона Рауля.
>0), которая затрачивается на разъединение ассоциированных молекул в чистых компонентах. Вследствие увеличения числа частиц в растворе парциальные давления и общее давление пара больше, чем в случае рА =р°АхА ир = рА + рв. Это положительное отклонение от закона Рауля.
3. FA_A < FA_B > FB_B, т. е. различные молекулы стремятся ко взаимодействию типа притяжения (комплексо-образование, образование диполей и т. п.). В этом случае образование раствора сопровождается выделением теплоты (ΔН<0) и уменьшением объема (Δ V<0). Уменьшение числа частиц в растворе по сравнению с их числом в чистых растворителях приводит к уменьшению парциальных давлений пара компонентов и общего давления пара системы. Это отрицательное отклонение от закона Рауля. Характерным примером отрицательного отклонения от закона Рауля может служить раствор кремния в железе (рис. 8.1, а). Вид экспериментально полученной кривой свидетельствует о том, что силы взаимодействия кремния с железом FSi.Fe много больше сил .Fsi_si и FFe-Fe. , т.е. FSi-Si « FSi-Fe »FFe-Fe-
Отрицательным отклонением от закона Рауля характеризуются также растворы в железе таких компонентов, как алюминий, ванадий, титан. Если рассмотреть диаграммы состояния этих сплавов, то окажется, что в этих сплавах при охлаждении образуются химические соединения
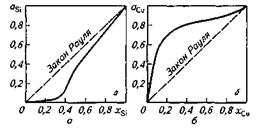
Рис. 8.1.Активность при 1873 К кремния (а) и меди (б) в жидких сплавах с железом
железа и растворенного компонента. Однако часто нас интересует не столько характер этих связей, сколько сам факт того, что какие-то связи имеются, значит, активность данного компонента в результате наличия этих связей уменьшается.
Примером положительного отклонения от закона Рауля (тенденция к отталкиванию молекул растворенного компонента) может служить раствор меди в железе (рис. 8.1, б). При сильных положительных отклонениях от закона Рауля наблюдается расслоение на две несмешивающиеся жидкости (системы Fe-Ag, Fe-Pb), что также приходится учитывать на практике. Например, для улучшения обрабатываемости, полируемости и других свойств некоторых стальных изделий в сталь необходимо вводить свинец. В связи с трудностью образования однородного раствора свинца в железе применяют специальные, иногда дорогостоящие технологические приемы и получают сталь, содержащую необходимое количество равномерно распределенного по массе металла свинца.
На практике чаще приходится иметь дело со сложными растворами (например, в железе одновременно растворены и кремний, и марганец, и углерод и т. д.). Влияние «третьего» компонента может быть различным. Так, например, такие примеси, как марганец или хром, образуют с железом раствор, близкий к идеальному; если же в железе имеется растворенный углерод, то при растворении марганца или хрома имело место отрицательное отклонение от закона Рауля.
Большинство компонентов, встречающихся в металлургической практике, образует с железом растворы, далекие от идеальных. Соотношения между составом и свойствами большинства реальных растворов очень сложны и не всегда ясны. Положение облегчается тем, что обычно технологи имеют дело с растворами, содержащими небольшие количества (часто < 1 %) других компонентов. При уменьшении концентрации растворенного вещества свойства реального раствора приближаются к свойствам идеального. Такие растворы принято называть бесконечно разбавленными или просто разбавленными. В этих случаях принято использовать закон Генри, согласно которому в разбавленном растворе давление пара растворенного вещества pj прямо пропорционально его концентрации Сj, т.е. pj = rCj, где r—коэффициент (константа Генри). Обычно реальные растворы подчиняются закону Генри при изменении концентрации в интервале от долей процента до нескольких процентов1.
Для достаточно сильно разбавленного раствора можно принять активность равной концентрации: aj= Сj, или aj — Xj. При повышении концентрации растворенного компонента приходится вводить вспомогательную величину аj =  jXj. Величина
jXj. Величина  j, называемая коэффициентом активности, характеризует степень отклонения свойств рассматриваемого компонента в данном растворе от его свойств в идеальном растворе. Для идеальных растворов
j, называемая коэффициентом активности, характеризует степень отклонения свойств рассматриваемого компонента в данном растворе от его свойств в идеальном растворе. Для идеальных растворов  = 1. К таким растворам близки растворы никеля, кобальта, марганца, хрома, молибдена в железе.
= 1. К таким растворам близки растворы никеля, кобальта, марганца, хрома, молибдена в железе.
Для ряда компонентов процесс растворения в железе сопровождается выделением (или поглощением) тепла (ΔН #0), а энтропия при растворении изменяется так же, как и в идеальных растворах, — только вследствие изменения концентрации Δ S° = — Rlnx. Это справедливо для растворов кремния, алюминия, меди в железе (такие растворы иногда называют регулярными). Для многих растворов приходится учитывать изменение энтропии не только в зависимости от концентрации, но и вследствие взаимодействия вещества с растворителем Δ S°=—Rlnx+ Δ S 0 вз.
К ним относятся, например, растворы в железе углерода, серы (подобные растворы иногда называют реальными). Уравнения изменения энергии Гиббса при растворении ряда элементов в жидкой стали в числовом виде приведены в табл. 8.2. Для обозначения коэффициентов активности обычно используют символ  или f. Буквой у обозначают коэффициент активности при использовании соотношения aj=
или f. Буквой у обозначают коэффициент активности при использовании соотношения aj=  jxj, т. е. когда концентрация выражена в мольных долях (компонента j). При выражении массовой концентрации в процентах для обозначения чаще используют букву f. В реальных условиях величина коэффициента активности компонента в растворе зависит от взаимодействия растворенных в металле других компонентов. Для определения характера изменения коэффициента активности при изменении концентрации компонентов расплава обычно используют соотношения, предложенные К. Вагнером. Если за стандартное состояние принят чистый компонент i, то при наличии в растворе кроме i других компонентов с мольными долями a, b, ...,j
jxj, т. е. когда концентрация выражена в мольных долях (компонента j). При выражении массовой концентрации в процентах для обозначения чаще используют букву f. В реальных условиях величина коэффициента активности компонента в растворе зависит от взаимодействия растворенных в металле других компонентов. Для определения характера изменения коэффициента активности при изменении концентрации компонентов расплава обычно используют соотношения, предложенные К. Вагнером. Если за стандартное состояние принят чистый компонент i, то при наличии в растворе кроме i других компонентов с мольными долями a, b, ...,j
Inyi =ln  0 i +
0 i + 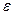 ii
ii 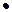 i+
i+ 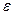 ai
ai 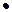 а+
а+ 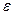 bi
bi 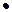 Ь+...+
Ь+...+ 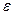 ji
ji 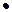 j,
j,
где 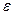 ii,
ii, 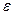 ai,
ai, 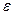 bi,...
bi,... 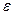 ji, —параметры взаимодействия;
ji, —параметры взаимодействия;
Таблица 8.2.Изменение энергии Гиббса
при образовании 1%-ного раствора ряда
элементов в жидком железе
| Растворенный элемент | Yl873K | ДС° = ДД° - | ГдУ, Дж |
| А1 | 0,049 | -62800 - | 23,85 Т |
| В | 0,040 | -73200 - | 12,30 Т |
| С | 0,57 | 22600 - | 42,26 Т |
| Са | 16200 - | 58,58 Т | |
| Со | 1,07 | 1400 - | 38,91 Т |
| Сг | 1,0 | — | 37,66 Т |
| Сu | 8,6 | 47200 - | 46,65 Т |
| 1/2H2(г) Мn | 1,3 | 36500 + 5500 - | 30,46 Т 39,12 Т |
| Мо | 1,0 | - | 42,80 Т |
| 1/2N2(r) Ni | 0,66 | 10500 + -18000 - | 20,38 Т 32,63 Т |
| 1/2O2(г) 1/2P2 Pb | -117000 - -140200 -212500 - | 2,89 Т 9,62 Т 106,27 Т | |
| 1/2S2(r) Si | 0,0013 | -72000 – -131800 - | 10,25 Т 17,32 Т |
| Ti | 0,037 | -69500 - | 27,28 Т |
| V | 0,18 | -42300 - | 29,20 Т |
| W | 1,0 | — | 48,12 Т |
| Zr | 0,022 | -80300 - | 31,38 Т |
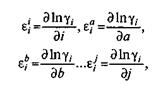
т. е. параметр взаимодействия 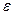 ii показывает, как изменяется коэффициент активности
ii показывает, как изменяется коэффициент активности  I при изменении мольной доли i; параметр
I при изменении мольной доли i; параметр 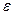 ai — как изменяется
ai — как изменяется  I при изменении мольной доли компонента а и т. д. Для удобства расчетов параметры взаимодействия чаще определяют, принимая за стандартное состояние 1%-ный (по массе) идеальный разбавленный раствор компонента i. В этом случае параметр взаимодействия обозначают буквой е (а коэффициент активности — буквой f):
I при изменении мольной доли компонента а и т. д. Для удобства расчетов параметры взаимодействия чаще определяют, принимая за стандартное состояние 1%-ный (по массе) идеальный разбавленный раствор компонента i. В этом случае параметр взаимодействия обозначают буквой е (а коэффициент активности — буквой f):

Если компонент а увеличивает величину fi, этому соответствует 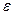 ai>0 (т. е. параметр взаимодействия имеет знак «плюс»). Если компонент Ь уменьшает fi этому соответствует еbi <0 (т. е. параметр взаимодействия имеет знак «минус»). Это означает, что компонент а взаимодействует с железом сильнее, чем компонент i, а компонент b слабее. Значения некоторых параметров взаимодействия приведены в табл. 8.3.
ai>0 (т. е. параметр взаимодействия имеет знак «плюс»). Если компонент Ь уменьшает fi этому соответствует еbi <0 (т. е. параметр взаимодействия имеет знак «минус»). Это означает, что компонент а взаимодействует с железом сильнее, чем компонент i, а компонент b слабее. Значения некоторых параметров взаимодействия приведены в табл. 8.3.
Таблица 8.3.Параметры взаимодействия 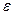 ii
ii 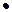 100 в железе при 1873 К
100 в железе при 1873 К
| Элемен i | Элемент j | |||||||||||
| Al | С | Сг | Си | Мп | Н | |||||||
| А1 | 4,5 | 9,1 | — | _ | — | |||||||
| С | 4,3 | -2,4 | 1,6 | -1,2 | ||||||||
| Сг | — | -12 | -0,03 | 1,6 | — | -33 | ||||||
| Си | _ | 6,6 | 1,8 | 2,3 | — | -24 | ||||||
| Мп | — | -7 | — | — | -31 | |||||||
| Н | 1,3 | -0,22 | 0,05 | -0,14 | ||||||||
| N | -2,8 | -4,7 | 0,9 | _2 | — | |||||||
| -390 | -45 | -4 | -1,3 | -2,1 | -310 | |||||||
| Ni | — | 4,2 | -0,03 | — | — | -25 | ||||||
| Р | — | _з | 2,4 | |||||||||
| S | 3,5 | -1,1 | -0,84 | -2,6 | ||||||||
| Si | 5,8 | -0,03 | 1,4 | 0,2 | ||||||||
| А1 | -5,8 | -660 | — | — | 0,56 | |||||||
| С | -34 | 1,2 | 5,1 | 4,6 | ||||||||
| Сг | -19 | -14 | 0,02 | -5,3 | -2 | -0,43 | ||||||
| Си | 2,6 | -6,5 | — | 4,4 | -2,1 | 2,7 | ||||||
| Мп | -9,1 | -8,3 | — | -0,35 | -4,8 | |||||||
| н | — | -19 | 1,1 | 0,8 | 2,7 | |||||||
| N | 4,5 | 0,7 | 4,7 | |||||||||
| О | 5,7 | -20 | 0,6 | -13,3 | -13,1 | |||||||
| Ni | 2,8 | 0,09 | -0,35 | -0,37 | 0,57 | |||||||
| Р | 9,4 | 0,02 | 6,2 | 2,8 | ||||||||
| S | -27 | -2,8 | 6,3 | |||||||||
| Si | -23 | 0,5 | 5,6 | |||||||||
8.1.3. Химическое сродство. Способность веществ вступать в химическое взаимодействие называют химическим сродством. Изменение энергии Гиббса используют для определения меры химического сродства веществ. Константа равновесия Кр характеризует степень протекания реакции в ту или иную сторону. Поскольку Δ G° =  o -T
o -T 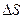 ° и Δ G° = -RTlnKp, то -RT\nKp = kH°-TAS°, откуда RlnKp =
° и Δ G° = -RTlnKp, то -RT\nKp = kH°-TAS°, откуда RlnKp = 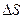 о —
о —  °/Т. Отсюда видно, что чем больше величина
°/Т. Отсюда видно, что чем больше величина 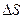 ° и чем меньше
° и чем меньше  °/Т, тем полнее идет реакция. Из уравнения видно также, что чем выше температура, тем большее значение имеет величина
°/Т, тем полнее идет реакция. Из уравнения видно также, что чем выше температура, тем большее значение имеет величина 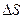 ° (энтропийный фактор) и меньшее
° (энтропийный фактор) и меньшее  °/Т(энтальпийный фактор).
°/Т(энтальпийный фактор).
При производстве стали протекают процессы окисления железа и его примесей (углерода, кремния, марганца) с образованием соответствующих оксидов (СО, SiO2, MnO). Способность железа и его примесей окисляться, т. е. химическое сродство к кислороду, часто выражают при помощи давления диссоциации оксидов. Давление диссоциации1 в данном случае представляет собой давление кислорода РО2 при равновесии системы кислород—оксид:
Me + О2 = МеО2,
Kp = aMeO2 /(aMe 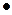 Pо2 )
Pо2 )
.
В случае чистых металла и оксида а Mе02=l и аМе= 1,т. е.
Кр=1/р О2 и ΔG º=RТlnPo2.
Таким образом, давление диссоциации является мерой прочности оксида: чем меньше эта величина, тем прочнее оксид. Процессы окисления примесей в сталеплавильной ванне с использованием понятия давления диссоциации их оксидов исследованы акад. М. М. Карнауховым. Вычисленные им давления диссоциации оксидов в зависимости от изменения температуры при различных концентрациях того или иного компонента широко используют в металлургической литературе. Если металлы и их оксиды находятся в растворе, а не в свободном состоянии, то давление диссоциации зависит от активности растворенных веществ:
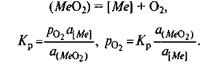
Если металл и его оксид находятся в стандартном состоянии, т. е. активности их могут быть приняты равными единице, то ро2=Кp = рo. Таким образом, в общем случае

т. е. давление диссоциации прямо пропорционально активности данного оксида в растворе и обратно пропорционально активности растворенного компонента.
Дата добавления: 2016-01-29; просмотров: 764;
