Коэффициент безопасности
Коэффициентом безопасности называют отношение предельных напряжений к максимальным напряжениям, возникающим при работе детали.
1. Коэффициент безопасности при статических нагрузках можно определять по формулам:
для пластичных материалов
 (1.10)
(1.10)
для хрупких материалов
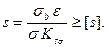 (1.11)
(1.11)
2. Коэффициент безопасности при переменных (циклических) нагрузках с учетом основных факторов, влияющих на предел выносливости, для любого материала определяют [15; 35; 5] по формулам:
при симметричном цикле
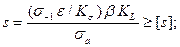 (1.12)
(1.12)
при асимметричном цикле, когда с возрастанием нагрузки цикл остается подобным рабочему [14; 5], т. е. возрастание напряжений происходит по направлению ОМN (рис. 1.3):

Рис. 1.7. Диаграмма предельных напряжений
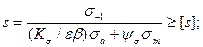 (1.13)
(1.13)
при асимметричном цикле, когда среднее напряжение не меняется, а амплитуда растет, т. е. по линии МР (рис. 1.3):
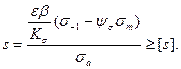 (1.14)
(1.14)
При совместном действии нормального σа и касательного τа напряжений (изгиб, кручение), изменяющихся синфазно,
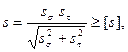 (1.15)
(1.15)
где sσ; sτ – коэффициент безопасности по нормальным и касательным напряжениям (1.24. . .1.26) с заменой σ на τ.
Допустимое значение коэффициента безопасности [s] назначают на основании опыта проектирования и эксплуатации машин или рассчитывают с учетом требуемой надежности деталей. При отсутствии необходимых данных допустимый коэффициент безопасности приближенно можно определить на основе так называемого дифференциального метода как произведение частных коэффициентов [14; 38]:
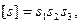 (1.16)
(1.16)
где s1 – коэффициент, учитывающий степень точности расчета. Расчет приводить к завышенным напряжениям и степень завышения определить трудно: s1 = 1, расчет приводит к заведомо заниженным напряжениям; s1 = 1,2...1,3; s2 – коэффициент, учитывающий однородность механических свойств материала. Для деталей, изготовленных из углеродистых и легированных сталей при высокой температуре отпуска, s2 = 1,2...1,3; для деталей, изготовленных из высокопрочных сталей с пониженными пластическими свойствами (с низкой температурой отпуска) и высокопрочных чугунов, s2 = 1,3...1,5; для деталей из стального литья s2 = 1,5...2; для чугунных деталей s2 = 2...2,5; для деталей из цветных сплавов (кованых и катаных) s2 = 1,5...2; s3 – коэффициент, учитывающий степень ответственности детали. Поломка детали не вызывает остановки машины: s3 = 1; поломка детали вызывает остановку машины: s3 = 1,1...1,2; поломка детали вызывает аварию: s3 = 1,2…1,3.
Коэффициент безопасности по пределу прочности выбирается довольно большим. Например, для высокопрочных сталей – около 2...2,5, для серого чугуна 3...3,5, для стального и цветного литья 2,5...3, для особо хрупких материалов 4...6.
Коэффициент безопасности по пределу текучести для пластичных материалов (сталей) при достаточно точных расчетах выбирают 1,2...1,5 и выше. Коэффициент безопасности при контактных нагружениях можно принять 1,1...1,2. Коэффициент безопасности по пределу выносливости – 1,3...2,5. Например, при недостаточно полном объеме экспериментальных данных о нагрузках и характеристиках материала или ограниченном числе натурных испытаний [s] = 1,5...2; при малом объеме или отсутствии экспериментальных испытаний и пониженной однородности материала (литые и сварные детали) [s] = 2...3.
Пример. Определить коэффициент безопасности для вала d = 60 мм с одной шпоночной канавкой, который нагружен в опасном сечении изгибающим моментом М = 1,5 · 106 Н · мм и крутящим моментом Т = 4 · 106 Н · мм. Материал вала – сталь 40ХН (табл. 1.2, σb = 1000 Н/мм2; σ-1F = 530 Н/мм2). Поверхность вала шлифованная. Напряжение изгиба изменяется по симметричному циклу, кручения – по пульсирующему. Срок службы NLE > N0
Решение.
1. При сложном напряженном состоянии (изгиб и кручение) коэффициент безопасности определяется по выражению (1.15)

где sσ, sτ– коэффициент безопасности по изгибу и кручению.
2. По формуле определяем коэффициент безопасности по нормальным напряжениям при симметричном цикле изгиба:
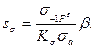
Здесь амплитудное и наибольшее напряжения цикла равны и определяются по формуле:
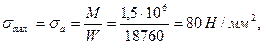
где W = 18 760 мм3 – момент сопротивления изгибу вала d = 60 мм, ослабленного шпоночным пазом.
3. Находим эффективный коэффициент концентрации напряжений для валов с одной шпоночной канавкой при изгибе (σb = 1000 Н/мм ) Кσ = 2,3; масштабный фактор ε = 0,77; коэффициент состояния поверхности β = 0,88.
Тогда
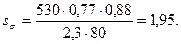
4. Коэффициент безопасности по касательным напряжениям при пульсирующем цикле нагружения по формуле:

5. По выражению определим амплитудное и среднее напряжения:
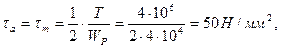
где Wр = 4 · 104 мм3 — момент сопротивления кручению вала ослабленного шпоночным пазом.
6. Находим масштабный фактор ε = 0,77; коэффициент состояния поверхности β = 0,88; коэффициент чувствительности материала к асимметрии ψτ = 0,09.
Эффективный коэффициент концентрации напряжений при кручении Kτ = 2,2.
7. Используя приближенное соотношение

Определяем τ-1 = 0,55 · 530 = 290 Н/мм2.
Тогда
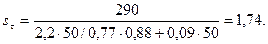
8. Определяем коэффициент безопасности
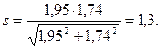
Для выяснения прочности вала установим минимально допустимый коэффициент безопасности по выражению (1.16):
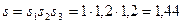
где s1 = 1; s 2 = 1,2; s3 = 1,2 (с. 16).
 Таким образом, s<[s] и, следовательно, прочность вала недостаточна. Необходимо принять решение к повышению s.
Таким образом, s<[s] и, следовательно, прочность вала недостаточна. Необходимо принять решение к повышению s.
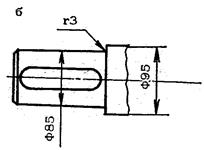
Рис. 1.8. Эскиз к примеру 1
Соединения
Дата добавления: 2016-01-29; просмотров: 3201;
