ДВИЖЕНИЕ КАК ВЗАИМООТНОШЕНИЕ

Вывод Галилея о том, что состояния покоя и равномерного движения эквивалентны и взаимозаменяемы, означал, что они являются относительными. Так он открыл дорогу новой относительной теории движения, противопоставленной аристотелевскому представлению о движении как о внутренней тенденции. Начиная с Галилея движение стали рассматривать как взаимоотношение тел. Так он писал в своих «Диалогах...»:

«Движение является движением и воздействует как таковое, поскольку оно имеет отношение к вещам, его лишенным, но на вещи, которые равным образом участвуют в этом движении, оно не воздействует совсем как если бы его не было. [...] Итак, очевидно, что движение, общее для многих движущихся тел, как бы не существует, если речь идет об отношении движущихся тел друг к другу (раз среди них ничто не меняется), и проявляется только в изменении отношения этих движущихся тел к другим, не обладающим таким движением (ибо здесь меняется их взаимное расположение) [...]».

Там, где он говорит об «общем движении», мы бы сказали «общая система отсчета». Так, Галилей утверждает, что когда разные тела находятся внутри единой системы отсчета, которая, в свою очередь, пребывает в состоянии движения, то его скорость должна считаться чем‑то «несуществующим».

В качестве дополнения к предыдущему постулату мы должны сказать, что не всегда у движения есть источник или причина, как считал Аристотель. В случае равномерного движения его причины неважны и ими можно пренебречь. Больше не нужно было прибегать к странным теориям о слоях воздуха, работающим как источник; в действительности объяснять было нечего.

ИНЕРЦИЯ

Как мы увидели, Галилей использовал понятие инерции, чтобы атаковать теорию Аристотеля и расчистить место для нового представления о пространстве. Однако ему не удалось отделаться от всех ошибочных идей, поэтому при формулировке принципа инерции, хотя взгляды исследователя и были верными, он допустил грубейшую ошибку.

В его сочинениях, главным образом в «Беседах...», мы находим некоторые интеллектуальные эксперименты, которые и сегодня являются интереснейшим введением к пониманию этого принципа. В первом примере Галилей описывает следующую ситуацию: на наклонной поверхности, гладкой настолько, что можно не принимать в расчет ее сопротивление, лежит бронзовый шар. Если мы отпустим его, он будет скользить, равномерно ускоряясь. Теперь расположим поверхность горизонтально и поместим шар на ее край. Слегка толкнув шар, спросим себя: «Какое расстояние пройдет движущееся тело?» Поскольку нет ни сопротивления, ни чего‑либо другого, что тормозит предмет, его скорость будет постоянной. Как говорит Сальвиати, «если бы это расстояние было бесконечным, то и тело двигалось бы без конца, то есть вечно».

ИНЕРЦИЯ В ДИАЛОГЕ...»

Галилей неоднократно упоминает принцип инерции в своем «Диалоге...» (хотя и не называет его принципом), например в следующем отрывке:

Сальвиати: ...если у вас имеется плоская поверхность, совершенно гладкая, как зеркало, из вещества твердого, как сталь, не параллельная горизонту, но несколько наклонная, и если вы положите на нее совершенно круглый шар из вещества тяжелого и весьма твердого, например из бронзы, то что, думаете вы, он станет делать, будучи предоставлен самому себе? Не думаете ли вы (как я думаю), что он будет неподвижным?

Симпличио: ...шар продолжал бы катиться до бесконечности, лишь бы продолжалась такая плоскость, и притом движением непрерывно ускоряющимся, ибо такова природа тяжелых перемещающихся тел, которые vires acuirant eundo (движение приобретают в пути), и чем больше будет наклон, тем больше будет и скорость.

Сальвиати: ...что произошло бы с тем же движущимся телом на поверхности, которая не поднимается и не опускается?

Симпличио: Здесь мне нужно немного подумать над ответом. Раз там нет наклона, то не может быть естественной склонности к движению, и раз там нет подъема, не может быть противодействия движению, так что тело [...] должно оставаться неподвижным.

Сальвиати: Так, думаю я, если бы шар положить неподвижно; но если придать ему импульс движения в каком‑нибудь направлении, то что воспоследовало бы?

Симпличио: Воспоследовало бы его движение в этом направлении.

Сальвиати: Но какого рода было бы это движение: непрерывно ускоряющееся, как на плоскости наклонной, или постепенно замедляющееся, как на плоскости поднимающейся?

Симпличио: Я не могу открыть здесь причины для ускорения или для замедления, поскольку тут нет ни наклона, ни подъема.

Сальвиати: Так, но если здесь нет причины для замедления, то тем менее может находиться здесь причина для покоя. Поэтому сколь долго, полагаете вы, продолжалось бы движение этого тела?

Симпличио: Столь долго, сколь велика длина такой поверхности без спуска и подъема.

Сальвиати: Следовательно, если бы такое пространство было беспредельно, движение по нему равным образом не имело бы предела, то есть было бы постоянным?

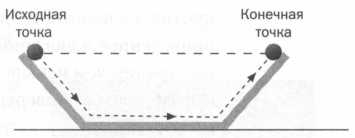
РИС.З

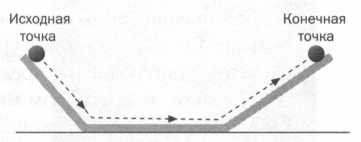
РИС. 4

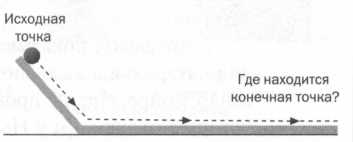
РИС. 5

Эксперимент, придуманный Галилеем для демонстрации принципа инерции: в отсутствие трения из‑за инерции движения шар будет продолжать перемещаться бесконечно, если плоскость, по которой он катится, абсолютно ровная.

В другом своем мысленном эксперименте Галилей приходит к таким же выводам, но еще более изобретательным путем.

Эксперимент состоял в том, чтобы представить себе поверхность настолько гладкую, что она не создает никакого сопротивления, разделенную на три части: одна наклонная, вторая горизонтальная и третья наклонная под таким же углом, но противоположная первой.

В первой фазе эксперимента (рис. 3) на край одной из плоскостей ставят шар, тоже настолько гладкий, что поверхность не оказывает никакого сопротивления.

Поскольку трение отсутствует, шар докатится до конца плоскости и поднимется по наклонной части до той же высоты, откуда он был брошен.

Теперь представим, что угол наклонной поднимающейся плоскости уменьшился (рис. 4). Мы снова запускаем шар с того же конца, и он опять поднимется до той же высоты, но теперь ему придется пройти большее расстояние. По мере того как третья плоскость опускается, шар будет проходить все большее расстояние, чтобы подняться до исходной высоты.

Что же произойдет, когда поверхность опустится на угол в 180° и станет горизонтальной (рис. 5)? В этом последнем из возможных вариантов расстояние, которое должен пройти шар, станет бесконечным. Это значит, что шар продолжит свой путь на постоянной скорости без остановки, бесконечно. Галилей пишет:

«Если большему наклону соответствует большая скорость, и, напротив, на плоскости, поднимающейся вверх, то же самое тело, приведенное в движение такой же силой, пройдет тем большее расстояние, чем меньше будет угол, то скажите мне, что случится с этим телом на поверхности, которая не будет ни подниматься, ни опускаться».

Несмотря на эти четкие объяснения и примеры, Галилей пришел к ошибочному выводу, что по принципу инерции тела бесконечно двигаются не по прямой линии, а по кругу. По мнению Галилея, было абсурдно предположить, что траектория вечно движущегося предмета может быть прямой. В шарообразном и замкнутом мире, каким продолжал представлять его Галилей (идея Джордано Бруно о бесконечной Вселенной не нашла отклика среди других мыслителей того времени), не было места для прямых бесконечных линий. Поэтому инерционное движение должно было происходить по круговой траектории.

Этот вывод показывает, что Галилей еще не четко разделял материю и пространство, то есть, как пишет историк Александр Койре, еще не произошла геометризация пространства, которую мы увидим у Ньютона. Наконец, круговое инерционное движение согласовывалось с движением планет (Галилей не знал о результатах Кеплера в этой области) и служило объяснением траектории движения планет вокруг Солнца.

Как бы там ни было, благодаря принципу инерции Галилей смог дать отпор критике идеи движения Земли со стороны последователей Аристотеля: поскольку мы сами являемся частью той же системы отсчета, что и Земля, то не видим признаков ее движения, потому что покой, который мы наблюдаем, есть не что иное, как «разделяемое движение». Все, кто участвует в движении Земли, не будут воспринимать его таковым; это движение будет невидимым и неосязаемым. С практической точки зрения находиться в состоянии покоя или равномерного движения – это одно и то же, и поэтому перипатетики не могут доказать неподвижность Земли, кидая с высоты камень.