Температурная зависимость электропроводности полупроводников
Закон Ома в дифференциальной форме
 (35.2)
(35.2)
содержит удельное сопротивление 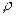 или удельную электропроводность
или удельную электропроводность 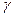 . Удельное сопротивление характеризует преобразование энергии электрического тока в теплоту. Плотность тока в металле
. Удельное сопротивление характеризует преобразование энергии электрического тока в теплоту. Плотность тока в металле
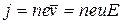 , (35.3)
, (35.3)
где 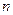 – концентрация электронов проводимости,
– концентрация электронов проводимости,  – элементарный заряд,
– элементарный заряд, 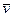 – средняя скорость направленного движения электронов,
– средняя скорость направленного движения электронов, 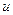 – подвижность электронов проводимости, равная средней скорости направленного движения, приобретаемой электронами под действием электрического поля единичной напряженности. Из (35.2) и (35.3) получаем
– подвижность электронов проводимости, равная средней скорости направленного движения, приобретаемой электронами под действием электрического поля единичной напряженности. Из (35.2) и (35.3) получаем
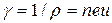 . (35.4)
. (35.4)
В металлах подвижность 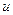 электронов с повышением температуры уменьшается, так как в результате возрастания амплитуды тепловых колебаний атомов электроны чаще с ними сталкиваются, а поэтому между столкновениями ускоряются внешним полем до меньших скоростей. Концентрация
электронов с повышением температуры уменьшается, так как в результате возрастания амплитуды тепловых колебаний атомов электроны чаще с ними сталкиваются, а поэтому между столкновениями ускоряются внешним полем до меньших скоростей. Концентрация 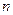 электронов проводимости в металлах от температуры не зависит. Поэтому с повышением температуры удельная электропроводность
электронов проводимости в металлах от температуры не зависит. Поэтому с повышением температуры удельная электропроводность 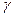 металлов уменьшается, а удельное сопротивление возрастает.
металлов уменьшается, а удельное сопротивление возрастает.
Удельную электропроводность чистого (беспримесного) полупроводника, называемая собственной удельной электропроводностью,
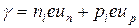 , (35.5)
, (35.5)
где 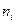 ,
,  – концентрации, а
– концентрации, а 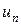 и
и 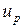 – подвижности электронов проводимости и дырок, соответственно.
– подвижности электронов проводимости и дырок, соответственно.
В беспримесных полупроводниках уровень Фéрми лежит приблизительно посередине запрещенной зоны. Поэтому для электронов зоны проводимости, располагающихся вблизи дна зоны проводимости, показатель степени в (35.1)
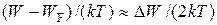 . (35.6)
. (35.6)
С учетом того, что 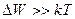 , вероятность заполнения электронами состояний зоны проводимости
, вероятность заполнения электронами состояний зоны проводимости
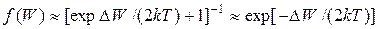 . (35.7)
. (35.7)
Количество электронов, перешедших в зону проводимости, а следовательно, и количество дырок, образовавшихся в валентной зоне, будет пропорционально вероятности (35.7).
В полупроводниках, так же как и в металлах, с повышением температуры подвижности электронов 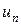 и дырок
и дырок 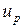 возрастают, но концентрация носителей вследствие перехода все новых электронов из валентной зоны в зону проводимости растет значительно быстрее. В результате удельная электропроводность полупроводника растет:
возрастают, но концентрация носителей вследствие перехода все новых электронов из валентной зоны в зону проводимости растет значительно быстрее. В результате удельная электропроводность полупроводника растет:
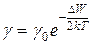 , (35.8)
, (35.8)
 где
где  – основание натуральных логарифмов,
– основание натуральных логарифмов, 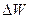 – ширина запрещенной зоны,
– ширина запрещенной зоны, 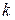 – постоянная Больцмана,
– постоянная Больцмана, 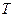 – абсолютная температура,
– абсолютная температура, 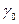 – предельное значение удельной электропроводности полупроводника при устремлении температуры в бесконечность, когда населенности валентной зоны и зоны проводимости электронами практически выравнивается. Таким образом, удельная электропроводность полупроводника с повышением температуры возрастает по экспоненциальному закону (см. рис. 35.10).
– предельное значение удельной электропроводности полупроводника при устремлении температуры в бесконечность, когда населенности валентной зоны и зоны проводимости электронами практически выравнивается. Таким образом, удельная электропроводность полупроводника с повышением температуры возрастает по экспоненциальному закону (см. рис. 35.10).
Температурная зависимость сопротивления полупроводника имеет вид:
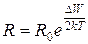 , (35.9)
, (35.9)
где 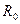 – предельное значение сопротивления полупроводника при устремлении температуры в бесконечность. При низких температурах удельное сопротивление полупроводника весьма велико и он практически является изолятором, а при очень высоких температурах удельное сопротивление становится почти таким же, как у металлов.
– предельное значение сопротивления полупроводника при устремлении температуры в бесконечность. При низких температурах удельное сопротивление полупроводника весьма велико и он практически является изолятором, а при очень высоких температурах удельное сопротивление становится почти таким же, как у металлов.
К полупроводникам принадлежат кристаллы многих элементов таблицы Менделеева (кремний Si, германий Ge, селен Se и др.), закись меди 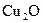 , сернистый свинец
, сернистый свинец 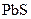 и многие другие химические элементы. Современна микроэлектроника практически полностью базируется на кремнии. Атом кремния имеет порядковый номер в периодической системе Менделеева
и многие другие химические элементы. Современна микроэлектроника практически полностью базируется на кремнии. Атом кремния имеет порядковый номер в периодической системе Менделеева 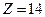 . Поэтому заряд ядра атома кремния равняется
. Поэтому заряд ядра атома кремния равняется 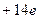 и в состав атома входит 14 электронов. Четыре из них образуют наиболее удаленную от ядра электронную
и в состав атома входит 14 электронов. Четыре из них образуют наиболее удаленную от ядра электронную  оболочку. Эти четыре электрона сравнительно слабо связаны с ядром. Они обеспечивают четыре ковалентные связи кремния в химических соединениях и поэтому называются валентными электронами. Остальные десять электронов вместе с ядром образуют остов атома, имеющий заряд
оболочку. Эти четыре электрона сравнительно слабо связаны с ядром. Они обеспечивают четыре ковалентные связи кремния в химических соединениях и поэтому называются валентными электронами. Остальные десять электронов вместе с ядром образуют остов атома, имеющий заряд  . Четыре валентных электрона движутся вокруг остова и образуют облако отрицательного заряда. На рис. 35.11 показано схематическое изображение атома кремния с его четырьмя ковалентными связями.
. Четыре валентных электрона движутся вокруг остова и образуют облако отрицательного заряда. На рис. 35.11 показано схематическое изображение атома кремния с его четырьмя ковалентными связями.
 В кристаллической решетке кремния каждый атом окружен четырьмя ближайшими соседями. Упрощенная плоская схема размещения атомов изображена на рис. 35.12. Связь двух соседних атомов осуществляется парой электронов, обеспечивающих так называемую парно-электронную, или ковалентную связь. Изображенная картина соответствует чистому кремнию при очень низкой температуре. В этом случае все валентные электроны задействованы в образовании связей между атомами и не могут принимать участие в электропроводности.
В кристаллической решетке кремния каждый атом окружен четырьмя ближайшими соседями. Упрощенная плоская схема размещения атомов изображена на рис. 35.12. Связь двух соседних атомов осуществляется парой электронов, обеспечивающих так называемую парно-электронную, или ковалентную связь. Изображенная картина соответствует чистому кремнию при очень низкой температуре. В этом случае все валентные электроны задействованы в образовании связей между атомами и не могут принимать участие в электропроводности.
 При повышении температуры кристалла тепловые колебания решетки приводят к разрыву некоторых ковалентных связей. Вследствие этого часть электронов, задействованных ранее в образовании ковалентных связей, отщепляются и становятся электронами проводимости. При наличии внешнего электрического поля они перемещаются против поля и создают электрический ток.
При повышении температуры кристалла тепловые колебания решетки приводят к разрыву некоторых ковалентных связей. Вследствие этого часть электронов, задействованных ранее в образовании ковалентных связей, отщепляются и становятся электронами проводимости. При наличии внешнего электрического поля они перемещаются против поля и создают электрический ток.
Уход электрона, ранее принимавшего участие в образовании ковалентной связи, приводит к появлению вакансии – “дырки” (см. рис. 35.13). Возникновение дырок создает дополнительную возможность для перенесения заряда. Действительно, при наличии дырки валентный электрон соседнего атома под действием внешнего электрического поля может перейти на место дырки. Тогда в этом месте восстановится ковалентная связь, но зато возникнет дырка в позиции, из которой перешел валентный электрон, заполнивший вакансию. В эту новую дырку сможет перейти валентный электрон из другого соседнего атома и т. д. Вследствие этого ток будет поддерживаться не только электронами проводимости, но и валентными электронами, которые перемещаться точно так же, как и электроны проводимости, против электрического поля. Дырки же будут перемещаться в направлении электрического поля, то есть так, как двигались бы положительно заряженные частицы. Таким образом, в полупроводниках возможны два типа электропроводности: электронный, осуществляемый движением электронов проводимости, и дырочный, обусловленный движением дырок.
Наряду с переходами электронов из связанного состояния в свободное (из валентной зоны в зону проводимости) происходят и обратные переходы, когда электрон проводимости заполняет одну из вакансий и превращается в валентный электрон (возвращается из зоны проводимости в валентную зону). Этот процесс называют рекомбинацией электрона и дырки. В равновесном состоянии устанавливается такая концентрация электронов (и точно такая же концентрация дырок), при которой за единицу времени происходит одинаковое число прямых и обратных переходов.
Дата добавления: 2016-01-29; просмотров: 1469;
