Диаграмма направленности.

В выбранной системе координат (см. рис. 1.20) уравнение параболоида вращения имеет вид:

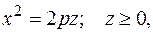(1.20)

где 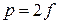– параметр параболы. Линия Oz, проходящая через вершину параболоида и его фокус, называется оптической или фокальной осью. Угол 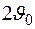, под которым из фокуса F видны края параболоида вращения, называется углом раскрыва зеркала. Круг радиусом 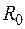образует апертуру (раскрыв) зеркала. Расстояние 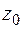от вершины зеркала до раскрыва называют глубиной зеркала. Если 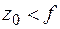( 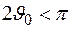), то параболоид вращения является мелким, или длиннофокусным; при 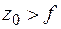( 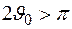) параболоид глубокий, или короткофокусный. Глубина зеркала, радиус раскрыва и фокусное расстояние связаны между собой. 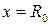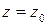Действительно, полагая, что в уравнении (1.20) и , найдем

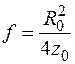. (1.21)

Расчет поля излучения параболоида вращения строгими аналитическими методами осуществить не удается. Из приближенных способов в инженерной практике наибольшее распространение получил апертурный метод. Суть его сводится к приближенной оценке амплитудно-фазового распределения поля на раскрыве зеркала с последующим применением теоремы перемножения; при этом диаграмма направленности элемента излучения представляет ДН источника Гюйгенса, а множитель системы определяется видом амплитудно-фазового распределения на раскрыве и формой излучающей апертуры. Расчет амплитудно-фазового распределения поля на раскрыве осуществляется при следующих допущениях:

токи и касательные составляющие поля на "неосвещенной" поверхности зеркала принимаются равными нулю;

дифракция волн на кромке зеркала не учитывается;

облучатель считается точечным (т.е. его теневой эффект не учитывается);

внутренняя поверхность зеркала располагается в дальней зоне облучателя;

влияние зеркала на характеристики облучателя не учитывается.

Перечисленные допущения существенно упрощают расчет ДН параболоида вращения при удовлетворительном для инженерной практики совпадении результатов расчета с экспериментом в области главного лепестка АДН. Сделанные допущения позволяют для расчета множителя системы непосредственно воспользоваться результатами, полученными при изучении теории излучающего раскрыва. В частности, согласно первым трем допущениям, излучающую апертуру можно считать круглой с радиусом 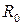. При этом ввиду симметрии антенны амплитуда поля на ее раскрыве является функцией лишь радиальной координаты 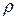, отсчитываемой от центра О' апертуры (см. рис. 1.20). Фазовое распределение можно считать постоянным (при сделанных допущениях волна, отраженная от зеркала, является плоской). Таким образом, справедливо соотношение для ДН круглого синфазного раскрыва:

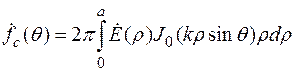. (1.22)

Используя принятые обозначения (см. рис. 1.20) перепишем его в следующем виде:

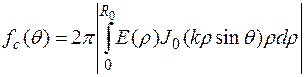. (1.23)

Амплитудное распределение 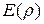зависит от направленных свойств облучателя и геометрических параметров зеркала. Амплитуда сферической волны, создаваемой облучателем, помещенным в фокус зеркала, с расстоянием убывает. Следовательно, в точке А зеркала амплитуда волны обратно пропорциональна расстоянию 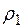от фокуса F до точки А. После отражения от зеркала волна становится плоской и в точке А' апертуры ее амплитуда такая же, как и в точке А. Таким образом, с точностью до постоянного множителя С, не влияющего на форму АДН, можно записать:

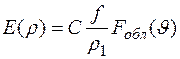, (1.24)

где 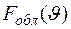– нормированная АДН облучателя.

Величины 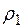и 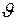связаны с радиальной координатой 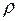раскрыва следующим образом (см. рис. 1.20). Поскольку

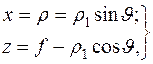
то, учитывая эти равенства в уравнении 1.20, находим:

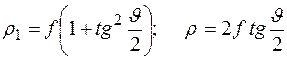. (1.25)

Подставив соотношения (1.23) и (1.24) в выражение (1.22), получим:

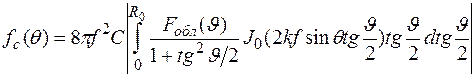. (1.26)

Для упрощения данной формулы отбросим постоянный множитель и введем новую переменную интегрирования – 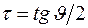. Тогда

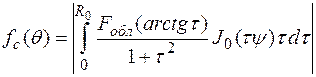, (1.27)

где .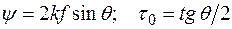

Вычисление множителя системы при заданной АДН облучателя может быть осуществлено с помощью численного интегрирования или с помощью аппроксимации АДН облучателя аналитическим выражением, при котором интеграл (1.27) сводится к табличному. Как правило, используют следующие аппроксимации:

(1.28)

В качестве примера на рис. 1.21 приведены результирующие АДН па-

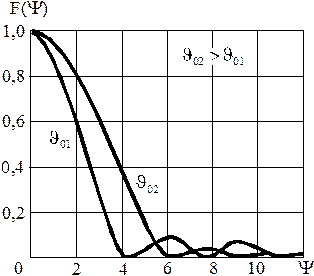Рис. 1.21

раболоида вращения, рассчитанные для двух значений угла раскрыва зеркала. Из графиков видно, что с увеличением угла раскрыва ширина главного лепестка увеличивается, а уровень боковых лепестков уменьшается. Это объясняется увеличением спада амплитудного распределения к краям зеркала. Очевидно, что увеличение ширины АДН облучателя при

заданном угле раскрыва вызывает обратный эффект.