Импульс силы. Импульс тела

Основные динамические величины: сила, масса, импульс тела, момент силы, момент импульса.

Сила – это век­тор­ная ве­ли­чи­на, яв­ля­ю­ща­я­ся мерой дей­ствия на дан­ное тело дру­гих тел или полей.

Сила ха­рак­те­ри­зу­ет­ся:

· Мо­ду­лем

· На­прав­ле­ни­ем

· Точ­кой при­ло­же­ния

В си­сте­ме СИ сила из­ме­ря­ет­ся в нью­то­нах.

_{[F] = H}

Для того чтобы по­нять, что такое сила в один нью­тон, нам нужно вспом­нить, что сила, при­ло­жен­ная к телу, из­ме­ня­ет его ско­рость. Кроме того, вспом­ним о инерт­но­сти тел, ко­то­рая, как мы пом­ним, свя­за­на с их мас­сой. Итак,

Один нью­тон – это такая сила, ко­то­рая ме­ня­ет ско­рость тела мас­сой в 1 кг на 1 м/с за каж­дую се­кун­ду.

При­ме­ра­ми сил могут слу­жить:

· Сила тя­же­сти – сила, дей­ству­ю­щая на тело в ре­зуль­та­те гра­ви­та­ци­он­но­го вза­и­мо­дей­ствия.

· Сила упру­го­сти – сила, с ко­то­рой тело со­про­тив­ля­ет­ся внеш­ней на­груз­ке. Ее при­чи­ной яв­ля­ет­ся элек­тро­маг­нит­ное вза­и­мо­дей­ствие мо­ле­кул тела.

· Сила Ар­хи­ме­да – сила, свя­зан­ная с тем, что тело вы­тес­ня­ет некий объем жид­ко­сти или газа.

· Сила ре­ак­ции опоры – сила, с ко­то­рой опора дей­ству­ет на тело, на­хо­дя­ще­е­ся на ней.

· Сила тре­ния – сила со­про­тив­ле­ния от­но­си­тель­но­му пе­ре­ме­ще­нию кон­так­ти­ру­ю­щих по­верх­но­стей тел.

· Сила по­верх­ност­но­го на­тя­же­ния – сила, воз­ни­ка­ю­щая на гра­ни­це раз­де­ла двух сред.

· Вес тела – сила, с ко­то­рой тело дей­ству­ет на го­ри­зон­таль­ную опору или вер­ти­каль­ный под­вес.

И дру­гие силы.

Сила из­ме­ря­ет­ся с по­мо­щью спе­ци­аль­но­го при­бо­ра. Этот при­бор на­зы­ва­ет­ся ди­на­мо­мет­ром (рис. 1). Ди­на­мо­метр со­сто­ит из пру­жи­ны 1, рас­тя­же­ние ко­то­рой и по­ка­зы­ва­ет нам силу, стрел­ки 2, сколь­зя­щей по шкале 3, план­ки-огра­ни­чи­те­ля 4, ко­то­рая не дает рас­тя­нуть­ся пру­жине слиш­ком силь­но, и крюч­ка 5, к ко­то­ро­му под­ве­ши­ва­ет­ся груз.

Рис. 1. Ди­на­мо­метр (Ис­точ­ник)

На тело могут дей­ство­вать мно­гие силы. Для того чтобы пра­виль­но опи­сать дви­же­ние тела, удоб­но поль­зо­вать­ся по­ня­ти­ем рав­но­дей­ству­ю­щей сил.

Рав­но­дей­ству­ю­щая сил – это сила, дей­ствие ко­то­рой за­ме­ня­ет дей­ствие всех сил, при­ло­жен­ных к телу (Рис. 2).

Зная пра­ви­ла ра­бо­ты с век­тор­ны­ми ве­ли­чи­на­ми, легко до­га­дать­ся, что рав­но­дей­ству­ю­щая всех сил, при­ло­жен­ных к телу – это век­тор­ная сумма этих сил.

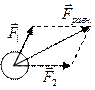
Рис. 2. Рав­но­дей­ству­ю­щая двух сил, дей­ству­ю­щих на тело

Кроме того, по­сколь­ку мы с вами рас­смат­ри­ва­ем дви­же­ние тела в ка­кой-ли­бо си­сте­ме ко­ор­ди­нат, нам обыч­но вы­год­но рас­смат­ри­вать не саму силу, а ее про­ек­цию на ось. Про­ек­ция силы на ось может быть от­ри­ца­тель­ной или по­ло­жи­тель­ной, по­то­му что про­ек­ция – это ве­ли­чи­на ска­ляр­ная. Так, на ри­сун­ке 3 изоб­ра­же­ны про­ек­ции сил, про­ек­ция силы 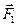– от­ри­ца­тель­на, а про­ек­ция силы 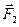– по­ло­жи­тель­на.

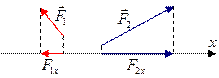
Рис. 3. Про­ек­ции сил на ось

Итак, из этого урока мы с вами углу­би­ли свое по­ни­ма­ние по­ня­тия силы. Мы вспом­ни­ли еди­ни­цы из­ме­ре­ния силы и при­бор, с по­мо­щью ко­то­ро­го из­ме­ря­ет­ся сила. Кроме того, мы рас­смот­ре­ли, какие силы су­ще­ству­ют в при­ро­де. На­ко­нец, мы узна­ли, как можно дей­ство­вать в слу­чае, если на тело дей­ству­ет несколь­ко сил.

Масса, физическая величина, одна из основных характеристик материи, определяющая ее инерционные и гравитационные свойства. Соответственно различают Массу инертную и Массу гравитационную (тяжелую, тяготеющую).

Понятие Масса было введено в механику И. Ньютоном. В классической механике Ньютона Масса входит в определение импульса (количества движения) тела: импульс р пропорционален скорости движения тела v, p = mv (1). Коэффициент пропорциональности - постоянная для данного тела величина m - и есть Масса тела. Эквивалентное определение Массы получается из уравнения движения классической механики f = ma (2). Здесь Масса - коэффициент пропорциональности между действующей на тело силой f и вызываемым ею ускорением тела a. Определенная соотношениями (1) и (2) Масса называется инерциальной массой, или инертной массой; она характеризует динамические свойства тела, является мерой инерции тела: при постоянной силе чем больше Масса тела, тем меньшее ускорение оно приобретает, т. е. тем медленнее меняется состояние его движения (тем больше его инерция).

Действуя на различные тела одной и той же силой и измеряя их ускорения, можно определить отношения Масса этих тел: m₁ : m₂ : m₃... = а₁ : а₂ : а₃...; если одну из Масс принять за единицу измерения, можно найти Массу остальных тел.

В теории гравитации Ньютона Масса выступает в другой форме - как источник поля тяготения. Каждое тело создает поле тяготения, пропорциональное Массе тела (и испытывает воздействие поля тяготения, создаваемого другими телами, сила которого также пропорциональна Массе тел). Это поле вызывает притяжение любого другого тела к данному телу с силой, определяемой законом тяготения Ньютона:

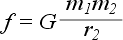(3)

где r - расстояние между телами, G - универсальная гравитационная постоянная, a m₁ и m₂ - Массы притягивающихся тел. Из формулы (3) легко получить формулу для веса Р тела массы m в поле тяготения Земли: Р = mg (4).

Здесь g = G*M/r² - ускорение свободного падения в гравитационном поле Земли, а r » R - радиусу Земли. Масса, определяемая соотношениями (3) и (4), называется гравитационной массой тела.

В принципе ниоткуда не следует, что Масса, создающая поле тяготения, определяет и инерцию того же тела. Однако опыт показал, что инертная Масса и гравитационная Масса пропорциональны друг другу (а при обычном выборе единиц измерения численно равны). Этот фундаментальный закон природы называется принципом эквивалентности. Его открытие связано с именем Г.Галилея, установившего, что все тела на Земле падают с одинаковым ускорением. А.Эйнштейн положил этот принцип (им впервые сформулированный) в основу общей теории относительности. Экспериментально принцип эквивалентности установлен с очень большой точностью. Впервые (1890-1906) прецизионная проверка равенства инертной и гравитационной Масс была произведена Л.Этвешем, который нашел, что Массы совпадают с ошибкой ~ 10^-8. В 1959-64 годах американские физики Р.Дикке, Р.Кротков и П.Ролл уменьшили ошибку до 10^-11, а в 1971 году советские физики В.Б.Брагинский и В.И.Панов - до 10^-12.

Принцип эквивалентности позволяет наиболее естественно определять Массу тела взвешиванием.

Первоначально Масса рассматривалась (например, Ньютоном) как мера количества вещества. Такое определение имеет ясный смысл только для сравнения однородных тел, построенных из одного материала. Оно подчеркивает аддитивность Массы - Масса тела равна сумме Массы его частей. Масса однородного тела пропорциональна его объему, поэтому можно ввести понятие плотности - Массы единицы объема тела.

В классической физике считалось, что Масса тела не изменяется ни в каких процессах. Этому соответствовал закон сохранения Массы (вещества), открытый М.В.Ломоносовым и А.Л.Лавуазье. В частности, этот закон утверждал, что в любой химической реакции сумма Масс исходных компонентов равна сумме Масс конечных компонентов.

Понятие Масса приобрело более глубокий смысл в механике специальной теории относительности А. Эйнштейна, рассматривающей движение тел (или частиц) с очень большими скоростями - сравнимыми со скоростью света с ~ 3 10¹⁰см/сек. В новой механике - она называется релятивистской механикой - связь между импульсом и скоростью частицы дается соотношением:

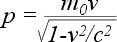(5)

При малых скоростях (v << c) это соотношение переходит в Ньютоново соотношение р = mv. Поэтому величину m₀ называют массой покоя, а Массу движущейся частицы m определяют как зависящий от скорости коэффициент пропорциональности между p и v:

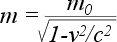(6)

Имея в виду, в частности, эту формулу, говорят, что Масса частицы (тела) растет с увеличением ее скорости. Такое релятивистское возрастание Массы частицы по мере повышения ее скорости необходимо учитывать при конструировании ускорителей заряженных частиц высоких энергий. Масса покоя m₀ (Масса в системе отсчета, связанной с частицей) является важнейшей внутренней характеристикой частицы. Все элементарные частицы обладают строго определенными значениями m₀, присущими данному сорту частиц.

Следует отметить, что в релятивистской механике определение Массы из уравнения движения (2) не эквивалентно определению Массы как коэффициента пропорциональности между импульсом и скоростью частицы, так как ускорение перестает быть параллельным вызвавшей его силе и Масса получается зависящей от направления скорости частицы .

Согласно теории относительности, Масса частицы m связана с ее энергией Е соотношением:

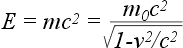(7)

Масса покоя определяет внутреннюю энергию частицы - так называемую энергию покоя Е₀ = m₀с². Таким образом, с Массой всегда связана энергия (и наоборот). Поэтому не существует по отдельности (как в классической физике) закона сохранения Массы и закона сохранения энергии - они слиты в единый закон сохранения полной (т. е. включающей энергию покоя частиц) энергии. Приближенное разделение на закон сохранения энергии и закон сохранения Массы возможно лишь в классической физике, когда скорости частиц малы (v << c) и не происходят процессы превращения частиц.

В релятивистской механике Масса не является аддитивной характеристикой тела. Когда две частицы соединяются, образуя одно составное устойчивое состояние, то при этом выделяется избыток энергии (равный энергии связи) DЕ, который соответствует Массе Dm =DE/с². Поэтому Масса составной частицы меньше суммы Масс образующих его частиц на величину DE/с² (так называемый дефект масс). Этот эффект проявляется особенно сильно в ядерных реакциях. Например, Масса дейтрона (d) меньше суммы Масс протона (p) и нейтрона (n); дефект Масс Dm связан с энергией Е_g гамма-кванта (g), рождающегося при образовании дейтрона: р + n -> d + g, E_g = Dmc². Дефект Массы, возникающий при образовании составной частицы, отражает органическую связь Массы и энергии.

Единицей Массы в СГС системе единиц служит грамм, а вМеждународной системе единиц СИ - килограмм. Масса атомов и молекул обычно измеряется в атомных единицах массы. Масса элементарных частиц принято выражать либо в единицах Массы электрона m_e, либо в энергетических единицах, указывая энергию покоя соответствующей частицы. Так, Масса электрона составляет 0,511 Мэв, Масса протона - 1836,1 m_e, или 938,2 Мэв и т. д.

Природа Массы - одна из важнейших нерешенных задач современной физики. Принято считать, что Масса элементарной частицы определяется полями, которые с ней связаны (электромагнитным, ядерным и другими). Однако количественная теория Массы еще не создана. Не существует также теории, объясняющей, почему Масса элементарных частиц образуют дискретный спектр значений, и тем более позволяющей определить этот спектр.

В астрофизике Масса тела, создающего гравитационное поле, определяет так называемый гравитационный радиус тела R_гр = 2GM/c². Вследствие гравитационного притяжения никакое излучение, в том числе световое, не может выйти наружу, за поверхность тела с радиусом R =< R_гр. Звезды таких размеров будут невидимы; поэтому их назвали "черными дырами". Такие небесные тела должны играть важную роль во Вселенной.

Импульс силы. Импульс тела

По­ня­тие им­пуль­са было вве­де­но еще в пер­вой по­ло­вине XVII века Рене Де­кар­том, а затем уточ­не­но Иса­а­ком Нью­то­ном. Со­глас­но Нью­то­ну, ко­то­рый на­зы­вал им­пульс ко­ли­че­ством дви­же­ния, – это есть мера та­ко­во­го, про­пор­ци­о­наль­ная ско­ро­сти тела и его массе. Со­вре­мен­ное опре­де­ле­ние: им­пульс тела – это фи­зи­че­ская ве­ли­чи­на, рав­ная про­из­ве­де­нию массы тела на его ско­рость:

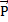= m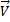

Пре­жде всего, из при­ве­ден­ной фор­му­лы видно, что им­пульс – ве­ли­чи­на век­тор­ная и его на­прав­ле­ние сов­па­да­ет с на­прав­ле­ни­ем ско­ро­сти тела, еди­ни­цей из­ме­ре­ния им­пуль­са слу­жит:

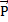[ ] = [ кг· м/с]

Рас­смот­рим, каким же об­ра­зом эта фи­зи­че­ская ве­ли­чи­на свя­за­на с за­ко­на­ми дви­же­ния. За­пи­шем вто­рой закон Нью­то­на, учи­ты­вая, что уско­ре­ние есть из­ме­не­ние ско­ро­сти с те­че­ни­ем вре­ме­ни:

На­ли­цо связь между дей­ству­ю­щей на тело силой, точ­нее, рав­но­дей­ству­ю­щей сил и из­ме­не­ни­ем его им­пуль­са. Ве­ли­чи­на про­из­ве­де­ния силы на про­ме­жу­ток вре­ме­ни носит на­зва­ние им­пуль­са силы. Из при­ве­ден­ной фор­му­лы видно, что из­ме­не­ние им­пуль­са тела равно им­пуль­су силы.

Какие эф­фек­ты можно опи­сать с по­мо­щью дан­но­го урав­не­ния (рис. 1)?

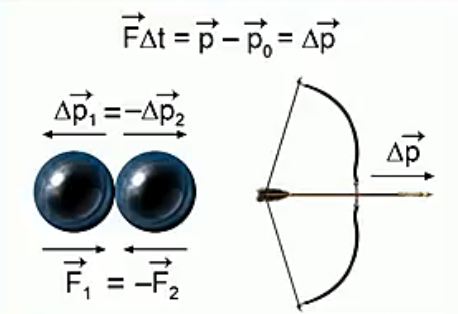
Рис. 1. Связь им­пуль­са силы с им­пуль­сом тела (Ис­точ­ник)

Стре­ла, вы­пус­ка­е­мая из лука. Чем доль­ше про­дол­жа­ет­ся кон­такт те­ти­вы со стре­лой (∆t), тем боль­ше из­ме­не­ние им­пуль­са стре­лы (∆ ), а сле­до­ва­тель­но, тем выше ее ко­неч­ная ско­рость.

Два стал­ки­ва­ю­щих­ся ша­ри­ка. Пока ша­ри­ки на­хо­дят­ся в кон­так­те, они дей­ству­ют друг на друга с рав­ны­ми по мо­ду­лю си­ла­ми, как учит нас тре­тий закон Нью­то­на. Зна­чит, из­ме­не­ния их им­пуль­сов также долж­ны быть равны по мо­ду­лю, даже если массы ша­ри­ков не равны.

Про­ана­ли­зи­ро­вав фор­му­лы, можно сде­лать два важ­ных вы­во­да:

1. Оди­на­ко­вые силы, дей­ству­ю­щие в те­че­ние оди­на­ко­во­го про­ме­жут­ка вре­ме­ни, вы­зы­ва­ют оди­на­ко­вые из­ме­не­ния им­пуль­са у раз­лич­ных тел, неза­ви­си­мо от массы по­след­них.

2. Од­но­го и того же из­ме­не­ния им­пуль­са тела можно до­бить­ся, либо дей­ствуя неболь­шой силой в те­че­ние дли­тель­но­го про­ме­жут­ка вре­ме­ни, либо дей­ствуя крат­ко­вре­мен­но боль­шой силой на то же самое тело.

Со­глас­но вто­ро­му за­ко­ну Нью­то­на, можем за­пи­сать:

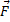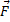∆t = ∆ = ∆ / ∆t

От­но­ше­ние из­ме­не­ния им­пуль­са тела к про­ме­жут­ку вре­ме­ни, в те­че­ние ко­то­ро­го это из­ме­не­ние про­изо­шло, равно сумме сил, дей­ству­ю­щих на тело.

Про­ана­ли­зи­ро­вав это урав­не­ние, мы видим, что вто­рой закон Нью­то­на поз­во­ля­ет рас­ши­рить класс ре­ша­е­мых задач и вклю­чить за­да­чи, в ко­то­рых масса тел из­ме­ня­ет­ся с те­че­ни­ем вре­ме­ни.

Если же по­пы­тать­ся ре­шить за­да­чи с пе­ре­мен­ной мас­сой тел при по­мо­щи обыч­ной фор­му­ли­ров­ки вто­ро­го за­ко­на Нью­то­на:

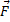= m ,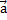

то по­пыт­ка та­ко­го ре­ше­ния при­ве­ла бы к ошиб­ке.

При­ме­ром тому могут слу­жить уже упо­ми­на­е­мые ре­ак­тив­ный са­мо­лет или кос­ми­че­ская ра­ке­та, ко­то­рые при дви­же­нии сжи­га­ют топ­ли­во, и про­дук­ты этого сжи­га­е­мо­го вы­бра­сы­ва­ют в окру­жа­ю­щее про­стран­ство. Есте­ствен­но, масса са­мо­ле­та или ра­ке­ты умень­ша­ет­ся по мере рас­хо­да топ­ли­ва.

МОМЕНТ СИЛЫ - величина, характеризующая вращательный эффект силы; имеет размерность произведения длины на силу. Различают момент силы относительно центра (точки) и относительно оси.

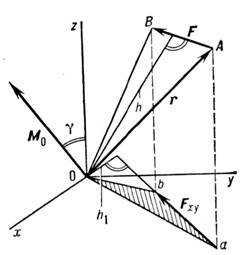
M. с. относительно центра О наз. векторная величина M₀, равная векторному произведению радиуса-вектора r, проведённого из O в точку приложения силы F, на силуM₀ = [rF] или в др. обозначениях M₀ = r 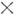F (рис.). Численно M. с. равен произведению модуля силы на плечо h, т. е. на длину перпендикуляра, опущенного из О на линию действия силы, или удвоенной площади

треугольника, построенного на центре O и силе:

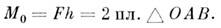
Направлен вектор M₀ перпендикулярно плоскости, проходящей через O и F. Сторона, куда направляется M₀, выбирается условно (M₀ - аксиальный вектор). При правой системе координат вектор M₀ направляют в ту сторону, откуда поворот, совершаемый силой, виден против хода часовой стрелки.

M. с. относительно оси z наз. скалярная величина M_z, равная проекции на ось z вектора M. с. относительно любого центра О, взятого на этой оси; величину M_z можно ещё определять как проекцию на плоскость ху, перпендикулярную оси z, площади треугольника OAB или как момент проекции F_xy силы F на плоскость ху, взятый относительно точки пересечения оси z с этой плоскостью. T. о.,

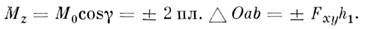
В двух последних выражениях M. с. считается положительным, когда поворот силы F_xy виден с положит. конца оси z против хода часовой стрелки (в правой системе координат). M. с. относительно координатных осей Oxyz могут также вычисляться по аналитич. ф-лам:

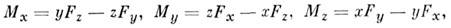
где F_x, F_y, F_z - проекции силы F на координатные оси, х, у, z - координаты точки А приложения силы. Величины M_x, M_y, M_z равны проекциям вектора M₀ на координатные оси.

Если система сил имеет равнодействующую, то момент этой равнодействующей относительно любого центра (или оси) равен сумме моментов всех сил системы относительно того же центра (оси) (см. Вариньона теорема). Понятие о M. с. является одним из осн. понятий механики.

Момент импульса материальной точки относительно точки O определяется векторным произведением
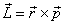, где 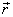— радиус-вектор, проведенный из точки O, 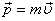— импульс материальной точки.
Момент импульса материальной точки относительно неподвижной оси 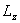равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса 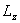не зависит от положения точки O на оси z.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что 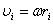, получим
.

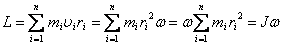Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):
.

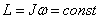Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:
.

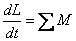Векторное произведение радиуса-вектора 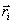материальной точки на ее импульс: 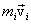называют моментом импульса 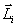, этой точки относительно точки О (рис.5.4)

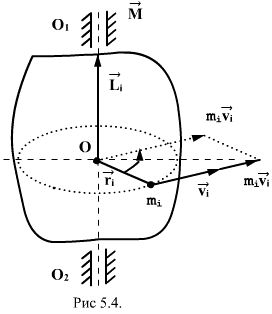
. Вектор 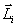иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы 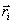и 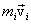и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от 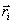к 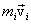происходит против часовой стрелки).

Векторную сумму моментов импульсов 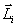всех материальных точек системы называют моментом импульса (количества движения) 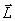системы относительно точки О:

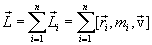
Векторы 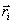и 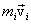взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому 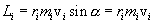. Сучетом связи линейных и угловых величин

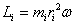
и направлен вдоль оси вращения тела в ту же сторону, что и вектор .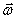

Таким образом.

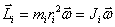
Момент импульса тела относительно оси вращения

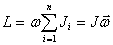
т.е.

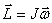
(5.9)

Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси.