Закон Джоуля-Ленца в интегральной и дифференциальной формах

Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов 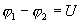, тогда работу по переносу заряда q на этом участке равна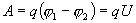

По определению I= q/t. откуда q= I t. Следовательно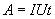

Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил

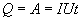
(17.13)

Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности 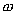, равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника

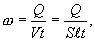
где S - поперечное сечение проводника, 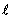- его длина. Используя (1.13) и соотношение 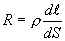, получим

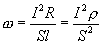
Но 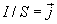- плотность тока, а 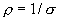, тогда

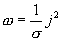
с учетом закона Ома в дифференциальной форме 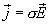, окончательно получаем

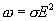
(17.14)

Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.