Тема №4. Трехфазные цепи
4.1. Принципы формирования многофазных электрических цепей
Трехфазной цепью называют совокупность трехфазной системы ЭДС, трехфазной нагрузки и соединительных проводов.
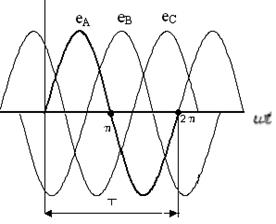
Под трехфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе на 120°. График мгновенных значений и векторная диаграмма ЭДС для симметричной нагрузки изображены на рис. 4.1.а), б).
Трехфазная система получила наибольшее практическое применение благодаря следующим преимуществам:
· передача энергии на дальние расстояния 3-х фазным током наиболее экономична;
· элементы системы наиболее просты в производстве, экономичны и надежны в работе;
· мгновенная мощность при одинаковой нагрузке в фазах генератора неизменна.
 а) б)
а) б)
|
|
|
|
|
|




 в) приемников, однофазных или трехфазных;
в) приемников, однофазных или трехфазных;
|

 |
|
Рис. 4.2.
|
|
|
При подключении нагрузки к обмотке статора генератор отдает нагрузке электрическую энергию.
4.2. Способы соединения трехфазных цепей
Существуют различные схемы соединения обмоток генератора с нагрузкой. Возможно соединение каждой обмотки генератора с нагрузкой двумя проводами, на что потребовалось бы шесть проводов. В целях экономии обмотки трехфазного генератора и нагрузки соединяют по схеме «звезда – звезда» («треугольник»). При этом число соединительных проводов от генератора к нагрузке уменьшается с шести до трех или четырех.
При соединении «звезда» концы трех обмоток объединяют в одну точку (рис. 4.3.), которую называют нулевой (0). Начала обмоток генератора, обозначенные буквами А, В, С, соединяют с нагрузкой.
При соединении обмоток генератора треугольником (рис. 4.4.б) конец первой обмотки соединяют с началом второй, конец второй – с началом третьей, конец третьей – с началом первой. Геометрическая сумма ЭДС в замкнутом треугольнике равна нулю. Поэтому, если к зажимам АВС не присоединена нагрузка, то по обмоткам генератора ток не течет.
|

Рис. 4.3.
Симметричная трехфазовая система ЭДС может быть изображена: 1) графически (рис. 4.1.); 2) векторными диаграммами (рис. 4.2.); 3) тригонометрическими функциями 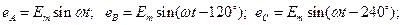

а)
Рис. 4.4.
комплексными числами 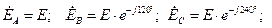
Для трехфазной симметричной системы (рис. 4.1., 4.2.) справедливы уравнения
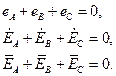
Основными способами соединения являются «звезда – звезда» с нулевым проводом (рис. 4.5.), либо без нулевого (нейтрального) провода N, и «треугольник – треугольник» (рис. 4.6.). Возможны также соединения: «треугольник – звезда» и «звезда – треугольник».
Провод, соединяющий нулевые точки О генератора и О/ нагрузки при соединении звездой, называют нейтральным или нулевым проводом, а ток в нулевом проводе − нулевым током. За положительное направление нулевого тока принято от О/ к О.
Провода, соединяющие точки А, В, С генератора и нагрузки, называют линейными проводами, а текущие по ним токи – линейными IA, IB, IC. За положительное направление для них принято от генератора к нагрузке. Модули линейных токов обозначают Iл.
Напряжение между линейными проводами называют линейным и обозначают двумя индексами, например, UAB (между точками А и В). Модуль линейного напряжения обозначают Uл.
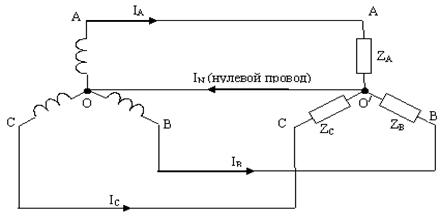
Рис. 4.5.

Рис. 4.6.
Каждую из трех обмоток генератора называют фазой генератора, каждую из трех нагрузок − фазой нагрузки, а протекающими по ним токи − фазовыми токами генератора и нагрузки Iф; а напряжения Uф на них называют фазовыми.
Соотношения между линейными и фазовыми напряжениями следующие. При соединении генератора в «звезду» линейное напряжение UЛ = UАВ по модулю в 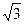 больше фазового напряжения генератора Uф
больше фазового напряжения генератора Uф 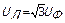 .
.
|
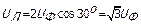 .
.
Линейный ток Iл при соединении генератора звездой равен фазовому току генератора 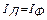 .
.

Рис. 4.7.
При соединении генератора в «треугольник», как видно из рис. 4.6. линейное напряжение равно фазовому напряжению генератора 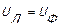 ,
,
а линейный ток Iл в 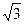 раза больше фазового тока
раза больше фазового тока 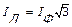 .
.
При соединении нагрузки треугольником положительные направления для токов выбирают по часовой стрелке. Первый индекс отвечает точке, от которой ток утекает, второй – точке, к которой притекает. Линейные токи не равны фазным токам нагрузки и определяются через них по первому закону Кирхгофа 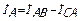 ,
, 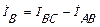 ,
, 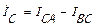 .
.
Из векторной диаграммы (рис. 4.7.) по теореме косинусов 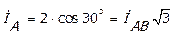 ,
,
аналогично
|
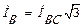 ,
, 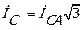 ,или общем случае
,или общем случае 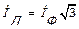 .
.
3.3. Расчет трехфазных цепей при соединении звездой
Для расчета токов должна быть задана схема цепи, значение и тип сопротивлений, напряжение источника энергии. Расчеты обычно проводят для комплексных значений.
Симметричная нагрузка в схеме соединением «звезда – звезда» с нулевым проводом представлена на рис. 4.8.
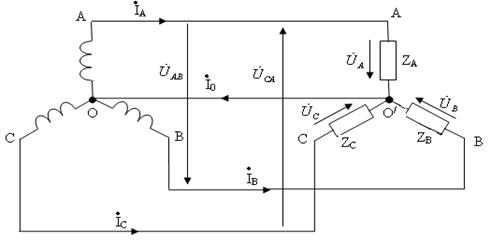
Рис. 4.8.
Если нулевой провод в схеме симметричного приемника ( 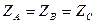 ) обладает весьма малым сопротивлением (Z0 = 0), то потенциал точки О/ практически равен потенциалу точки О, и точки сливаются в одну. В схеме образуются три обособленных контура, комплексные значения токов в каждом из которых определяются как в однофазной цепи
) обладает весьма малым сопротивлением (Z0 = 0), то потенциал точки О/ практически равен потенциалу точки О, и точки сливаются в одну. В схеме образуются три обособленных контура, комплексные значения токов в каждом из которых определяются как в однофазной цепи 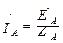 ;
; 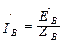 ;
; 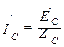
где ĖА, ĖВ, ĖС – фазные напряжения на зажимах генератора.
По первому закону Кирхгофа ток в нулевом проводе 4-х проводной системы равен геометрической сумме фазных токов 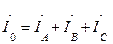 .
.
В общем случае комплексное напряжение между нулевыми точками 0 – 0` при наличии нейтрального провода 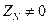
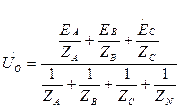 .
.
При равномерной симметричной нагрузке ток I0=0, и нулевой провод может быть изъят из схемы без изменения ее режима работы. Для 3-х проводной системы, т.е. не содержащей нейтральный провод (ZN = ∞) слагаемое 1/ ZN в знаменателе будет отсутствовать.
При определении напряжения фаз приемника если не учитывать сопротивления источника, то 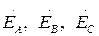 можно заменить на
можно заменить на 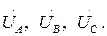
Переходя к действующим значениям величин в случае, когда нагрузки во всех фазах равны и имеют активный характер 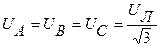 ,
,
где 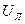 − значение линейного напряжения, токи соответственно принимают значения
− значение линейного напряжения, токи соответственно принимают значения 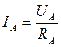 ,
, 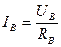 ,
, 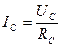 .
.
Общая мощность трехфазной цепи с активной нагрузкой равна
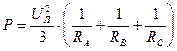 .
.
4.4. Несимметричная нагрузка при соединении звездой
При несимметричной нагрузке и отсутствии нулевого провода между нулевыми точками генератора О и приемника О/ появляется напряжение 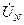 , в результате чего фазные напряжения приемника оказываются различными. Расчетные соотношение
, в результате чего фазные напряжения приемника оказываются различными. Расчетные соотношение 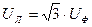 между фазными и линейными напряжениями при этом нарушается. Для определения напряжения между нулевыми точками, а также фазных напряжений приемника предположим, что в электрической цепи имеется нейтральный (нулевой) провод, сопротивление которого
между фазными и линейными напряжениями при этом нарушается. Для определения напряжения между нулевыми точками, а также фазных напряжений приемника предположим, что в электрической цепи имеется нейтральный (нулевой) провод, сопротивление которого 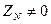 . Тогда напряжение между нулевыми точками источника и приемника
. Тогда напряжение между нулевыми точками источника и приемника
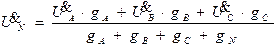 ,
,
где g A, g B, g C, g N – проводимости фазных и нулевого проводов,
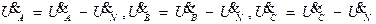
|
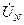 в знаменателе учитывается проводимость нейтрального провода gN..
в знаменателе учитывается проводимость нейтрального провода gN..
На рис. 4.9. приведена векторная диаграмма без нейтрального провода, на которой 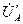 ,
, 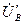 ,
, 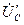 − векторы фазных напряжений источника, а
− векторы фазных напряжений источника, а 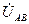 ,
, 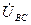 ,
, 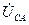 − векторы линейных напряжений источника, а также линейных напряжений приемника. Для построения вектора напряжения
− векторы линейных напряжений источника, а также линейных напряжений приемника. Для построения вектора напряжения 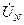 и векторов фазных напряжений приемника
и векторов фазных напряжений приемника 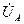 ,
, 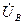 ,
, 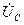 используем их значения, полученные выше.
используем их значения, полученные выше.

Рис. 4.9.
Связь между фазными и линейными векторами 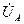 ,
, 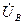 ,
, 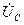 и
и 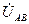 ,
, 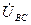 ,
, 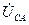 ,определяем выражениями
,определяем выражениями 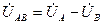 ,
, 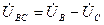 ,
, 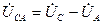 .
.
Векторная диаграмма построена для активной несимметричной нагрузки фаз ( 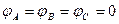 ).
).
При изменении величины фазных активных сопротивлений напряжение 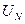 может изменяться в широких пределах. В соответствии с этим точка N на диаграмме может занимать различные положения, а фазовые напряжения приемника могут отличаться друг от друга весьма существенно.
может изменяться в широких пределах. В соответствии с этим точка N на диаграмме может занимать различные положения, а фазовые напряжения приемника могут отличаться друг от друга весьма существенно.
Рассмотрим, частный случай несимметричной нагрузки, когда 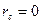 . Поскольку
. Поскольку 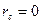 , то и
, то и 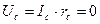 , получим
, получим 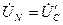 ,
, 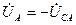 и
и 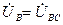 . Точка N на диаграмме переместится в точку С, напряжение
. Точка N на диаграмме переместится в точку С, напряжение 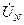 возрастет до фазного напряжения источника, а напряжения
возрастет до фазного напряжения источника, а напряжения 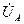 ,
, 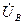 −до линейных напряжений.
−до линейных напряжений.

Рис. 4.10.
При изменении фазных напряжений происходит изменение фазных токов и мощностей − «перекос фаз».
Если при несимметричной нагрузке нулевые точки источника и приемника соединить нулевым проводом, то поскольку сопротивление нулевого провода мало, ( 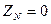 и
и 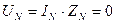 ), то фазные напряжения приемника получаются одинаковыми и сдвинутыми по фазе относительно друг друга на угол
), то фазные напряжения приемника получаются одинаковыми и сдвинутыми по фазе относительно друг друга на угол 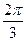 . Включение нулевого провода приводит к соответствующим изменениям векторной диаграммы электрической цепи. Так, если электрической цепи без нулевого провода соответствует векторная диаграмма, изображенная на рис.3.9. сплошной линией, то той же цепи при включении нулевого провода соответствует диаграмма, изображенная на том же рисунке пунктиром.
. Включение нулевого провода приводит к соответствующим изменениям векторной диаграммы электрической цепи. Так, если электрической цепи без нулевого провода соответствует векторная диаграмма, изображенная на рис.3.9. сплошной линией, то той же цепи при включении нулевого провода соответствует диаграмма, изображенная на том же рисунке пунктиром.
Вектор 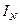 построен в соответствии с выражением.
построен в соответствии с выражением. 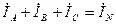 .
.
При наличии нулевого провода в схемах с несимметричной нагрузкой, так же как и в случае с симметричной нагрузкой остается в силе соотношение
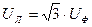 .
.
На основании изложенного можно сделать вывод, что нулевой провод необходим для того, чтобы при несимметричной нагрузке выравнивать фазные напряжения приемника, т.е. получать во всех фазах приемника одинаковые напряжения, равные 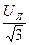 .
.
Фазные токи, углы сдвига фаз между фазовыми напряжениями и токами, а также фазные мощности при несимметричной нагрузке в цепи с нулевым проводом будут в общем случае различными. Они могут быть определены по следующим формулам: 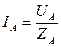 ,
, 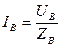 ,
, 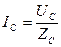 .
.
Углы сдвига фаз между фазными токами и напряжениями зависят от величины и характера сопротивлений фаз приемника и равны
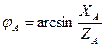 ,
, 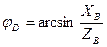 ,
, 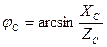 .
.
Мощности для фазы «А» равны
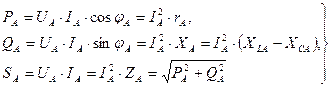
Активная и реактивная мощности трехфазного приемника при соединении звездой 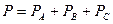 ,
, 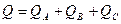 .
.
Если кроме фазных токов требуется найти ток в нулевом проводе, то задачу следует решать в комплексной форме. При этом необходимо прежде всего выразить в комплексной форме то 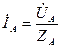 ,
, 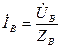 ,
, 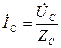
Ток в нулевом проводе можно определить также по векторной диаграмме, не прибегая к решению задачи в комплексной форме.
4.5. Расчет трехфазных цепей соединением треугольник
|
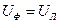 .
.
Таким образом, соединение треугольником следует применять тогда, когда каждая фаза трехфазного приемника рассчитана на напряжение, равное номинальному линейному напряжению сети.

Рис. 4.11.
Фазные токи 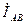 ,
, 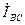 ,
, 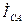 в общем случае не равны линейным токам
в общем случае не равны линейным токам 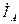 ,
, 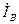 ,
, 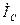 и могут быть найдены по следующим соотношениям:
и могут быть найдены по следующим соотношениям:
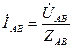 ,
, 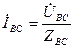 ,
, 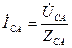 .
.
Линейные токи 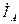 ,
, 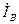 ,
, 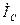 могут быть определены через значения фазных токов. Из первого закона Кирхгофа запишем:
могут быть определены через значения фазных токов. Из первого закона Кирхгофа запишем:
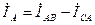 ,
, 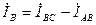 ,
, 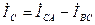 .
.
Использую указанные соотношения и имея векторы фазных токов, можно построить векторную диаграмму линейных токов (рис. 4.12.).

При симметричной нагрузке соединением «треугольник» равны в отдельности активные и полные реактивные сопротивления всех фаз 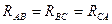 ,
, 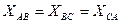
Однако, как правило, однофазные приемники подключаются не одновременно. Нагрузку можно считать симметричной лишь тогда, когда включены все приемники. Для каждой фазы могут быть использованы все методы расчета, рассмотренные ранее применительно к однофазной цепи с одним источником. Зная, например, фазные напряжения и сопротивления, можно по закону Ома найти фазные токи по формулам 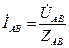 ,
, 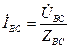 ,
, 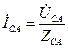
При симметричной нагрузке, 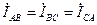 ,
, 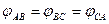 -фазные токи равны друг другу и сдвинуты по фазе относительно соответствующих фазных напряжений на одинаковые углы.
-фазные токи равны друг другу и сдвинуты по фазе относительно соответствующих фазных напряжений на одинаковые углы.
|
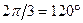 .
.
Векторы линейных токов 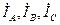 изображают результирующими векторов фазных токов, как показано на рис. 4.13. Из векторной диаграммы следует, что
изображают результирующими векторов фазных токов, как показано на рис. 4.13. Из векторной диаграммы следует, что 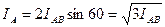 .
.

Рис. 4.13.
Такое же соотношение существует между любыми другими фазными и линейными токами. Поэтому можно написать, что при симметричной нагрузке
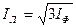 .
.
Зная фазные напряжения, токи и углы сдвига фаз между ними, либо токи и сопротивления, можно найти фазные мощности. Например, мощности фазы АВ будут равны
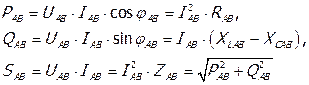
Таким же путем находим мощности фаз ВС и СА. В силу равенства напряжений, токов, углов сдвига фаз и сопротивлений при симметричной нагрузке 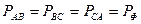 ,
, 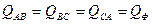 ,
, 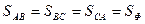 .
.
При симметричной нагрузке активная Р, реактивная Q и полная S мощности трехфазного приемника 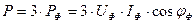 ,
, 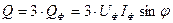 ,
,
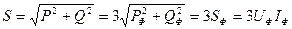 .
.
В качестве номинальных напряжений и токов трехфазных приемников указываются обычно линейные напряжения и токи. Учитывая это, мощности трехфазных приемников желательно также выражать через линейные напряжения и токи 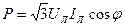 ,
, 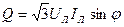 ,
, 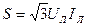 .
.
4.6. Несимметричные нагрузки при соединении треугольником
Несимметричной нагрузкой считают такую, при которой активное или реактивное сопротивление хотя бы одной из фаз не равно сопротивлениям других фаз (рис. 4.14.) rAB = rBC = rC; XAB=XBC≠X CA. В таком случае при несимметричной нагрузке ZAB ≠ ZBC ≠ ZCA.
Фазные токи, углы сдвига фаз между фазными напряжениями и токами, а также мощности могут быть определены по формулам
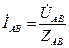 ,
, 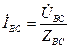 ,
, 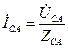
Так как 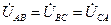 , а при несимметричной нагрузке ZAB ≠ ZBC ≠ ZCA, то
, а при несимметричной нагрузке ZAB ≠ ZBC ≠ ZCA, то 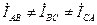 .
.
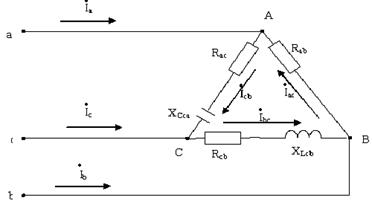
Рис. 4.14.
Углы сдвига фаз между фазными токами и напряжениями зависят от величины и характера сопротивлений фаз и могут быть определены следующим образом 
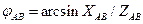 ;
; 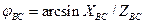 ;
; 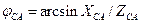 .
.
Т.о., при несимметричной нагрузке фазные токи, углы сдвига фаз и фазные мощности в общем случае различные.
Зная фазные напряжения, токи и углы сдвига фаз между ними, либо токи и сопротивления, можно найти фазные мощности. Например, мощности фазы AB

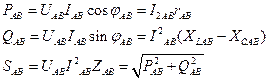
Активные и реактивные мощности приемника 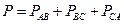 ;
; 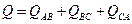 .
.
Векторная диаграмма при несимметричной нагрузке для случая, когда в фазе AB имеется активное сопротивление, в фазе BC – активное и индуктивное сопротивления, фазе CA – активное и емкостное сопротивления, приведена на рис. 4.15. Построение векторов линейных токов произведено в соответствии с выражениями 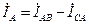 ,
, 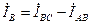 ,
, 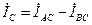 .
.
 Если кроме фазных токов, требуется определить линейные токи, то их можно так же определить по векторной диаграмме, не прибегая к решению задачи в комплексной форме.
Если кроме фазных токов, требуется определить линейные токи, то их можно так же определить по векторной диаграмме, не прибегая к решению задачи в комплексной форме.
Рис. 4.15.
|
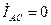 ; фазные токи
; фазные токи 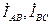 , а также углы φAB, φ BC не изменятся, а линейные токи
, а также углы φAB, φ BC не изменятся, а линейные токи 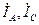 уменьшатся и будут равны
уменьшатся и будут равны 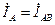 ,
, 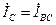 .
.
Дата добавления: 2016-01-26; просмотров: 1603;
