Метод сопряженных градиентов.
Этот метод применяется к СЛАУ
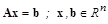
с симметрической положительно-определенной 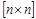 -матрицей A:
-матрицей A: 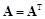 ,
, 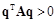
для любого q.
Его можно считать итерационным, так как решение ищется в виде
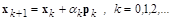 ,
,
где 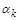 – параметр,
– параметр, 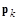 – так называемый вектор сопряженного гради-ента, k – номер итерации.
– так называемый вектор сопряженного гради-ента, k – номер итерации.
С другой стороны, пусть построена последовательность
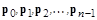 .
.
И пусть эта последовательность векторов является линейно-независимой и образует базис пространства 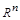 . В этом случае любой вектор пространства
. В этом случае любой вектор пространства 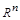 , и в частности вектор
, и в частности вектор 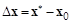 , может быть представлен в виде разложения по базису
, может быть представлен в виде разложения по базису
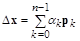
и, следовательно,
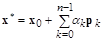 ,
,
или
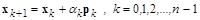 .
.
Таким образом, число итераций, необходимое для вычисления точного решения в отсутствии ошибок округления, известно и равно n. По этой причине метод можно считать прямым, так как заранее можно подсчитать число арифметических операций, требуемых для получения решения.
Построим метод сопряженных градиентов. Предположим, что на k-й итерации каким-либо способом вычислено 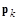 . Тогда
. Тогда
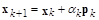 .
.
Как вычислить параметр 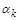 ? Рассмотрим квадратичную функцию
? Рассмотрим квадратичную функцию
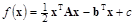 .
.
Минимум этой квадратичной функции достигается на решении системы 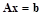 . Итерационный процесс метода сопряженных градиентов можно рассматривать как процесс поиска минимума функции
. Итерационный процесс метода сопряженных градиентов можно рассматривать как процесс поиска минимума функции  . Параметр
. Параметр 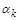 на k-й итерации следует выбирать таким образом, чтобы функция
на k-й итерации следует выбирать таким образом, чтобы функция  в направлении
в направлении 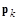 достигала минимального значения, т. е.
достигала минимального значения, т. е.
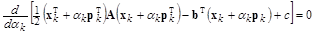 .
.
Отсюда
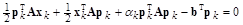 .
.
Так как
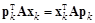 ,
, 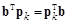 ,
,
то
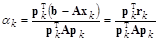 ,
,
где 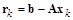 – текущий вектор невязки.
– текущий вектор невязки.
Невязку 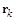 в методе сопряженных градиентов можно вычислить другим, более экономичным способом. Действительно,
в методе сопряженных градиентов можно вычислить другим, более экономичным способом. Действительно,
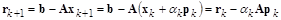 .
.
Вычислив лишь 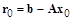 , на последующих шагах невязку можно корректировать из соотношения
, на последующих шагах невязку можно корректировать из соотношения
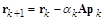 .
.
Так как  вычислено при расчете
вычислено при расчете 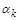 , для нахождения
, для нахождения 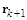 потребуются лишь незначительные вычислительные затраты.
потребуются лишь незначительные вычислительные затраты.
Рассмотрим теперь, как строятся на итерациях векторы сопряженных градиентов. Два вектора 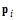 и
и  являются сопряженными, или иначе A-ортогональными, если
являются сопряженными, или иначе A-ортогональными, если
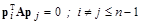 .
.
Примем в качестве начального сопряженного градиента вектор 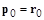 , где
, где 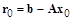 . Построим следующее правило расчета сопряженного градиента:
. Построим следующее правило расчета сопряженного градиента:
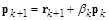 .
.
Выберем параметр 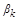 таким образом, чтобы векторы
таким образом, чтобы векторы 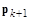 и
и 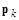 были сопряженными. Умножим это соотношение слева сначала на матрицу A, затем на вектор
были сопряженными. Умножим это соотношение слева сначала на матрицу A, затем на вектор 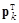 :
:
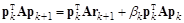 .
.
Если учесть, что 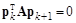 , нетрудно получить расчетное соотношение для параметра
, нетрудно получить расчетное соотношение для параметра 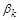 :
:
 .
.
В итоге метод сопряженных градиентов можно представить следующим алгоритмом расчета:
1. Вычислить 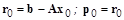 .
.
2. Вычислить в цикле (k=0,1,2,…):
2.1. 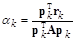 (
(  – запомнить);
– запомнить);
2.2. 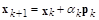 ;
;
2.3. 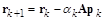 ;
;
2.4. 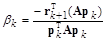 ;
;
2.5. 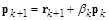 .
.
Теоретически векторы 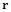 и
и 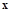 , построенные по этому алгоритму, должны удовлетворять условиям
, построенные по этому алгоритму, должны удовлетворять условиям
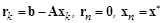 .
.
Однако из-за наличия ошибок округления эти соотношения выполняются приближенно. Полученное после 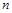 итераций решение
итераций решение 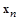 может значительно отличаться от точного решения. Последнее не происходит, если число итераций превышает
может значительно отличаться от точного решения. Последнее не происходит, если число итераций превышает 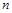 . Рано или поздно наступает такой момент, когда норма вектора невязки начинает резко уменьшаться и в конечном итоге точность решения определяется числом обусловленности матрицы
. Рано или поздно наступает такой момент, когда норма вектора невязки начинает резко уменьшаться и в конечном итоге точность решения определяется числом обусловленности матрицы 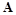 (например, при работе с 15-и разрядными десятичными числами при числе обусловленности 106 можно получить в решении в лучшем случае только девять точных цифр).
(например, при работе с 15-и разрядными десятичными числами при числе обусловленности 106 можно получить в решении в лучшем случае только девять точных цифр).
Приведем в заключение оценку времени выполнения итерации метода сопряженных градиентов при решении СЛАУ с пятидиагональной матрицей A:
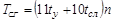 .
.
Дата добавления: 2016-01-26; просмотров: 849;
