Метод неполной факторизации.
Этот метод при построении матрицы расщепления Q использует вид структуры матрицы A.
Пусть требуется решить систему
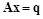 ,
,
матрица которой имеет пятидиагональную структуру (рис. 5.1). Выбе-рем в качестве матрицы расщепления матрицу
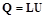 ,
,
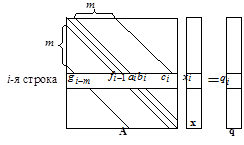
Рис. 5.1. Решаемая СЛАУ
в которой структура нижней треугольной матрицы L совпадает со структурой матрицы 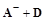 , структура верхней треугольной матрицы U совпадает со структурой матрицы
, структура верхней треугольной матрицы U совпадает со структурой матрицы 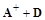 .
.
Для пятидиагональной матрицы A матрица расщепления Q имеет семидиагональный вид (рис. 5.2):
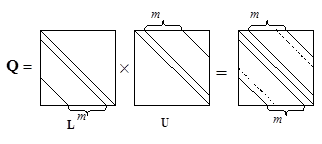
Рис. 5.2. Матрица расщепления пятидиагональной матрицы
Значения элементов матриц L и U выберем таким образом, чтобы элементы пяти диагоналей матрицы A совпадали с аналогичными элементами матрицы Q (рис. 5.3). Перемножим i–ю строку матрицы L последовательно на столбцы матрицы U и результат приравняем к соответствующим элементам i-й строки матрицы Q. Воспользуемся
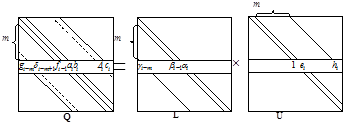
Рис. 5.3. К определению элементов матриц L и U
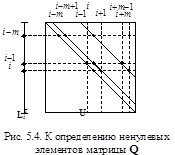 следующим рисунком, иллюстри-рующим процесс вычисления ненулевых элементов в Q (рис. 5.4).
следующим рисунком, иллюстри-рующим процесс вычисления ненулевых элементов в Q (рис. 5.4).
На этом рисунке 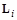 – i-я строка матрицы L, Т – признак транспонирования, верхние индексы обозначают номера столбцов матрицы Q, в которых находятся ненулевые элементы ее i-й строки.
– i-я строка матрицы L, Т – признак транспонирования, верхние индексы обозначают номера столбцов матрицы Q, в которых находятся ненулевые элементы ее i-й строки.
Выпишем искомые соотношения:
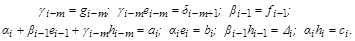
Отсюда
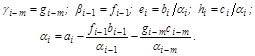
Таким образом, для расчета элементов матриц L и U необходимо вычислить дополнительно лишь один массив a, разместив его на месте массива a.
Обозначим
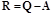
и перепишем итерационный метод
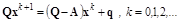
в виде
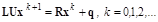 .
.
Это и есть итерационная схема метода неполной факторизации. Матрица R здесь имеет двухдиагональную структуру (рис. 5.5), а расчетные соотношения для ее элементов такие:
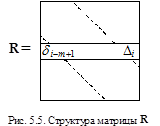
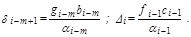
Подчеркнем, что массивы α, β, Δ вычисляются однократно (до цикла).
В итоге расчетная схема итерационного метода неполной факторизации выглядит следующим образом:
1. Вычислить массивы α,β, Δ.
2. Вычислить в цикле (k=0,1,2,…):
2.1. 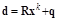 ;
;
2.2. 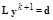 ;
; 
2.3. 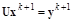 .
.
Оценим время выполнения одной итерации. Для этого распишем пункт 2 алгоритма в координатной форме:
2.1. 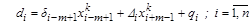 .
.
2.2. 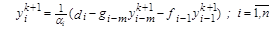 .
.
2.3. 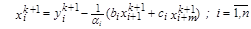 .
.
Непосредственный подсчет показывает, что время выполнения одной итерации метода неполной факторизации при решении линейной системы с пятидиагональной матрицей составляет
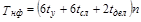 .
.
Полные затраты рассмотренных итерационных методов на решение линейных систем с пятидиагональной матрицей приведены в табл. 5.1.
Таблица 5.1
| Метод | Затраты |
| Якоби | 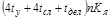
|
| Г.-З. | 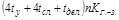
|
| ПР | 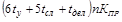
|
| НФ | 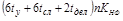
|
Затраты на итерациях этих методов, вообще говоря, сравнимы. Эффективность метода неполной факторизации достигается за счет сокращения полного числа итераций (как правило, 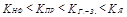 ).
).
Дата добавления: 2016-01-26; просмотров: 1103;
