ЖЕЛЕЗОБЕТОННЫХ И КАМЕННЫХ КОНСТРУКЦИЙ 3 страница
А. При площади сечения промежуточных стержней, расположенных у граней, параллельных рассматриваемой плоскости, менее 1/3 (As+A  )
)
| 0,93 | 0,92 | 0,91 | 0,9 | 0,89 | 0,87 | 0,84 | 0,81 | |
| 0,5 | 0,92 | 0,92 | 0,91 | 0,9 | 0,87 | 0,84 | 0,80 | 0,75 |
| 1,0 | 0,92 | 0,91 | 0,9 | 0,88 | 0,86 | 0,82 | 0,77 | 0,70 |
Б. При площади сечения промежуточных стержней, расположенных у граней, параллельных рассматриваемой плоскости, не менее 1/3 (As+A  )
)
| 0,92 | 0,92 | 0,91 | 0,89 | 0,87 | 0,84 | 0,80 | 0,75 | |
| 0,5 | 0,92 | 0,91 | 0,9 | 0,87 | 0,83 | 0,79 | 0,72 | 0,65 |
| 1,0 | 0,92 | 0,91 | 0,89 | 0,86 | 0,8 | 0,74 | 0,66 | 0,58 |
N≤φ [ηb(RbA+RscAs)+ηrcrArcr(Rb,rcr+0.01Rsc,rcr)]. (5.3)
Коэффициент продольного изгиба φ усиленной колонны, учитывающий длительность загружения, гибкость и характер ее армирования, определяется по экспериментальной зависимости
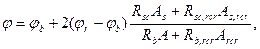 (5.4)
(5.4)
где φb и φr — определяются по табл. 5.1.
В (5.3) φ принимается не более φr. Для определения φ по формуле (5.4) необходимо предварительно задаться минимальной толщиной обоймы 50 мм, при этом наименьший размер поперечного сечения усиленной колонны будет b/=b+2d (рис. 5.25).
Формула (5.4) справедлива при усилении колонны на всю высоту. При усилении колонны только в пределах перегруженных и поврежденных участков φ следует также определять по формуле (5.4), как для колонны до усиления без учета сечения обоймы Arcr и дополнительной арматуры As,rcr
Площадь сечения бетона обоймы усиления определяется по формуле:
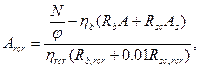 (5.5)
(5.5)
а расчетная толщина монолитной железобетонной обоймы по формуле:
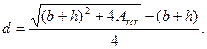 (5 6)
(5 6)
Площадь сечения продольной дополнительной арматуры определяется из условия (5.2), а прочность усиленной колонны проверяется по формуле (5.3) с учетом полученных при расчете значений φ и As,rcr. Формула (5.3) приемлема, когда нагрузка передается на обойму, имеющую опору снизу. Если нагрузка передается на обойму, не имеющую опоры снизу, то к Rb,rcr в формулах (5.1), (5.3) вводится коэффициент условий работы равный 0,7; при отсутствии непосредственной передачи нагрузки на обойму этот коэффициент равен 0,35.
Расчет прочности железобетонных колонн работающих со случайным эксцентриситетом и усиленных поверхностно-оклеечным стеклопластиком производится исходя из условия.
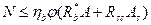 , (5.7)
, (5.7)
где R 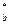 - приведенная призменная прочность бетона усиленной конструкции; значения N, ηb, φ, Rsc, A и As приведены выше.
- приведенная призменная прочность бетона усиленной конструкции; значения N, ηb, φ, Rsc, A и As приведены выше.
Приведенная призменная прочность бетона определяется по формуле
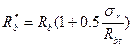 , (5.8)
, (5.8)
где Rb и Rbt — призменная прочность и прочность бетона на осевое растяжение усиливаемой конструкции, соответствующее фактической кубиковой прочности по результатам испытаний неразрушающими методами; σr — дополнительное напряжение в бетоне, вызванное работой поверхностно-оклеечного стеклопластика, которое рекомендуется определять для предельного состояния по формуле
σr = (2nfPf)/b, (5.9)
где nf — количество слоев стеклоткани в стеклопластике; b — ширина усиливаемой колонны; Rf — расчетная прочность на растяжение 1 см стеклопластика из одного слоя стеклоткани, принимаемое по табл. 14 [33].
Расчетное значение (nf) и характеристика (Rf) поверхностно-оклеечного стеклопластика подбирается по табл. 14[33], при этом необходимо соблюдать условие
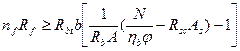 . (5.10)
. (5.10)
С методикой расчета внецентренно сжатых элементов при загружении продольной силой с расчетным эксцентриситетом при усилении их односторонним наращиванием, обоймой и двусторонним наращиванием, а также металлическими обоймами и предварительно напряженными распорками можно ознакомиться в работах [23, 55].
2. Изгибаемые железобетонные элементы
Расчет изгибаемых элементов, усиленных обоймами, рубашками, наращиванием или установкой в тело конструкции дополнительной арматуры на полимеррастворе производят также, как балок с увеличенным сечением бетона и арматуры (рис. 5.26, а). Обычно толщина обоймы или наращивания в растянутой зоне элемента задается. Количество дополнительной арматуры определяют по формуле
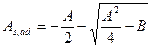 , при Rs,ad = Rs, (5.11)
, при Rs,ad = Rs, (5.11)
Где параметры А и В определяют по формулам
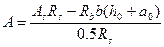 (5.12)
(5.12)
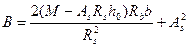 (5.13)
(5.13)
Величину сжатой зоны железобетонного сечения определяют по формуле
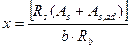 (5.14)
(5.14)
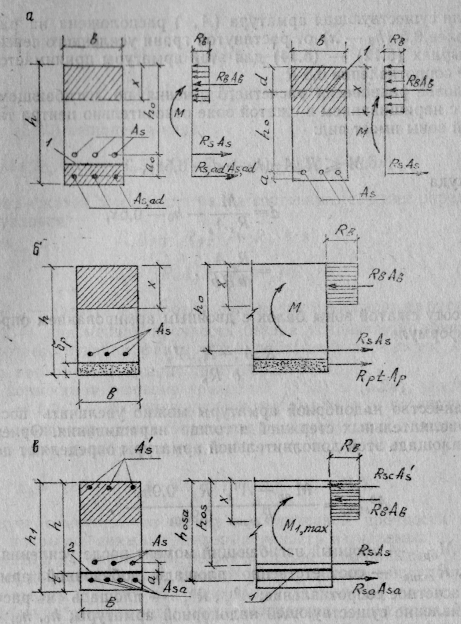
Рис. 5.26. Расчетная схема усиления изгибаемых элементов
а — наращиванием; б — покрытием из полимерраствора;
в — приклеиванием железобетонных элементов;
1 — адгезионная обмазка полимерраствором; 2 — полимеррастворный шов
Если существующая арматура (As) расположена на расстоянии более 0,5 (h0 — х) от растянутой грани усиленного сечения, то в формулах (5.12) — (5.14) для этой арматуры принимается расчетное сопротивление 0,8Rs.
Условие равновесия расчетного сечения по изгибающему моменту с наращиванием в сжатой зоне относительно центра тяжести сжатой зоны имеет вид:
М ≤ RsАs (h0+d—0,5x), (5.15)
откуда
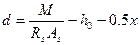 , (5.16)
, (5.16)
где
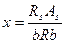 (5.17)
(5.17)
Высоту сжатой зоны балок с двойным армированием определяют по формуле
х = 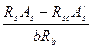 (5.18)
(5.18)
Количество надопорной арматуры можно увеличить постановкой дополнительных стержней в толще наращивания. Ориентировочно площадь этой дополнительной арматуры определяют по формуле
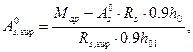 (5.19)
(5.19)
где Мар — опорный изгибающий момент после усиления; As,sup, Rs,sup — соответственно площадь добавочной арматуры и ее расчетное сопротивление; A 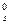 , R
, R 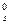 — площадь и расчетное сопротивление существующей надопорной арматуры; h0, h01 — рабочая высота надопорного сечения до наращивания и после наращивания.
— площадь и расчетное сопротивление существующей надопорной арматуры; h0, h01 — рабочая высота надопорного сечения до наращивания и после наращивания.
Условие прочности изгибаемого элемента с полимеррастворным покрытием в растянутой зоне (рис. 5.26, б) по изгибающему моменту относительно центра тяжести сжатой зоны сечения имеет вид
М ≤ Мb + к Мр , (5.20)
где М — изгибающий момент, воспринимаемый сечением составной балки; Мb — изгибающий момент, воспринимаемый железобетонной балкой без покрытия; Мр — изгибающий момент, воспринимаемый полимерным покрытием; к — коэффициент условий работы полимерного покрытия растянутой зоны балки составного сечения, учитывающий усадочные напряжения, появление трещин полимеррастворе до разрушения и т. п., принимаемый равным 0,65.
Учитывая, что
Мb = RsАs(h0-0,5х), (5.21)
Мр = RptAp(h0-0,5δp-0,5x), (5.22)
формулу (5.20) запишем в виде
М≤RsAs(h0—0,5x) + кRрА (h0-0,5δp — 0,5x). (5.23)
Высота сжатой зоны х для балки составного сечения определяется из условия
RsAs+RptАр=Rbbх
или
х = (RsAs+RptAр)/Rbb. (5.24)
где Rpt — расчетное сопротивление полимерраствора на растяжение; Rb — призменная прочность бетона усиливаемой конструкции, соответствующая фактической кубиковой прочности; Aр — площадь поперечного сечения полимерраствора.
При совместном решении уравнений (5.23) и (5.24), учитывая, что Ар=bδp и исследуя полученное выражение на экстремум по δp, можно определить оптимальную высоту слоя полимерного покрытия из условия прочности
δр=[hRb-RsAs/2b·к(1+к)]/(Rb+Rр). (5.25)
Следует отметить, что наряду с увеличением прочности полимерные покрытия снижают деформативность изгибаемых элементов, особенно до появления трещин в бетоне. Наибольший эффект снижения деформативности происходит при нанесении покрытия по трем граням конструкции (боковым и растянутой) за счет перераспределения напряжений между покрытием и бетоном. Кроме этого полимерные покрытия, уплотняя поверхностную структуру бетона, частично устраняя очаги трещинообразования, воспринимая дополнительные напряжения, значительно повышают трещиностойкость железобетонных конструкций, что немаловажно при их эксплуатации в условиях агрессивного воздействия окружающей среды.
Момент трещинообразования таких конструкций определяют по формуле
Мcrc=кRbt,ser·Wpl, (5.26)
|где к = к1 + к2 — коэффициент упрочения бетона. При этом к1 — коэффициент, учитывающий упрочнение бетона от обжатия по-лимерраствором в процессе усадки; к2 - коэффициент, учитывающий упрочнение бетона полимерраствором; Rbt,ser – расчетное сопротивление бетона растяжению для предельных состояний второй группы; Wpt — момент сопротивления приведенного сечения, определяемый с учетом неупругих деформаций бетона и полимерраствора.
Wpt = Sbt+Ss+Sp+S1s, (5.27)
где Sbt, Ss, Sp, S1s — статические моменты площадей сечения соответственно растянутой зоны бетона, растянутой арматуры, полимерраствора и сжатой арматуры относительно нейтральной оси.
Более подробные сведения о расчете изгибаемых конструкций с полимеррастворными покрытиями по образованию трещин приведены в [34].
Расчет прочности, деформативности и трещиностойкости железобетонных изгибаемых конструкций, усиленных приклеиванием в растянутой зоне обычных или предварительно напряженных железобетонных элементов, выполняется по [50] как обычных монолитных, с увеличенным сечением бетона и арматуры (рис. 5.26, в). При расчете задаются толщиной приклеиваемого железобетонного элемента усиления. При наличии трещин в усиливаемой конструкции их необходимо перед усилением заинъецировать.
Площадь и диаметр требуемой арматуры в железобетонном элементе усиления определяют по формуле [33]
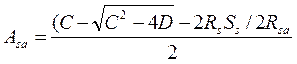 (5.28)
(5.28)
где C=RsсA1s+ Rb·b(2h+t); D=Rb·b [2МI max+Rs·As(2a+t)];
M1,max максимальное расчетное значение изгибающего момента от внешних сил и реакции опор, действующих на усиленную конструкцию; Rs, Rsa —расчетное сопротивление арматуры растяжению соответственно в усиливаемой конструкции и железобетонном элементе усиления, принимаемые по [50] и результатам испытаний вырезанных образцов; Rb — расчетное сопротивление бетона осевому сжатию (призменная прочность) усиливаемой конструкции, соответствующая фактической кубиковой прочности по результатам испытаний при проведении обследований; As, h, b — площадь растянутой арматуры, высота и ширина усиливаемой конструкции; а — расстояние от точки приложения равнодействующих усилий в арматуре As до растянутой грани сечения; t — толщина приклеиваемого железобетонного элемента усиления (см. рис. 5.26, в).
При определении максимального момента М1,max, действующего на усиленную конструкцию, необходимо учитывать собственниц вес приклеиваемого железобетонного элемента, предварительно задавшись его толщиной t.
Площадь требуемой арматуры по формуле (5.28) определяется методом последовательных приближений, варьируя толщиной приклеиваемого железобетонного элемента.
Полное использование прочностной характеристики арматуры элемента усиления обеспечивается подбором минимальной величины ее преднапряжения, с учетом всех потерь σsp2, по формуле
σsp2 = Ras+400-σsc,u 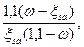 (5.29)
(5.29)
где σsc,u — предельное напряжение в арматуре сжатой зоны (п. 3.12 [50]; ω — характеристика сжатой зоны бетона (п. 3.12 1501); ξsa — относительная высота сжатой зоны, определяемая для арматуры элемента усиления ξsa = x/h0,sa, где х — высота сжатой зоны усиленной конструкции определяется из формулы
RsAs+RsaAsa-RscA1s = Rbbx; (5.30)
h0,sa — расстояние от сжатой грани усиленной конструкции до центра тяжести арматуры элемента усиления.
Подробные сведения о выборе конструктивного решения рассматриваемого способа усиления изгибаемых железобетонных элементов, расчете их по трещиностойкости и обеспечению совместной работы элемента усиления с усиливаемой конструкцией приведены в [33]. Там же приведена методика расчета изгибаемых железобетонных элементов усиливаемых стальными листами.
При расчете усиления балочных элементов, выполняемого путем постановки предварительно-напряженного шпренгеля, рассматривают комбинированную систему. Учитывая, что усиление балки выполняется тогда, когда к ней уже приложена основная нагрузка, выполняют приближенный расчет усиления как для балки, находящейся под воздействием заданной внешней нагрузки и усилий, передаваемых на балку со стороны шпренгеля (рис. 5.27, а), которые приравниваются к внешней нагрузке.
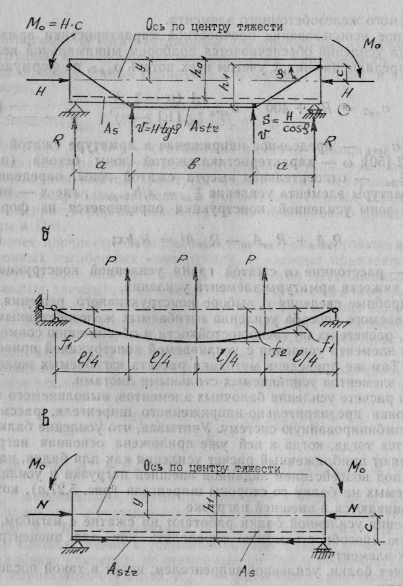
Рис. 5.27. Расчетная Схема балки: а — усиленной предварительно-напряженным шпренгелем; б — усиленной металлической балкой предварительно напрягаемой созданием начального прогиба; в — усиленной предварительно-напряженной горизонтальной затяжкой
Сечения усиленной балки работают на сжатие с изгибом, и их несущую способность можно определять как для внецентренносжатых элементов.
Расчет балки, усиленной шпренгелем, ведут в такой последовательности:
а) выбирают габариты шпренгеля а, b, с, h, φ, Astr;
б) определяют изгибающие моменты в пролете балки до и после усиления соответственно М и Мg;
в) назначают величину предварительного напряжения в шпренгельной затяжке σsp = 70/100 МПа;
г) определяют распор в шпренгеле в предельном состоянии по формуле
H = ( 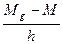 +σsp·Astr)·0,8≤0,8Rs,str·As,str, (5.31)
+σsp·Astr)·0,8≤0,8Rs,str·As,str, (5.31)
где 0,8 — коэффициент условий работы;
д) определяют усилия от шпренгеля в предельном состоянии
υ = Н·tgφ, М0 = Н·с; (5.32)
е) определяют расчетные усилия в системе в предельном состоянии
Mu = Мg+М0 — υ·a, Qu=R — υ; (5.33)
ж) проверяют сечения в усиленной балке от внецентренного сжатия в предельном состоянии на усилия:
Мu, N=H и Qu при е0=Мu/Н,
е=е0 + h0 — у, е1 = е0 + у — а1, (5.34)
где e0 — эксцентриситет относительно геометрической оси, проходящей по центру тяжести сечения.
При усилении изгибаемых элементов металлическими балками их устанавливают так, чтобы они эффективно выполняли свои функции. Для этого им сообщают предварительное напряжение путем создания начального прогиба. Величину прогиба определяют исходя из требуемой степени разгрузки. Металлическая балка стремясь выпрямиться будет разгружать усиливаемую железобетонную балку. Начальный расчетный прогиб создают с помощью устройства включающего домкрат и закрепляют прокладками [42]. При установке прокладок в трех сечениях балки пролетом 6 м прогиб в местах прокладок (см. рис. 5.27, б) может быть определен по следующим формулам
f1=2,18 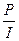 , f2=3,02
, f2=3,02 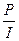 , (5.35)
, (5.35)
где f1 и f2 — соответствующие расчетные прогибы в местах установки прокладок; Р — требуемая сила разгрузки; I — момент инерции сечения металлической балки.
Определение несущей способности балки усиленной предварительно напряженной горизонтальной затяжкой может быть с достаточной для практики точностью произведено по формулам [50], если принять (рис. 5.27, в)
N = 0,85 Astr·Rs, (5.36)
где N — продольная сжимающая сила от преднапряженной затяжки; Astr — площадь сечения затяжки; 0,85 — коэффициент условий работы затяжки.
Опорные разгружающие моменты определяют из выражения
М0= Ne = N (h1 — у), (5.37)
где h1 — расстояние от затяжки до верхней грани усиливаемого элемента; у — расстояние от центра тяжести сечения балки до верхней ее грани.
Расчетный изгибающий момент М в пролете определяют по выражению
М = Мп — М0, (5.38)
где Мп — пролетный изгибающий момент от полной нагрузки, действующей на балку после усиления.
Эксцентриситет от центра тяжести сечения балки равен е0 = M/N соответственно эксцентриситеты от центра тяжести растянутой и сжатой арматуры
e=e0 + h0 — y, е1 = е0 — у+а1. (5.39)
Предварительное напряжение в затяжке, необходимое для включения ее в совместную работу с усиливаемой балкой, принимают в пределах σsp = 70 — 100 МПа.
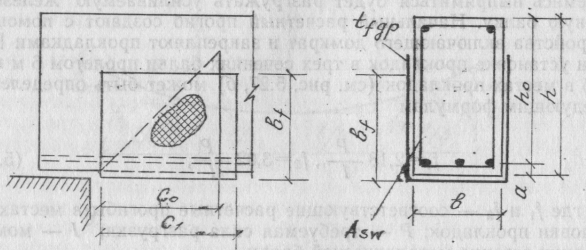
Рис. 5.28. Расчетная схема изгибаемого элемента,
усиленного на воздействие поперечных сил
Геометрические и прочностные характеристики поверхностно-оклеечного стеклопластика при усилении элементов по наклонным сечениям (рис. 5.28) определяются методом итерации из условия прочности на поперечную силу по формуле
Q ≤ (2 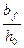 nfPf+
nfPf+ 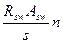 ) с0 +
) с0 + 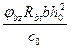 , (5.40)
, (5.40)
где Q — поперечная сила от внешних нагрузок, действующая на изгибаемый элемент после усиления; Rsw - расчетное сопротивление растяжению поперечной арматуры, принимаемое по [50]; Rbt — расчетное сопротивление бетона на растяжение; bf — ширина усиливаемой конструкции; h0 — рабочая высота сечения усиливаемой конструкции; Asw — площадь сечения одного стержня хомута; n — число хомутов или поперечных стержней в сечении усиливаемой конструкции; nfPf — см. п. 1 настоящего раздела и табл. 14[33]; s — шаг хомутов; φb2 — коэффициент, принимаемый но п. 3.31[50]; с0 — длина проекции наклонного сечения на продольную ось элемента, определяемая для усиливаемой конструкции по [50].
Геометрические параметры поверхностно-оклеечного стеклопластика, полученные по формуле (5.40) должны обеспечивать требуемую площадь приклейки стеклоткани в зависимости от среза бетона усиливаемой конструкции удовлетворять условию [34]
Q — Q1≤ 1,5RbtAf, (5.41)
где Q1 — поперечная сила от внешних нагрузок, действующая на изгибаемый элемент до усиления; Af — площадь поверхностно-оклеечного стеклопластика, определяемая согласно рис. 5.28 по формуле
Af = 2c1bf. (5.42)
3. Примеры расчета усиления железобетонных элементов
Пример 1. Требуется: запроектировать усиление колонны железобетонной обоймой, на которую после реконструкции будет действовать нагрузка N - 2000 кН (Nl = 1800 кН, Nsh=200 кН).
Первоначальное сечение колонны b×h = 30×30 см;
As = 12,56 см2 — 4Ø20 А—II; Rsc = 280 МПа; бетон класса В15;
Rb= 7,7 МПа; γb2=0,9; l0=5 м.
Решение: Принимается бетон обоймы класса В20 — Rb = 10,5 МПа; продольная арматура обоймы из стали класса A-III — Rsc,rcr = 365 МПа, поперечная арматура арматурного каркаса обоймы из стали класса А-1 в виде замкнутых хомутов, ηrcr = 0,8. Так как h = 300 мм > 200 мм, то ηb=1. Усиление колонны выполняется на всю высоту.
Принимаем толщину обоймы 60 мм, тогда гибкость усиленной колонны при =b+ 2d =30+2×6 = 42 см равна
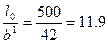
По табл. 5.1 при N1/N=1800/2000=0.884. φb=0.9φr=0.884
Определяем φ
φ=0.864+2 (0,884 - 0,864) 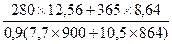 =0,882<φr = 0,884,
=0,882<φr = 0,884,
где As,rcr = 0,01 Arcr = 0,01 (42×42 — 30×30) = 8,64 см2. Площадь сечения бетона обоймы, армированной продольной арматурой с обычными вязаными хомутами
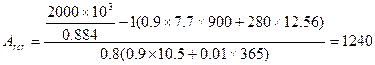 см2
см2
Находим требуемую толщину железобетонной обоймы по формуле
d = 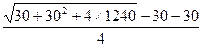 = 8,13 см
= 8,13 см
Принимаем толщину обоймы d = 8 см.
Определяем площадь сечения продольной арматуры обоймы по формуле
As,rcr= 0,01×1240 = 12,4 см2.
Принимаем 4Ø20 A-III с As,rcr = 12,56 см2.
Проверяем прочность сечения усиленной колонны
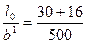 = 10,87, φb = 0,879, φr = 0,894,
= 10,87, φb = 0,879, φr = 0,894,
φ = 0,879+2 (0,894 - 0,879) 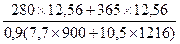 = 0,892 < φr= 0,894.
= 0,892 < φr= 0,894.
N = 2000×103H < 0,892 [ 1 (0,9×7,7×30×30 + 280×12,56) + 0,8 (0,9×10,5×1216 + 365×12,56)] × (100) = 2017100 Н — несущая способность усиленной колонны обеспечена.
Пример 2. Требуется: рассчитать усиление сборной железобетонной балки перекрытия пролетом 600 см и размерами поперечного сечения b×h = 25×50 см; балка запроектирована на нагрузку q = 50 кН/м, в том числе на постоянную нагрузку 23 кН/м; после замены оборудования нагрузка на балку должна возрасти до 70 кН/м.
Результатами проведенного обследования установлено, что геометрические размеры балки соответствуют проектным; признаки повреждений в балке отсутствуют; прочность бетона на сжатие соответствует условному классу В25; продольная арматура в растянутой зоне выполнена из 4Ø22 A-III (As = 15,2 см2), в сжатой зоне из 2Ø14 A-III (A1s = 3,08 см2), признаков коррозии арматуры нет; поперечные стержни арматурного каркаса из стали класса А-1 диаметром 8 мм при n = 2 (Asw = 0,503 см2) с шагом s = 20 см в крайних четвертях пролета и s = 30 см в средней части балки, защитный слой бетона снизу около 3 см (а = 3 см), сверху — 2,5 см (a1≈3 см); h0 = 47 см.
Решение: так как бетон и арматура балки не имеют повреждений, то поверочный расчет выполняем по предельным состояниям, принимая расчетные сопротивления бетона и арматуры [50]: Rb = 14,5 МПа, Rbt = 1,05 МПа, Rs = Rsc=365 МПа, Rsw = 175 МПа, γb2 = 0.9, ξR=0,551.
Определяем несущую способность балки по моменту и поперечной силе [М] = γb2Rb·b·x(h0 — 0,5 x) + RscA1s(h0 — а1);
x= 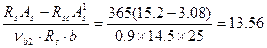 см;
см;
ξ= 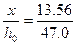 =0,288<ξR=0.551;
=0,288<ξR=0.551;
[М] = 0,9 (100) 14,5×25×13,56 (47,0 — 0,5×13,56) = (100) 365×2,26 (47,0 — 3,0) = 22739606 Н·см = 227,4 кН·м
[Q] = Qb+Qsw,
Qb= 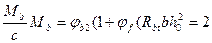 ×1×1.05 (100) 25×472 = 11597200 Н·см = 115,97кН·м,
×1×1.05 (100) 25×472 = 11597200 Н·см = 115,97кН·м,
с = 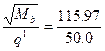 = 1,52 м, где q1 = q = 50,0 кН/м ≈ 0,56 qsw = 49,28 кН/м;
= 1,52 м, где q1 = q = 50,0 кН/м ≈ 0,56 qsw = 49,28 кН/м;
Qb = 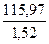 =76,3 кН > Qb,min=74,0 кН;
=76,3 кН > Qb,min=74,0 кН;
Qb,min = φb3(1 + φf) Rbt·b·h0=0.6×1,05 (100) 25×47 = 74020 H = 74,0 кН.
Qsw = qsw·c0, где c0 = 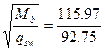 = 1,12 м,
= 1,12 м,
qsw= 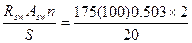 =927,5 H/см = 92,75 кН/м.
=927,5 H/см = 92,75 кН/м.
с = 1,52 м > с0 = 1,12 м > 2h0 = 0,94 м, принимаем
с0 = 2h0 = 0,94 м, тогда
Qsw = 92,75×0,94 = 87,2 кН,
[Q] = 76,3 + 87,2 = 163,5 кН.
При существующей нагрузке
Mmax 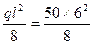 = 225,0 кН·м,
= 225,0 кН·м,
Qmax = 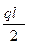 =50×3 = 150 кН.
=50×3 = 150 кН.
Таким образом до реконструкции удовлетворялись условия прочности как по М, так и по Q:
[М] > Mmax, [Q] > Qmax
После реконструкции максимальный изгибающий момент и максимальная поперечная сила будут соответственно равны
Мmax = 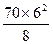 =315,0 кН·м, Qmax = 70 × 3 = 210,0 кН.
=315,0 кН·м, Qmax = 70 × 3 = 210,0 кН.
Дата добавления: 2016-01-26; просмотров: 1426;
