Доказательство достаточности.
I группа. Простейшее: 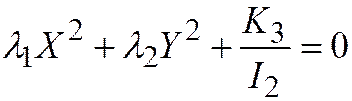 .
.
1. Если 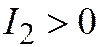 ,
, 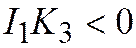 , то корни
, то корни 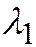 и
и 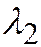 характеристического уравнения
характеристического уравнения 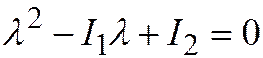 имеют одинаковые знаки (т.к.
имеют одинаковые знаки (т.к. 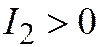 , а
, а 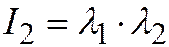 ). Далее, т.к.
). Далее, т.к. 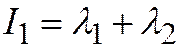 , то знак
, то знак 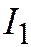 одинаков со знаками
одинаков со знаками 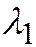 и
и 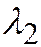 , а т.к.
, а т.к. 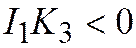 , то
, то 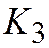 имеет знак им противоположный. Отсюда следует, что простейшее уравнение
имеет знак им противоположный. Отсюда следует, что простейшее уравнение 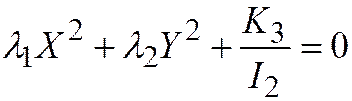 приводится к виду:
приводится к виду: 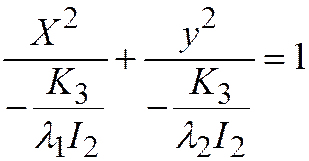 .
. 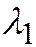 берётся наименьшим по абсолютной величине. Теперь, т.к.
берётся наименьшим по абсолютной величине. Теперь, т.к. 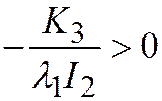 ;
;  , то уравнение
, то уравнение 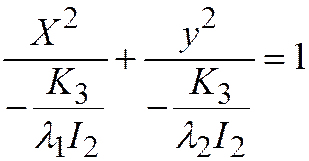 является каноническим уравнением эллипса с полуосями:
является каноническим уравнением эллипса с полуосями: 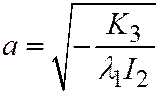 ,
, 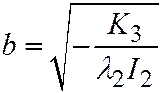 .
.
2. Если 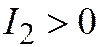 ,
, 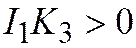 , то
, то 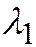 ,
, 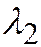 и
и 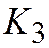 имеют одинаковые знаки и значит, простейшее уравнение
имеют одинаковые знаки и значит, простейшее уравнение 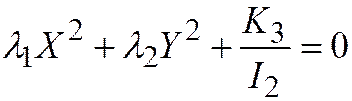 приводится к виду:
приводится к виду: 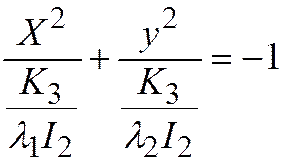 и будет являться уравнением мнимого эллипса
и будет являться уравнением мнимого эллипса 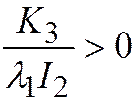 ;
; 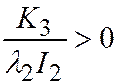 .
.
3. Если 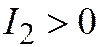 ,
, 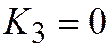 , то простейшее уравнение
, то простейшее уравнение 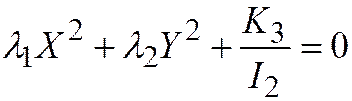 принимает вид:
принимает вид: 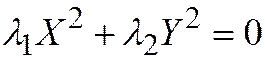 , причём
, причём 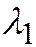 и
и 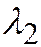 в силу условия
в силу условия 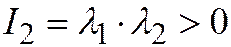 имеют одинаковые знаки; то последнее уравнение можно переписать в виде:
имеют одинаковые знаки; то последнее уравнение можно переписать в виде: 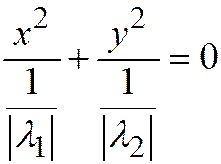 или
или 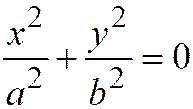 , где
, где 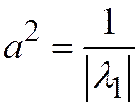 ,
, 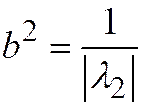 . Таким образом, мы пришли к уравнению двух мнимых пересекающихся прямых.
. Таким образом, мы пришли к уравнению двух мнимых пересекающихся прямых.
4. Если 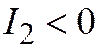 ,
, 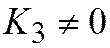 , то
, то 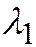 и
и 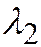 разных знаков. Обозначим через
разных знаков. Обозначим через 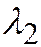 тот из корней характеристического уравнения, который имеет знак, противоположный знаку
тот из корней характеристического уравнения, который имеет знак, противоположный знаку 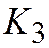 , и перепишем простейшее уравнение
, и перепишем простейшее уравнение 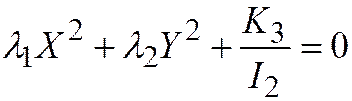 так:
так: 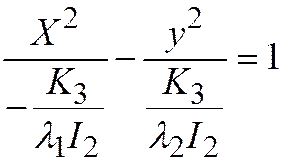 . Здесь
. Здесь 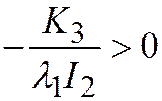 ,
, 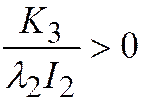 и, полагая
и, полагая 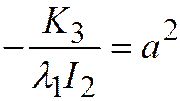 ;
; 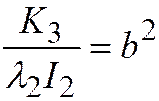 получаем каноническое уравнение гиперболы:
получаем каноническое уравнение гиперболы: 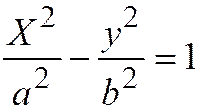 .
.
5. Если 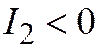 ,
, 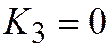 , то простейшее уравнение
, то простейшее уравнение 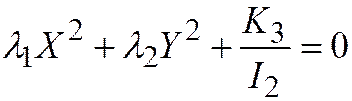 принимает вид:
принимает вид: 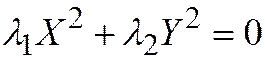 . Здесь
. Здесь 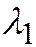 и
и 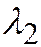 разных знаков (т.к.
разных знаков (т.к. 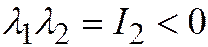 ). Считая
). Считая 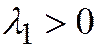 ,
, 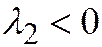 , запишем это уравнение в виде:
, запишем это уравнение в виде: 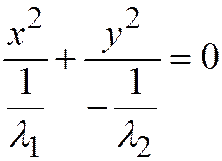 или
или 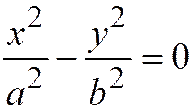 , где
, где 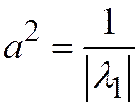 ,
, 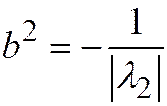 . Таким образом, мы пришли к уравнению двух пересекающихся прямых.
. Таким образом, мы пришли к уравнению двух пересекающихся прямых.
6. Если 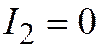 ,
, 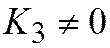 , то простейшее уравнение
, то простейшее уравнение 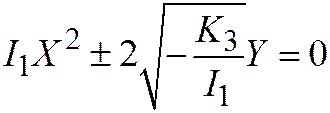 является уравнением параболы.
является уравнением параболы.
7. Если 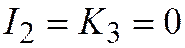 , то простейшее уравнение имеет вид:
, то простейшее уравнение имеет вид: 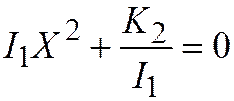 или
или 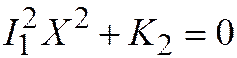 . Отсюда следует, что если
. Отсюда следует, что если 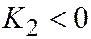 , то уравнение является уравнением двух параллельных прямых, если
, то уравнение является уравнением двух параллельных прямых, если 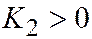 - то уравнением двух мнимых параллельных прямых, а если
- то уравнением двух мнимых параллельных прямых, а если 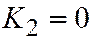 - то уравнением двух совпадающих прямых. Достаточность доказана.
- то уравнением двух совпадающих прямых. Достаточность доказана.
Доказательство необходимости проводится методом от противного. Пусть, например, общее уравнение линии второго порядка, заданное относительно ДПСК, является уравнением эллипса; требуется доказать, что 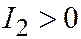 ,
, 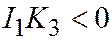 . Полагая
. Полагая 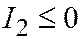 , заключаем, что данное уравнение является уравнением одной из линий
, заключаем, что данное уравнение является уравнением одной из линий  , указанных в нашей таблице.
, указанных в нашей таблице.
Итак, 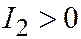 . Предполагая, что
. Предполагая, что 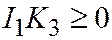 , заключаем, что данное уравнение является либо уравнением мнимого эллипса, либо уравнением двух мнимых пересекающихся прямых. Значит,
, заключаем, что данное уравнение является либо уравнением мнимого эллипса, либо уравнением двух мнимых пересекающихся прямых. Значит, 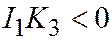 .
.
Аналогично, методом от противного c использованием доказанной достаточности признаков, указанных в последней таблице, доказывается необходимость всех этих признаков.
Следствие. Для того, чтобы линия второго порядка, заданная общим уравнением 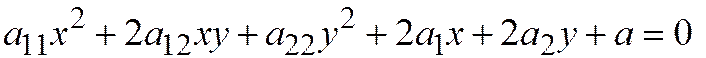 относительно ДПСК распадалась на две прямые, необходимо и достаточно, чтобы выполнялось равенство:
относительно ДПСК распадалась на две прямые, необходимо и достаточно, чтобы выполнялось равенство: 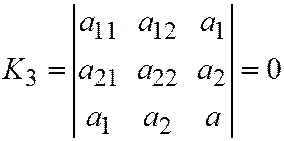 .
.
Доказательство. Из доказанной теоремы 3 следует, что если для линии I группы 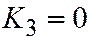 , то соответствующее уравнение
, то соответствующее уравнение 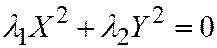 является уравнением двух прямых, а если
является уравнением двух прямых, а если 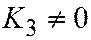 , то уравнение линии I группы не является уравнением двух прямых. Для параболы (группа II)
, то уравнение линии I группы не является уравнением двух прямых. Для параболы (группа II) 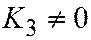 , а для всех линий второго порядка III группы, каждая из которых распадается на две прямые,
, а для всех линий второго порядка III группы, каждая из которых распадается на две прямые, 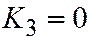 . Следствие доказано.
. Следствие доказано.
Для решения задач, давайте запомним формулу для определения центра линии второго порядка, которую чуть позже мы докажем. Центр 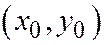 линии второго порядка заданной относительно ДПСК общим уравнением
линии второго порядка заданной относительно ДПСК общим уравнением 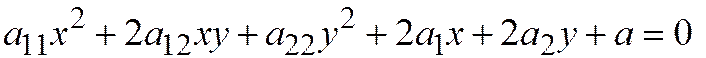
определяется из следующей системы уравнений: 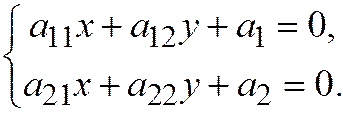
| <== предыдущая лекция | | | следующая лекция ==> |
| | |
Дата добавления: 2016-01-20; просмотров: 742;
