Эллипс, гипербола и парабола как конические сечения.

Рассмотрим поверхность прямого кругового конуса, неограниченно простирающегося по обе стороны от его вершины.

Плоскость, проходящая через вершину конуса может занимать относительно этого конуса следующие три положения:

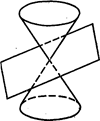
1) Иметь с конусом только одну общую точку (вершину конуса (См. рис.187)).

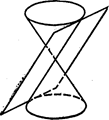
2) Касаться конуса вдоль его образующей (См. рис.188).

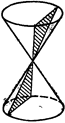
3) Пересекать конус по двум различным его образующим (См. рис.189).

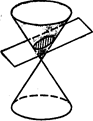
Плоскость, не проходящая через вершину конуса, может занимать относительно конуса также три различных положения: 1) Пересекать все образующие конуса (См.рис.190)

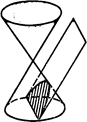
2) Быть параллельной только одной образующей конуса (См. рис.191).

3) Быть параллельной двум различным образующим конуса (См. рис.192).

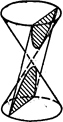
Теорема 2. Плоскость, не проходящая через вершину прямого кругового конуса, пересекает его по эллипсу, если она пересекает все образующие конуса (См. рис.190), по параболе, если она параллельна только одной образующей конуса (См. рис.191) и по гиперболе, если она параллельна двум образующим конуса (См. рис.192).

Доказательство. Для доказательства рассмотрим прямой круговой конус, который в прямоугольной системе координат 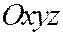описывается уравнением:

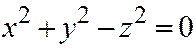(6)

и геометрически получается при вращении вокруг оси 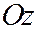прямой 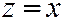, принадлежащей координатной плос-кости 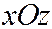. В силу круговой симметрии поверхности (6) можно ограничиться только сечениями при помо-щи плоскостей, перпендикулярных координатной пло-скости 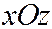. Таким плоскостям соответствуют уравнения , .

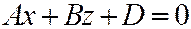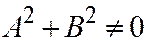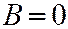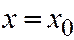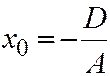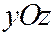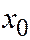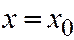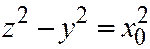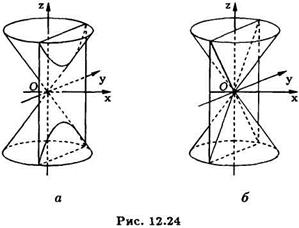
Если , то секущая плоскость описывается уравнением , где и параллельна координатной плоскости . Подставив значение абсциссы в уравнение конуса (6), найдём, что сечение в плоскости описывается уравнением и при 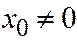определяет собой равностороннюю гиперболу (См. рис.12.24), а при 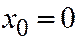пару прямых, которые являются образующими конусам. Рис.12.24.

Пусть теперь в уравнении секущей плоскости коэффициент 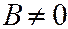. Тогда плоскость можно представить уравнением 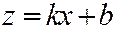, где 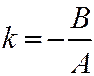, 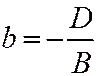. В силу симметрии конуса относительно плоскости 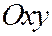достаточно ограничиться случаем, когда .

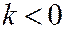Коническое сечение для рассматриваемой плоскости в пространстве будет описываться системой двух уравнений 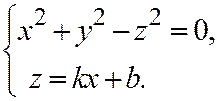(7)

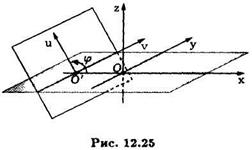
Чтобы получить уравнение секущей плоскости, рассмотрим прямоугольную систему координат ,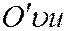

взяв в качестве координатных осе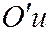й и 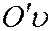прямые, являющиеся пересечением секущей плоскости с координатными плоскостям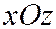и и 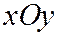(См.рис. 12.25 ).

Координаты 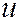и 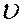произвольной точки в секущей плоскости будут связаны с её координатам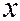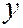и , и 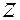в пространстве соотношениями:

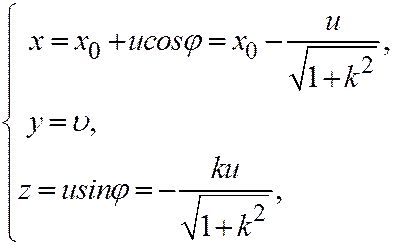(8)

где 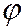- угол между коническим сечением, перпендикулярным координатной плоскости 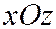, и координатной плоскостью 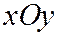, причём 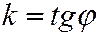, а .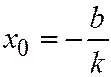

Подставляя (8) в первое уравнение системы (7), т.е. в уравнение 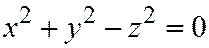, получим уравнение конического сечения в системе координат :

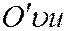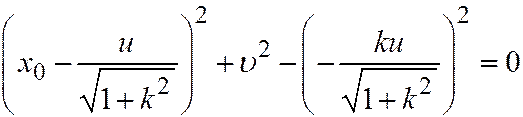. Раскрывая скобки и приводя подобные члены, находим:

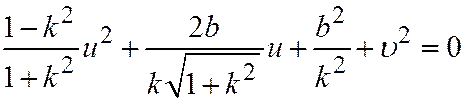. (9)

При 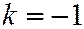, когда секущая плоскость образует с плоскостью 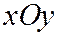тот же угол, что и образующие конуса, конические сечения будут представлять собой параболы (См. рис. ) и описываться уравнением:

.

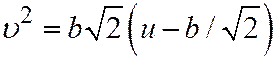Варьируя параметр 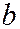в уравнении секущей плоскости, в качестве конического сечения можно получить любую параболу.

При 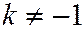, 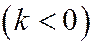уравнение (9) принимает вид:

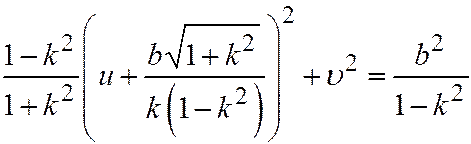. (10)

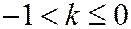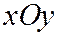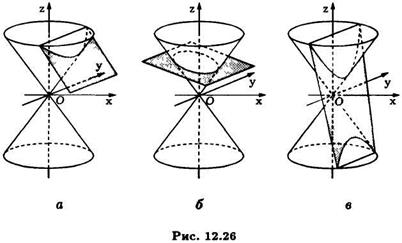
Здесь возможны два варианта. При , т.е. когда секущая образует с плоскостью меньший угол, чем образующие конуса, будет выполнено неравенство 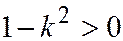и поэтому уравнение (10) конического сечения будет уравнением эллипса (См. рис. 12.26).

И здесь варьируя параметры 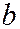и 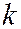в уравнении секущей плоскости, мы можем получить в сечении любой эллипс.

При 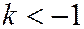, т.е. когда секущая плоскость образует с плоскостью 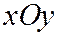больший угол, чем образующие конуса, имеем 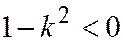, так что коническое сечение, описываемое уравнением (10) будет являться гиперболой (См. рис. ). Варьируя параметры 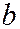и 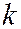можно получить в коническом сечении любую гиперболу.